2.2. Закон Біо і Савара-Лапласа

Магнітна індукція в будь-якій точці поля навколо провідника з електричним струмом визначається за законом Біо і Савара-Лапласа.

Закон Біо і Савара-Лапласа: будь-який елемент провідника довжиною dℓ зі струмом  створює в точці А на відстані  від елемента провідника магнітне поле, магнітна індукція  якого прямо пропорційна довжині елемента dℓ, величині струму І, синусу кута α між напрямом струму та радіус-вектором, що з’єднує даний елемент із точкою поля, та обернено пропорційна квадрату довжини радіус-вектора (рис. 2.3). Математично закон Біо і Савара-Лапласа записується наступним чином:

.                                        (2.9)

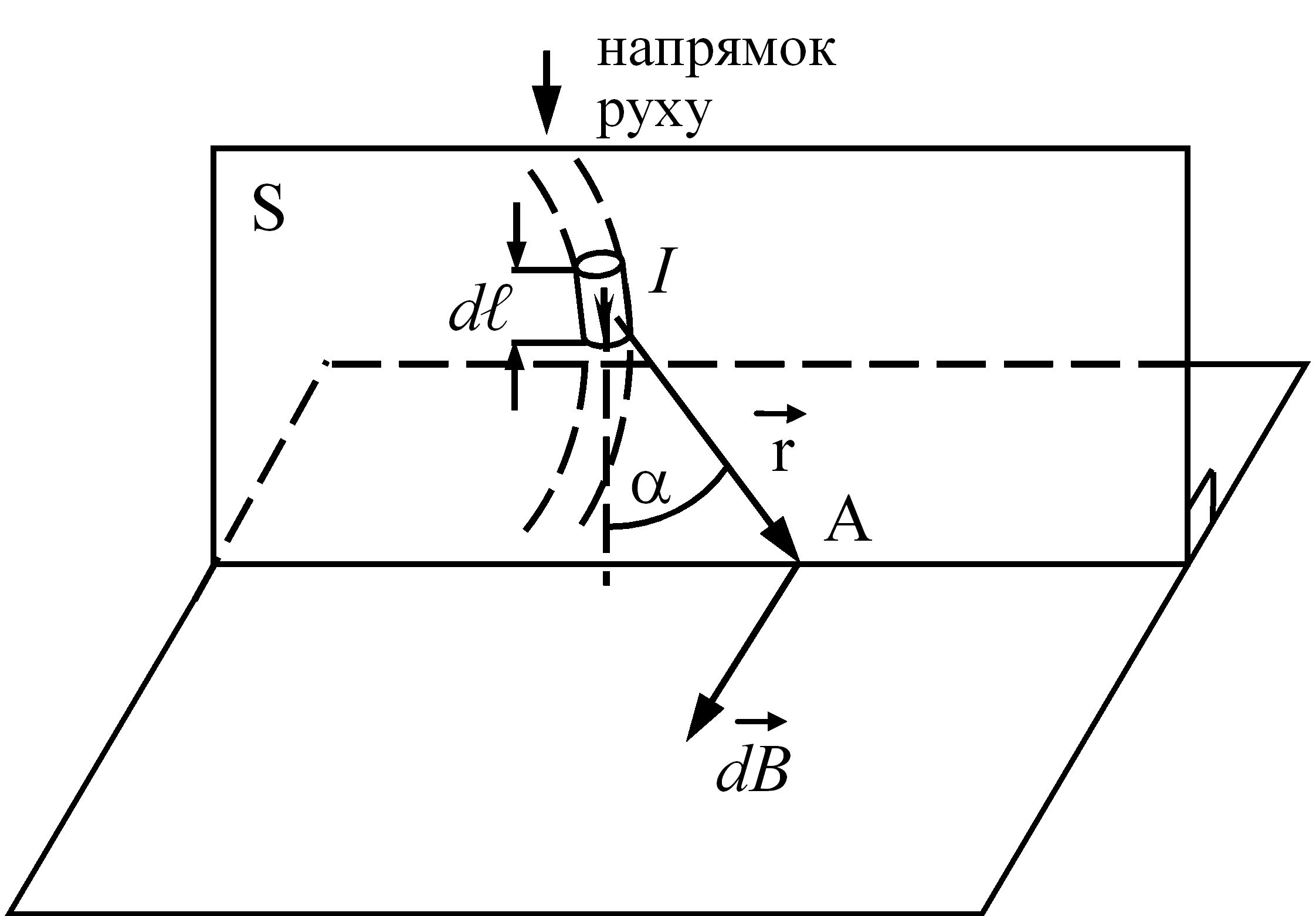
Рис. 2.3 – Пояснення до визначення закону Біо і Савара-Лапласа

Вектор  направлений перпендикулярно площі S, в якій розташовано радіус-вектор  та елемент dℓ. Напрямок вектора  визначається за правилом буравчика: якщо буравчик рухається вздовж елемента провідника за напрямом струму, то один кінець його рукоятки проходить крізь площину S у тому ж напрямку, в якому її пронизує вектор ; при цьому точка, в якій цей кінець рукоятки проходить крізь площу S, повинна знаходитися з того ж боку елемента  dℓ, що й точка А.

Струм проходить не по окремих елементах провідника  dℓ, а по цільному провіднику визначеної конфігурації. Тому вектор магнітної індукції у будь-якій точці визначається за формулою

.                                        (2.10)

Для ілюстрації застосування закону Біо і Савара-Лапласа визначимо магнітну індукцію в центрі кільцевого провідника зі струмом (рис. 2.4).

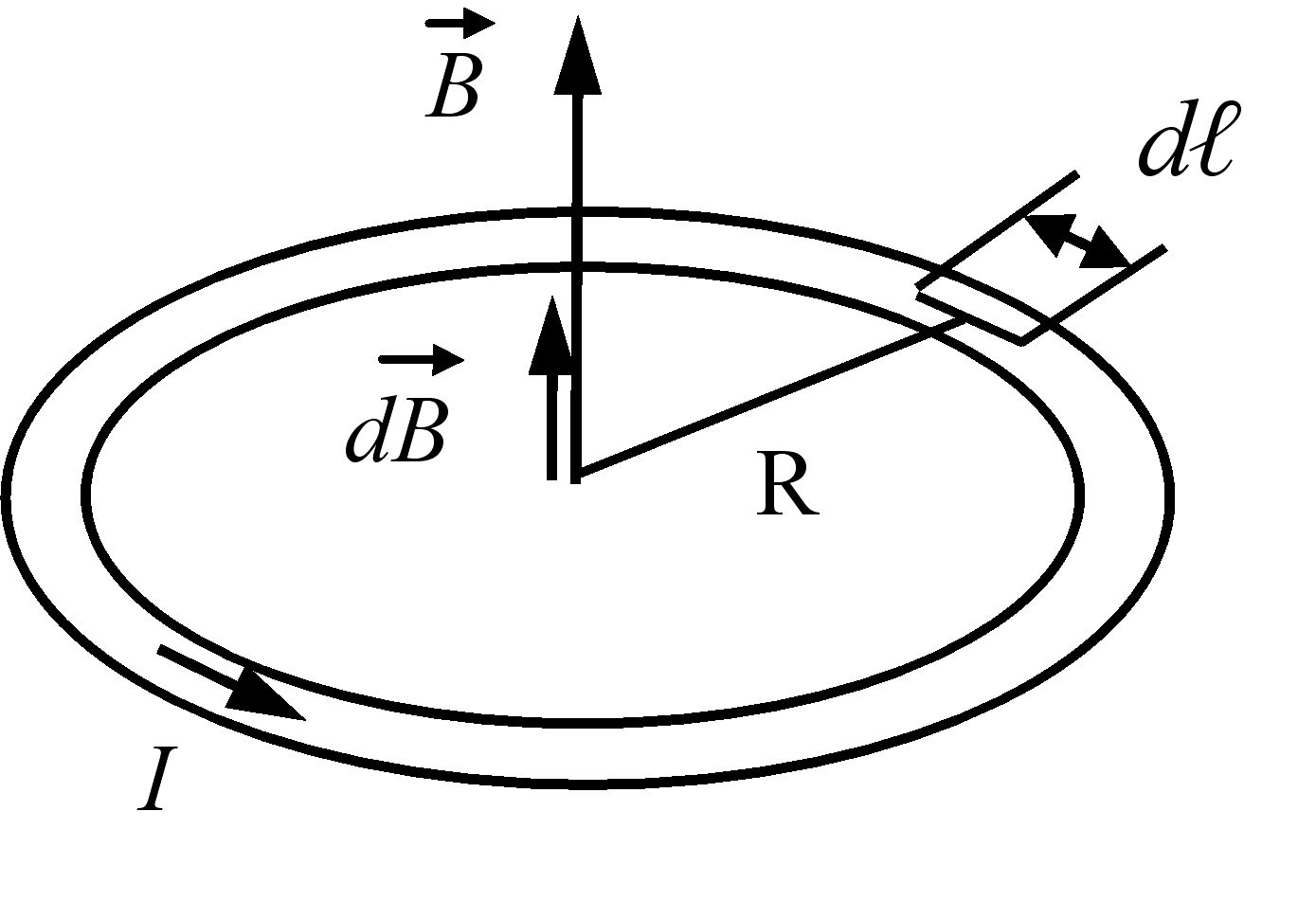
Рис. 2.4 – Магнітна індукція кільцевого провідника зі струмом

Радіус-вектор  за довжиною дорівнює радіусу кільця R, , . Застосовуємо закон Біо і Савара-Лапласа (2.9):

.

За формулою (2.10) визначаємо магнітну індукцію в центрі кільця:

,

де знак означає інтегрування по замкненому контуру: . Остаточно:

.                        (2.11)