3.3. Способи подання синусоїдальних величин

Існує декілька способів математичного подання синусоїдальних величин.

Аналітична форма. Синусоїдальна величина подається за допомогою тригонометричної функції. Наприклад, сила електричного суму: 

                                              (3.10)

У деяких випадках можливе додавання (віднімання) синусоїдальних величин в аналітичній формі за допомогою тригонометричних формул.

Приклад: додати дві синусоїдальні величини i1  та i2  однакової амплітуди та частоти, але з різними початковими фазами (0 та ):

Одержуємо:

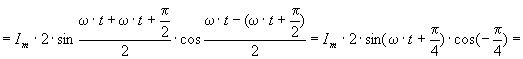
За допомогою часових діаграм. У визначеному масштабі по осі абсцис відкладаються проміжки часу від початку відліку часу, по осі ординат – миттєві значення синусоїдальної величини (рис. 3.4).

Таке подання дає можливість геометрично визначити амплітуду, початкову фазу і період синусоїдальної величини.

Додавання (віднімання) двох синусоїдальних величин можна виконати графічно шляхом додавання (віднімання) двох синусоїд, що зображують ці величини. Для одержання ординат сумарної кривої потрібно для кожного моменту часу додати ординати кривих. Це виконано на рис. 3.5 для прикладу з вихідними умовами, розглянутими на початку цього параграфа.

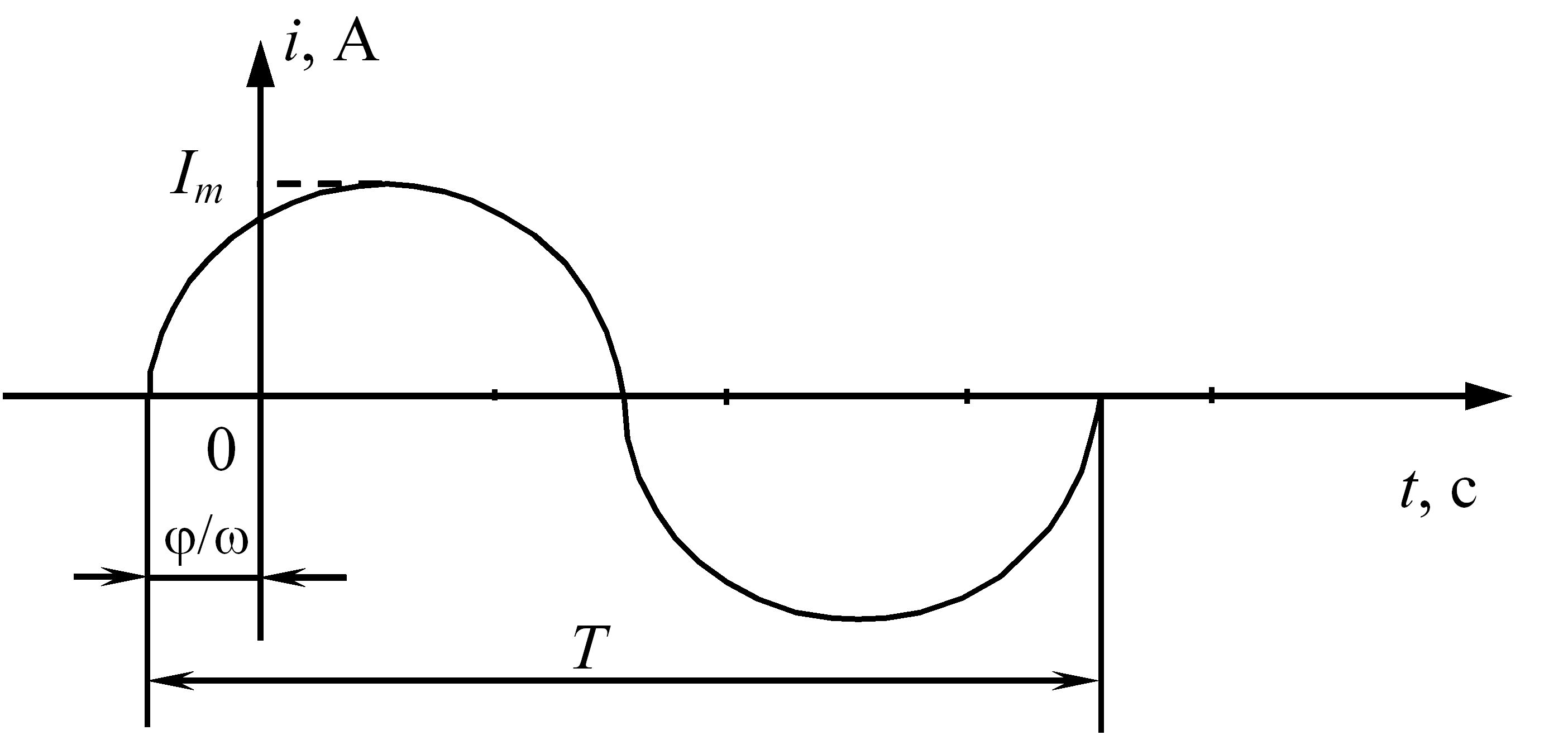
Рис. 3.4 – Часова діаграма синусоїдального змінного струму

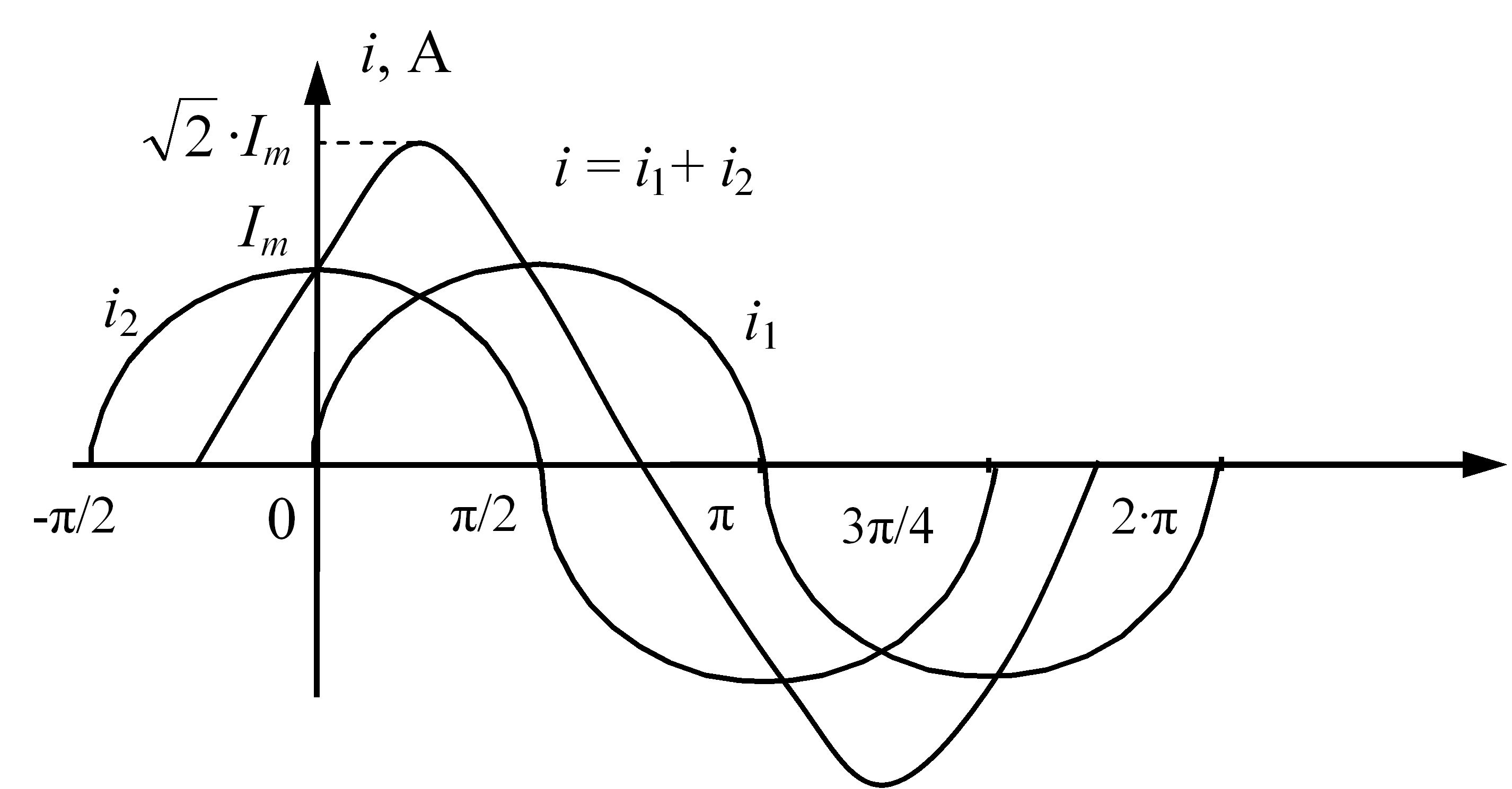
Рис. 3.5 – Додавання синусоїдальних величин, поданих у вигляді часових діаграм

Графічно додавати (віднімати) можна синусоїдальні величини будь-якої частоти, амплітуди і початкової фази. При додаванні двох синусоїдальних величин однакової частоти створюється синусоїдальна величина тієї ж частоти. При додаванні двох синусоїдальних величин різної частоти створюється несинусоїдальна величина.

Векторна форма. Відомо, що вектор характеризується довжиною та напрямком. Синусоїдальна величина може зображуватися вектором, що обертається. Довжина вектора в масштабі дорівнює амплітуді синусоїдальної величини (або діючому значенню синусоїдальної величини). За нульовий напрямок вектора (нульовий кут) обирається напрямок на три години за циферблатом годинника. За позитивний напрямок обертання вибирається напрямок обертання вектора проти годинникової стрілки. Кут, створений вектором із нульовим напрямком у початковий момент часу, дорівнює початковій фазі. Швидкість обертання вектора дорівнює кутовій частоті. Миттєві значення синусоїдальної величини виражаються проекціями вектора на вісь ординат. 

Векторною діаграмою називається сукупність векторів, що зображують декілька синусоїдальних величин однакової частоти в початковий момент часу.

Додавання (віднімання) двох синусоїдальних величин можна проводити у векторній формі. При цьому додавання (віднімання) векторів виконують за відомими геометричними правилами (правило трикутника, правило паралелограма).

На рис. 3.6 виконаний приклад векторного додавання двох синусоїдальних величин із вихідними умовами, розглянутими на початку цього параграфа.

Рис. 3.6 – Приклад додавання синусоїдальних величин, поданих у векторній формі

З геометричних міркувань довжина результуючого вектора дорівнює 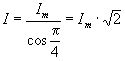, початкова фаза – .

Символічний метод (за допомогою комплексних величин). Величина (сила) постійного електричного струму визначається одним числом. Величина (сила) змінного електричного струму заданої частоти визначається двома числами: амплітудою і початковою фазою. Величина (сила) змінного електричного струму може бути подана одним числом – комплексним. 

Комплексність величини A в електротехніці позначається  (загальне позначення) або  (для діючих або амплітудних значень величин, що є синусоїдальною функцією часу). 

З вищої математики відомо, що комплексним числом  називається сума дійсного числа А' та уявного числа (квадратний корінь з негативного числа, наприклад,  ). Уявне число  подають у вигляді добутку дійсного числа A" та квадратного кореня з негативної одиниці , який називають "уявною одиницею" і позначають у вищій математиці – літерою "i", а в електротехніці – літерою "j":

.                                          (3.11)

Існує три форми подання комплексних чисел:

– алгебраїчна: ;

– тригонометрична: , де – модуль комплексного числа,  – фаза комплексного числа;

– показова: 

Комплексні числа додаються, віднімаються, множаться, діляться за правилами, відомими із вищої математики. 

Розглянемо приклад додавання двох комплексних величин, що описують синусоїдальні величини з вихідними умовами, розглянутими на початку цього параграфа.

Сила струму з нульовою початковою фазою  у комплексній формі має вид: . Як правило, модулем комплексного струму вважають його дійсне значення. 

Сила струму  i1  додається до сили струму i2 із тією самою амплітудою, частотою, але з початковою фазою : .

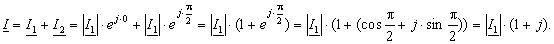
Миттєве значення результуючої сили струму:

.

Зображення синусоїдальних величин комплексними числами дозволяє значно спростити розрахунки електричних кіл змінного струму. У цьому випадку говорять, що електричні кола розраховуються символічним методом.