ЕЛЕКТРОТЕХНІКА ТА ПОЖЕЖНА ПРОФІЛАКТИКА В ЕЛЕКТРОУСТАНОВКАХ - 3.5. Види опорів у електричних колах змінного струму

3.5. Види опорів у електричних колах змінного струму

Електричне коло з резистивним елементом. Розглянемо електричне коло змінного струму з одним резистивним елементом з активним опором r (рис. 3.11), затискачі якого підключено до джерела синусоїдальної напруги:

. (3.23)

Рис. 3.11 – Електричне коло змінного струму з резистивним елементом

Сила струму у колі визначається за законом Ома. Для миттєвих значень:

. (3.24)

З останньої формули можна зробити висновок, що у колі сила струму і напруга збігаються за фазою.

Розділивши праву і ліву частини виразу на , одержимо закон Ома для діючих значень для електричного кола змінного струму з резистивним елементом:

. (3.25)

На рис. 3.12 приведено часову діаграму сили струму і напруги для електричного кола змінного струму з резистивним елементом.

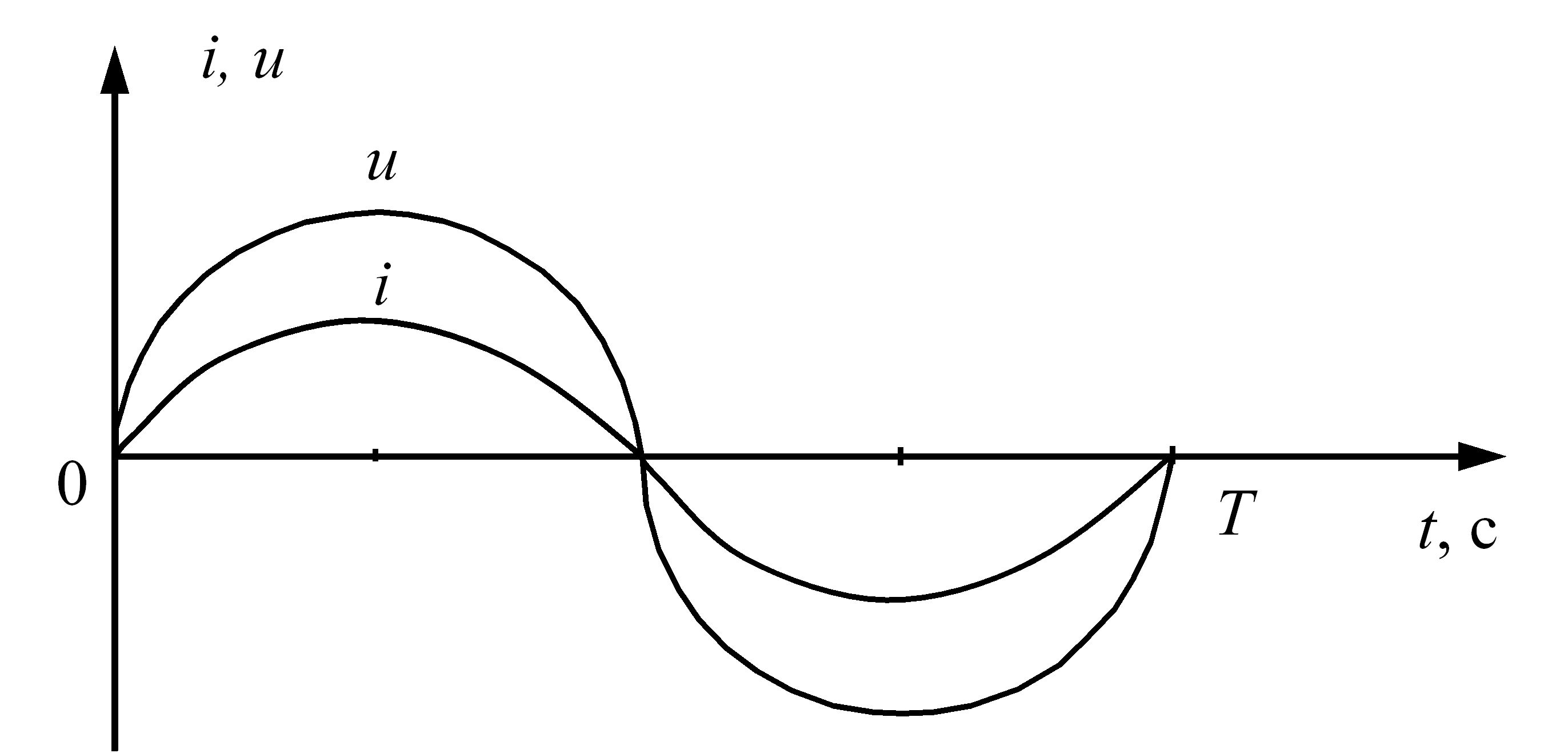
Рис. 3.12 – Часова діаграма сили струму і напруги для електричного кола змінного струму з резистивним елементом

Векторна діаграма сили струму і напруги для електричного кола змінного струму з резистивним елементом приведена на рис. 3.13.

Рис. 3.13 – Векторна діаграма сили струму і напруги для електричного кола змінного струму з резистивним елементом

Активний опір змінному струму резистивного елемента завжди є дещо більшим за активний опір постійному струму того ж резистивного елемента. Це пояснюється тим, що змінний струм частково витісняється від центру провідника, з якого виготовлений резистивний елемент, до його зовнішньої поверхні (поверхневий ефект або "скін-ефект"). Це призводить до неповного використання перерізу провідника – він ніби зменшується, а отже, опір провідника збільшується.

Визначимо потужність кола змінного струму з резистивним елементом.

Миттєва потужність (позначається латинською літерою p, [Вт]) – фізична величина, що дорівнює добутку миттєвого значення напруги і миттєвого значення сили струму та характеризує швидкість перетворення електричної енергії в інший вид енергії у визначений момент часу. Для резистивного елемента:

. (3.26)

З виразу (3.26) випливає, що миттєва потужність у резистивному елементі дорівнює сумі двох величин: постійної U·I і змінної (-U·I·cos(2·ω·t)), що змінюється в часі з подвійною частотою ω.

Часова діаграма миттєвої потужності для електричного кола змінного струму з резистивним елементом приведена рис. 3.14.

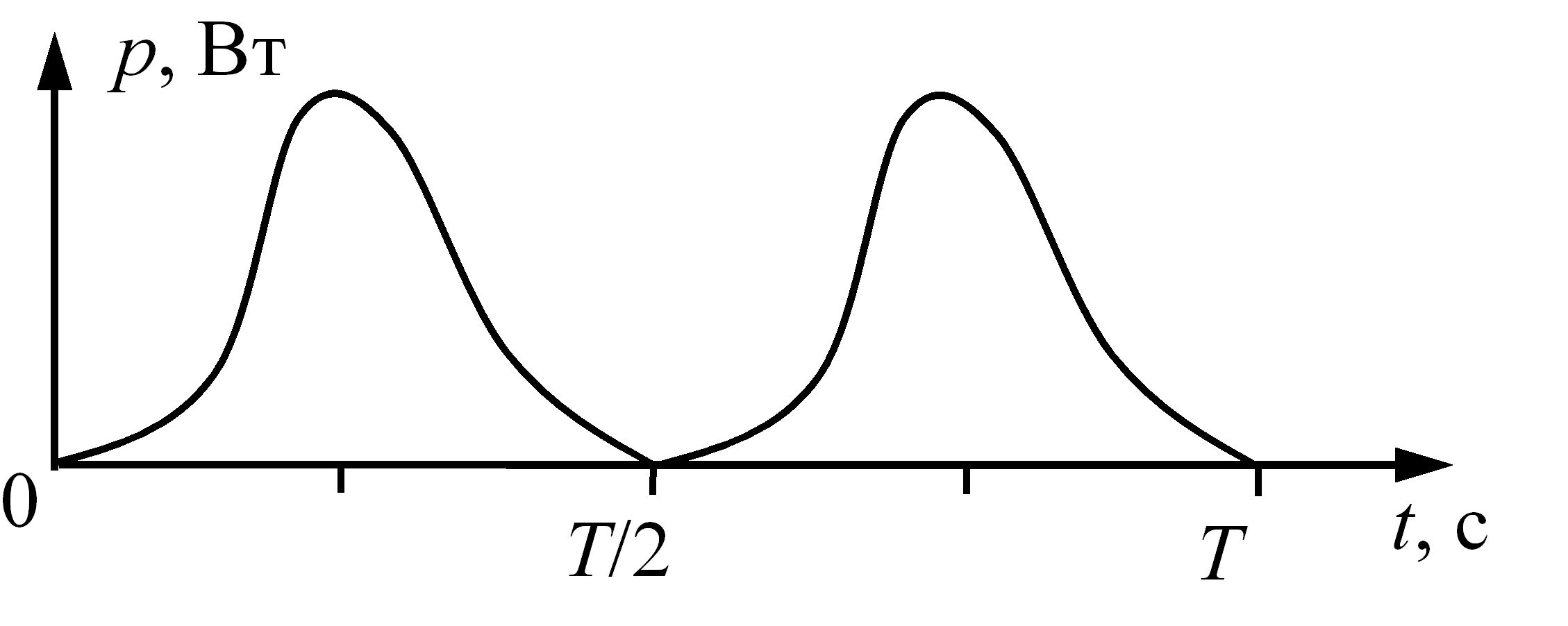
Рис. 3.14 – Часова діаграма миттєвої потужності для електричного кола змінного струму з резистивним елементом

Потужність є позитивною як при i>0, так і при i<0 тому, що електрична енергія перетворюється в теплову енергію незалежно від напрямку струму в колі.

Активна потужність (позначається латинською літерою Р, [Вт]) – фізична величина, що дорівнює середній за період миттєвій потужності та характеризує середню швидкість перетворення електричної енергії в інший вид енергії (в електричному колі з резистивним елементом – у теплову енергію). Математично активна потужність для резистивного елемента визначається за формулою:

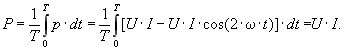(3.27)

Величина активного опору резистивного елемента визначає разом із напругою мережі величину струму, що проходить по провідниках. Відповідно до закону Джоуля-Ленца, сила струму й активний опір кола визначають кількість тепла, що виділяється у провіднику при проходженні по ньому електричного струму. Дане явище застосовується в електротермічних установках. При порушенні правил їх експлуатації ці установки можуть стати причиною пожежі.

Електричне коло з індуктивним елементом. Розглянемо електричне коло змінного струму з індуктивним елементом (ідеальною котушкою індуктивності) з індуктивністю величиною L, затискачі якого підключено до джерела синусоїдальної напруги u (рис. 3.15).

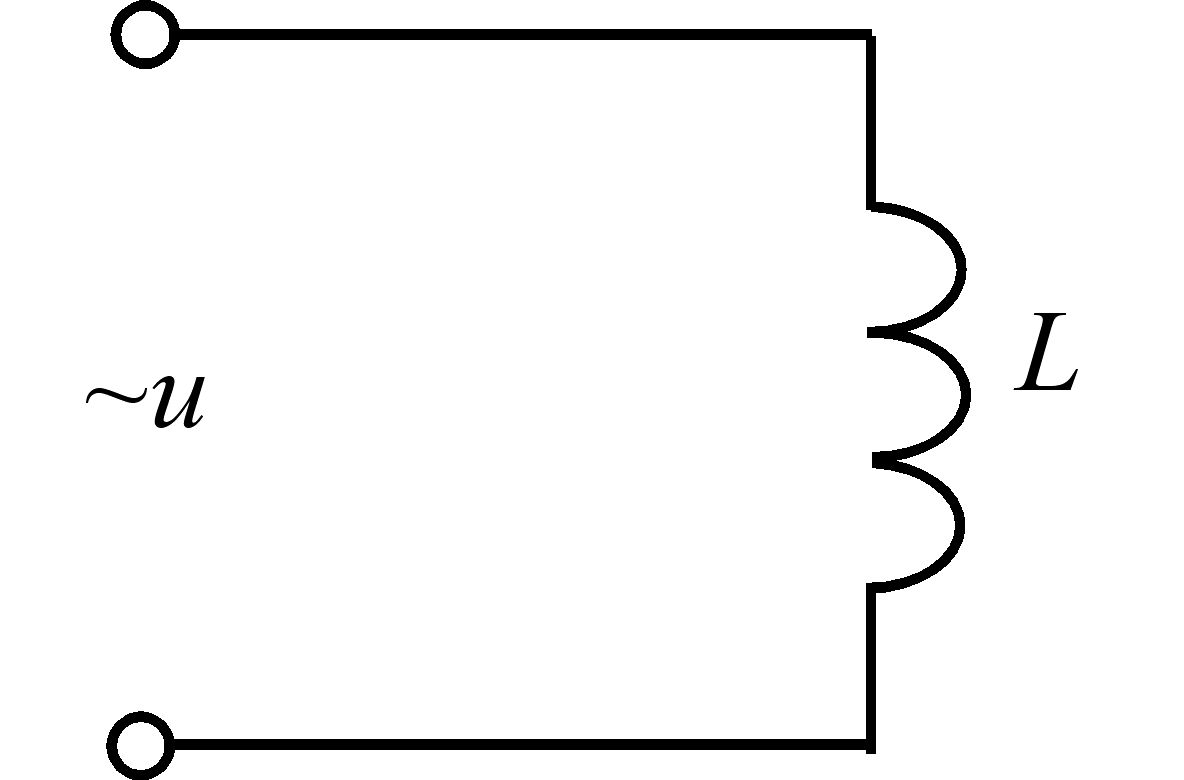
Рис. 3.15 – Електричне коло змінного струму з індуктивним елементом

Під дією прикладеної синусоїдальної напруги u у колі існує змінний струм:

, (3.28)

який створює змінний магнітний потік:

Цей змінний потік наводить у індуктивному елементі електричного кола ЕРС самоіндукції:

(3.29)

де позначено ELm= L· Im· ω.

За другим законом Кірхгофа для електричного кола сума прикладеної до кола напруги джерела живлення u і ЕРС самоіндукції eL дорівнює нулю: u + eL = 0. Тоді

(3.30)

де позначено

. (3.31)

З формул (3.28)-(3.30) можна зробити висновок, що в електричному колі з індуктивним елементом ЕРС самоіндукції відстає від сили струму за фазою на кут , напруга випереджає силу струму за фазою на кут .

Розділивши праву і ліву частини виразу (3.31) на , одержимо закон Ома для діючих значень для електричного кола змінного струму з індуктивним елементом:

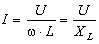, (3.32)

де позначено

, [Ом] (3.33)

індуктивний опір або реактивний опір індуктивного елемента.

Індуктивний опір – реактивний опір, зумовлений індуктивністю електричного кола; дорівнює добутку кутової частоти та індуктивності.

Фізично реактивний опір індуктивного елемента враховує вплив ЕРС самоіндукції на величину сили струму в колі. Зі зростанням частоти опір збільшується: при ω → ∞ XL → ∞. При ω → ∞ XL → ∞, тобто при постійному струмі індуктивний опір дорівнює нулю.

В електричному колі з індуктивним елементом закон Ома справедливий для діючих значень сили струму і напруги, для миттєвих значень сили струму та напруги закон Ома записати не можна (це справедливо для всіх кіл з реактивними елементами).

На рис. 3.16 приведено часову діаграму сили струму, напруги та ЕРС самоіндукції для електричного кола змінного струму з індуктивним елементом.

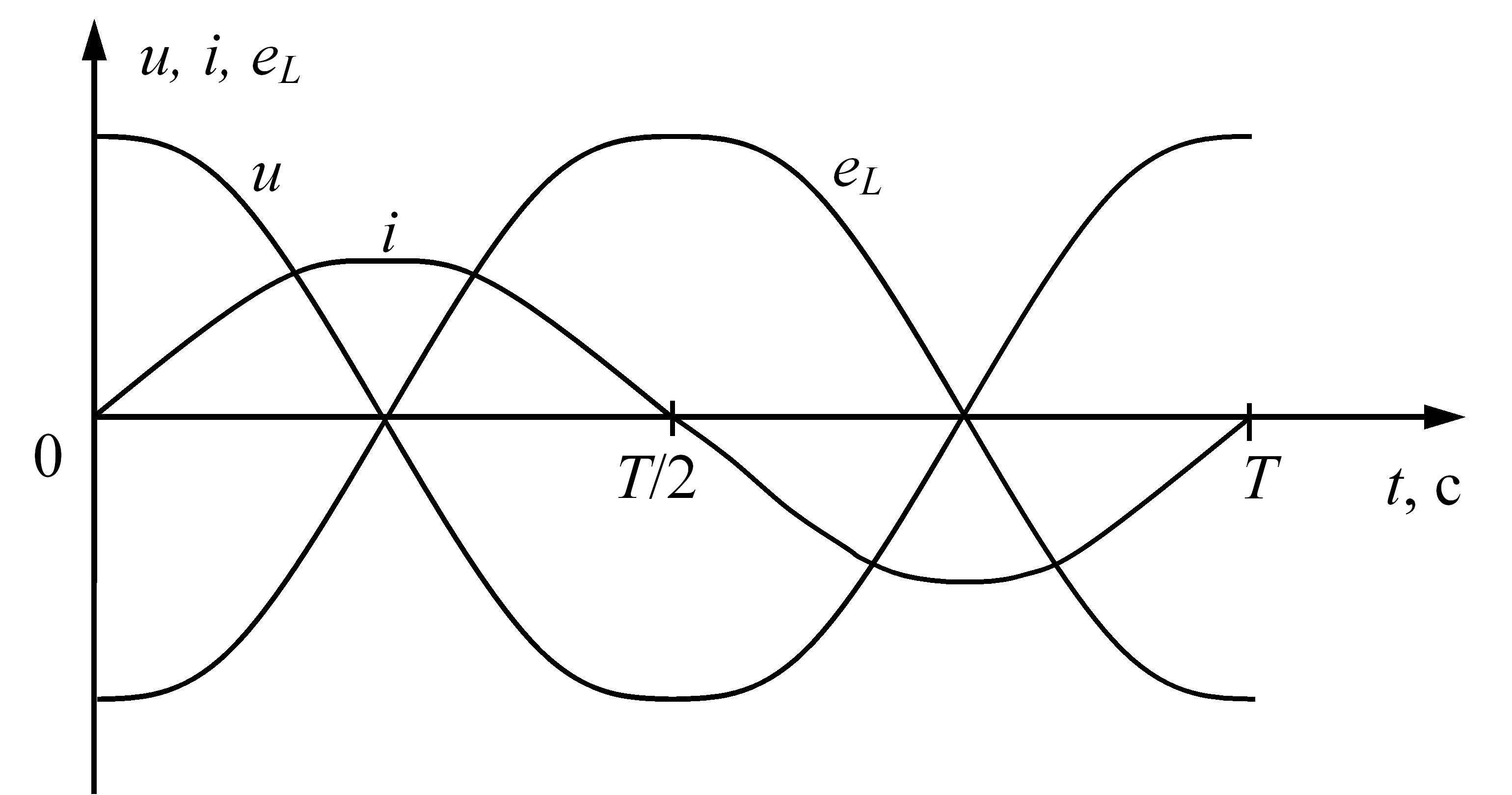
Рис. 3.16 – Часова діаграма сили струму, напруги та ЕРС самоіндукції для електричного кола змінного струму з індуктивним елементом

Векторну діаграму сили струму, напруги та ЕРС самоіндукції для електричного кола змінного струму з індуктивним елементом приведено на рис. 3.17.

Рис. 3.17 – Векторна діаграма сили струму, напруги та ЕРС самоіндукції для електричного кола змінного струму з індуктивним елементом

Визначимо потужність електрич-ного кола змінного струму з індуктивним елементом.

Миттєва потужність для аналізованого кола характеризує швидкість перетворення енергії джерела в енергію магнітного поля:

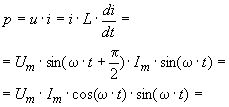
(3.34)

Видно, що миттєва потужність змінюється в часі з подвійною частотою ω. В електричному колі відбувається періодичний обмін енергією між генератором і магнітним полем кола без перетворення електричної енергії в теплову.

Часову діаграму миттєвої потужності для електричного кола змінного струму з індуктивним елементом приведено рис. 3.18.

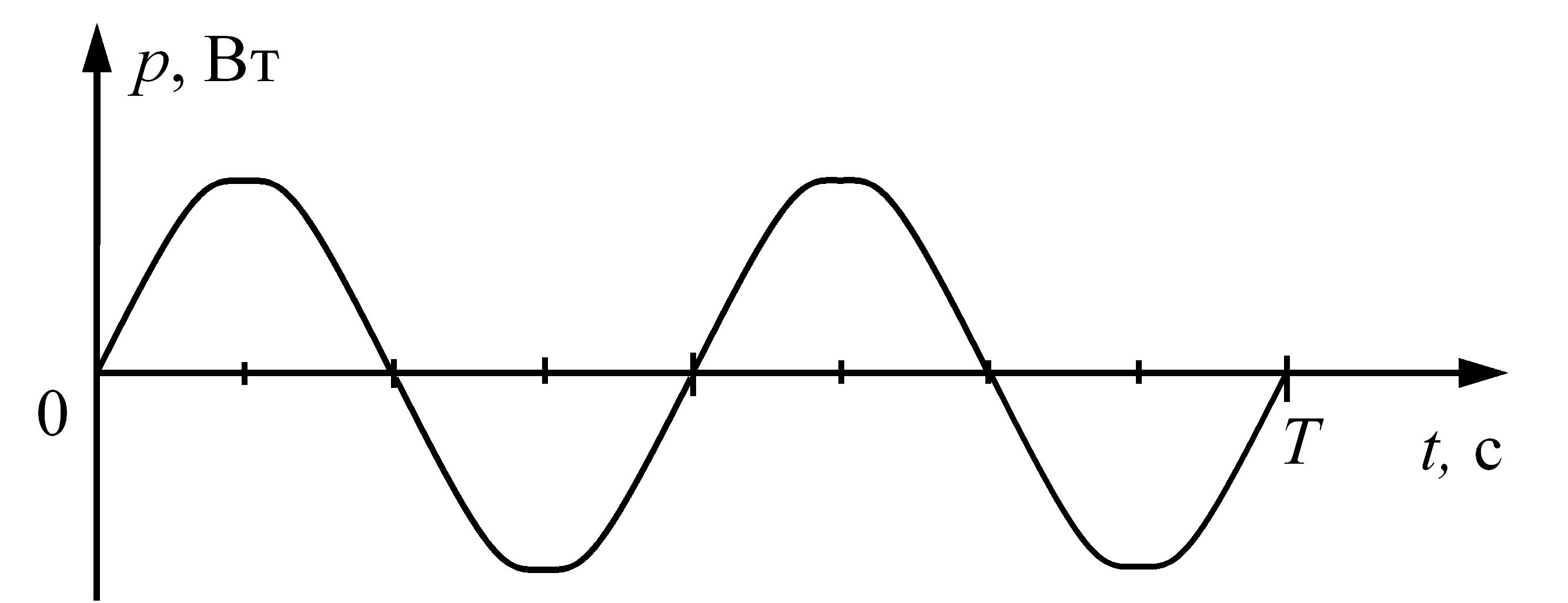
Рис. 3.18 – Часова діаграма миттєвої потужності для електричного кола змінного струму з індуктивним елементом

Середня за період активна потужність кола дорівнює нулю.

Реактивна потужність (позначається латинською літерою Q; одиниця виміру позначається [ВАр], називається "вольт-ампер-реактивний") – фізична величина, що дорівнює максимальному значенню миттєвої потужності кола з реактивним елементом. Для індуктивного елемента реактивна потужність визначається за формулою:

(3.35)

Електричне коло з ємнісним елементом. Розглянемо електричне коло змінного струму з ємнісним елементом (конденсатором) з ємністю величиною С (рис. 3.19), затискачі якого підключено до джерела синусоїдальної напруги u:

(3.36)

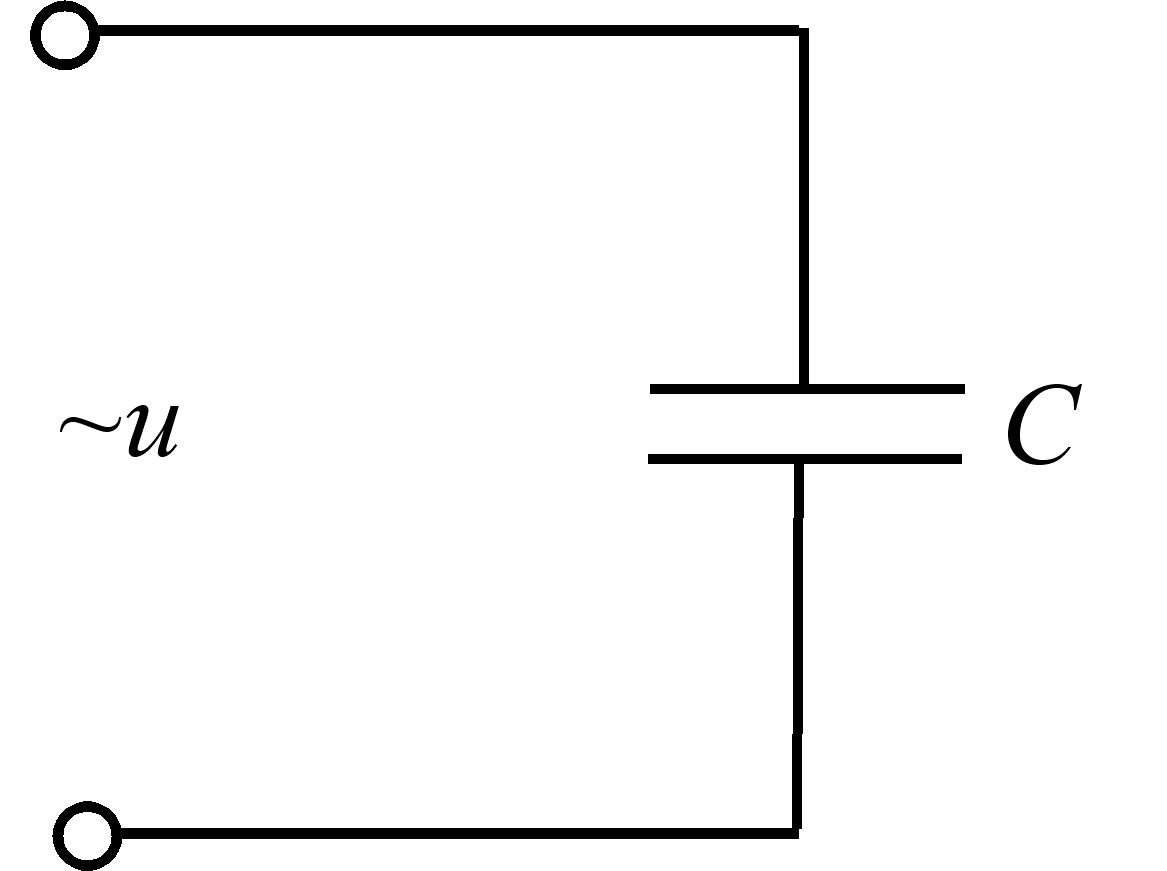
Рис. 3.19 – Коло змінного струму з ємнісним елементом

За визначенням сила струму – кількість електрики, що протікає через поперечний переріз провідника в одиницю часу. Для змінних величин:

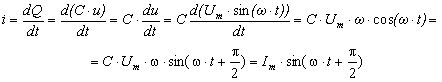(3.37)

де позначено

. (3.38)

З формул (3.36)-(3.37) можна зробити висновок, що в електричному колі напруга відстає від сили струму на кут .

Розділивши праву і ліву частини виразу (3.38) на , одержимо закон Ома для діючих значень для електричного кола змінного струму з ємнісним елементом:

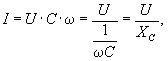(3.39)

де

(3.40)

ємнісний опір або реактивний опір ємнісного елемента.

Ємнісний опір – реактивний опір, обумовлений ємністю електричного кола; дорівнює величині, оберненій добутку кутової частоти та ємності.

Фізично реактивний опір ємнісного елемента являє собою реакцію цього елемента на його заряджання та розряджання. Зі збільшенням частоти ємнісний опір зменшується (при ω → ∞ XC→ 0), за зменшення частоти – відповідно збільшується (при ω → 0 XC→ ∞ ). Для постійного струму ємнісний елемент являє собою розрив кола. За змінної напруги ємнісний елемент періодично заряджається і розряджається, тому в електричному колі існує змінний струм.

На рис. 3.20 приведено часову діаграму сили струму та напруги для електричного кола змінного струму з ємнісним елементом.

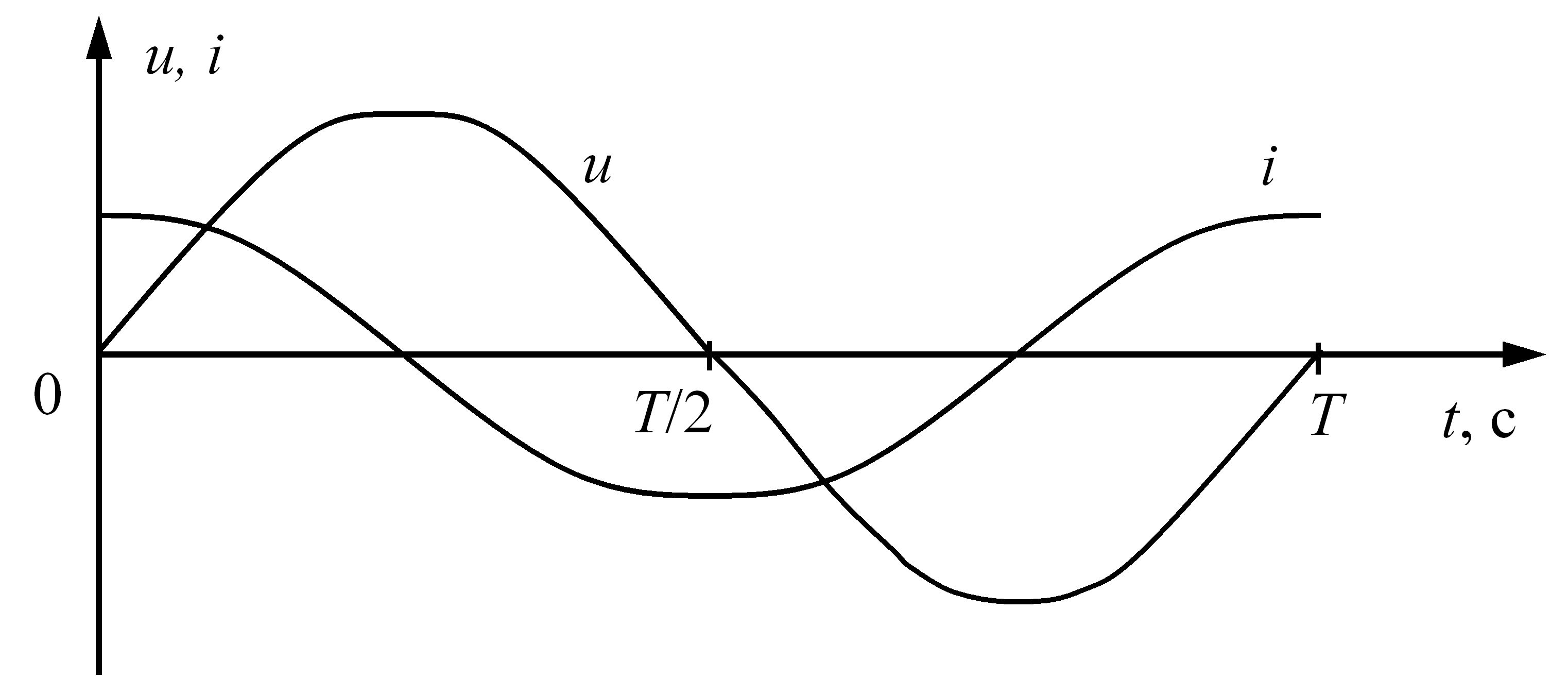
Рис. 3.20 – Часова діаграма сили струму та напруги для електричного кола змінного струму з ємнісним елементом

Векторну діаграму сили струму та напруги для електричного кола змінного струму з ємнісним елементом приведено на рис. 3.21.

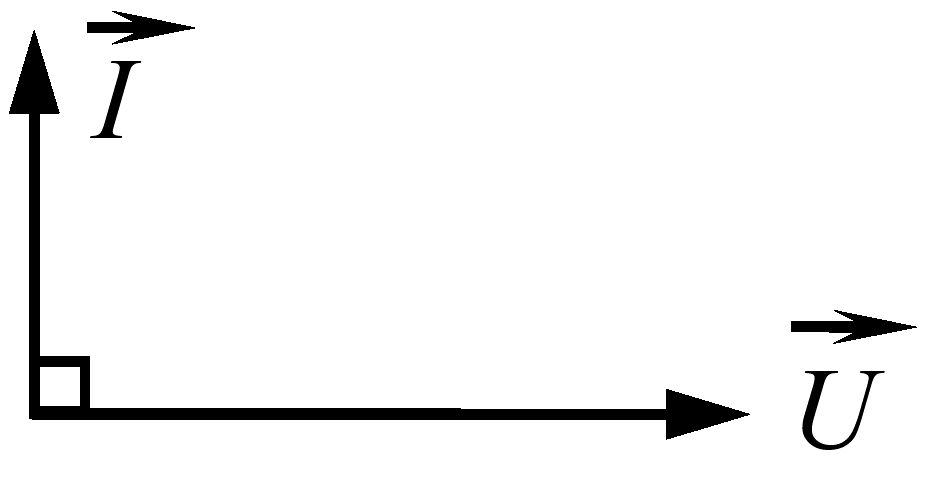
Рис. 3.21 – Векторна діаграма сили струму та напруги для електричного кола змінного струму з ємнісним елементом

Визначимо потужність електричного кола змінного струму з ємнісним елементом.

Миттєва потужність:

(3.41)

Миттєва потужність, як і в електричному колі з індуктивним елементом, змінюється в часі з подвійною частотою ω, але у протифазі. В електричному колі з ємнісним елементом відбувається періодичний обмін енергією між генератором і магнітним полем кола без перетворення електричної енергії в теплову.

Часову діаграму миттєвої потужності для електричного кола змінного струму з ємнісним елементом приведено рис. 3.22.

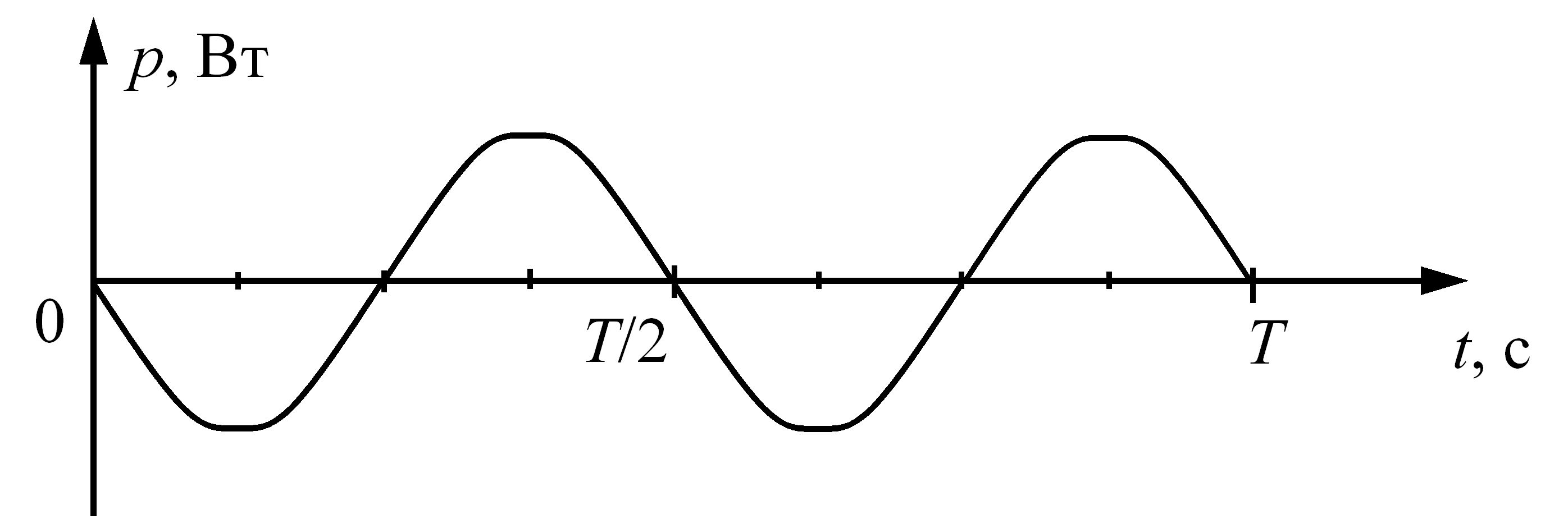
Рис. 3.22 – Часова діаграма миттєвої потужності для електричного кола змінного струму з ємнісним елементом

Середня за період потужність електричного кола дорівнює нулю.

Реактивна потужність електричного кола визначається за формулою:

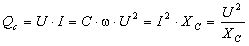. (3.42)

Послідовне з’єднання резистивного та індуктивного елементів. Електричні кола з послідовно з’єднаними елементами називаються нерозгалуженими.

Розглянемо електричне коло, зображене на рис. 3.23, затискачі якого підключено до джерела синусоїдальної напруги u.

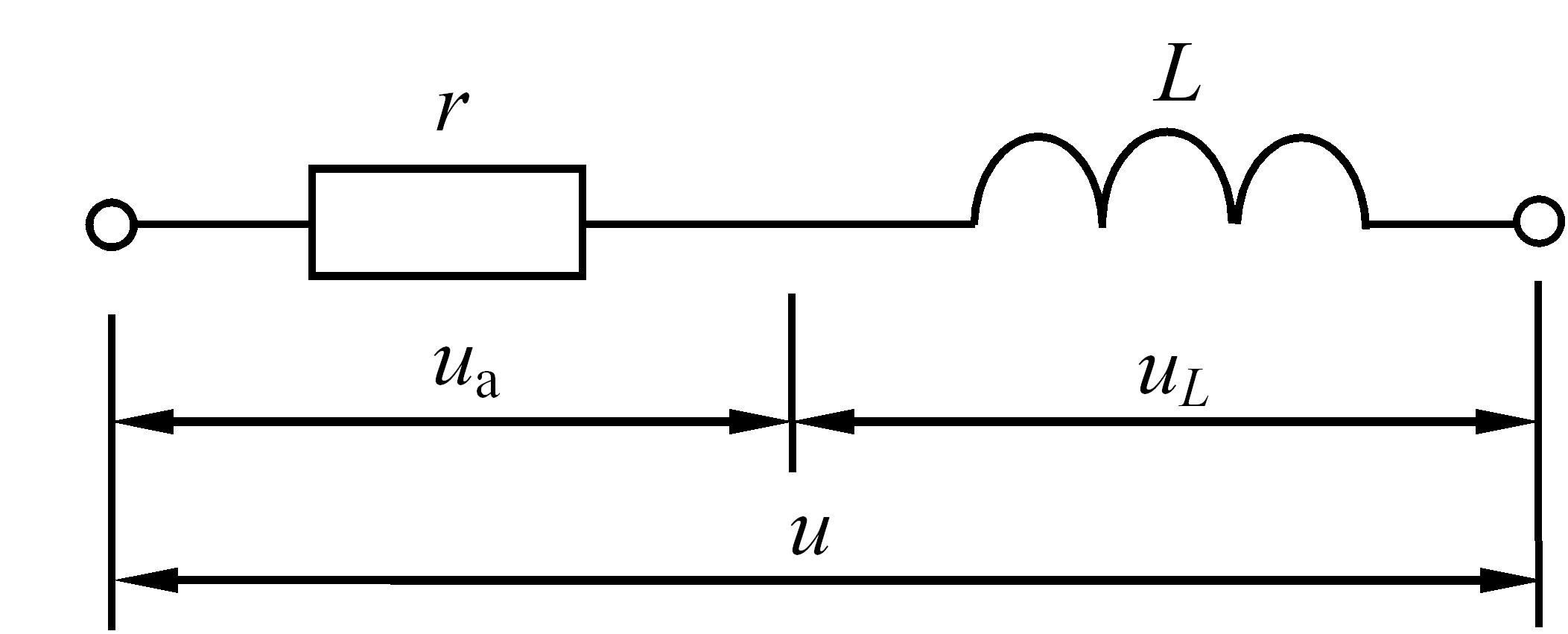
Рис. 3.23 – Електричне коло змінного струму з послідовно
з’єднаними резистивним та індуктивним елементами

Припустимо, що в колі існує електричний струм:

. (3.43)

На затискачах кола маємо миттєве значення напруги, яке складається з активної та індуктивної напруг:

. (3.44)

Активна складова напруги дорівнює:

. (3.45)

ЕРС індукції:

. (3.46)

Індуктивна складова напруги дорівнює:

(3.47)

Миттєві значення активної напруги та сили струму збігаються за фазою:

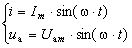. (3.48)

Індуктивна напруга випереджає силу струму за фазою на кут π/2:

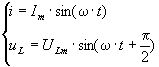. (3.49)

Миттєве значення напруги визначається за формулою:

. (3.50)

На рис. 3.24 приведено часову діаграму сили струму та напруги для електричного кола змінного струму з послідовно з’єднаними резистивним та індуктивним елементами.

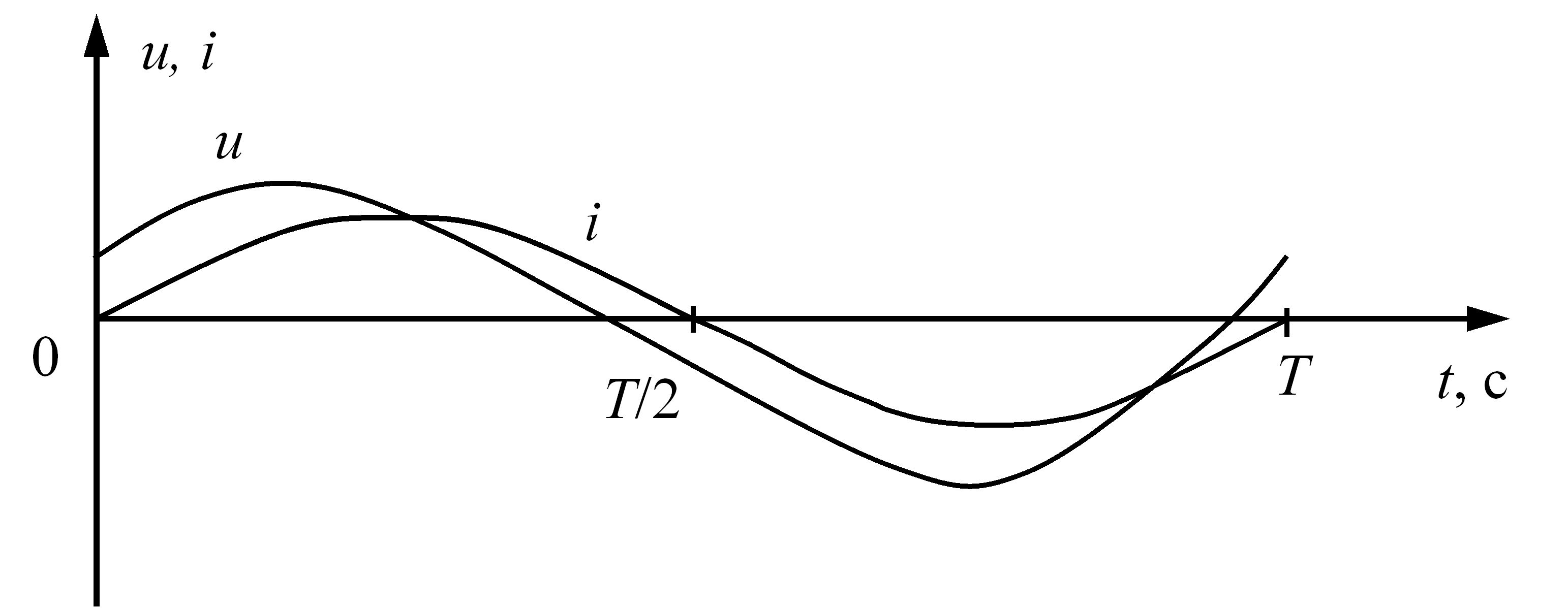
Рис. 3.24 – Часова діаграма сили струму та напруги для електричного кола змінного струму з послідовно з’єднаними резистивним та
індуктивним елементами

Векторну діаграму сили струму та напруг (для діючих значень) для електричного кола змінного струму з послідовно з’єднаними резистивним та індуктивним елементами приведено на рис. 3.25.

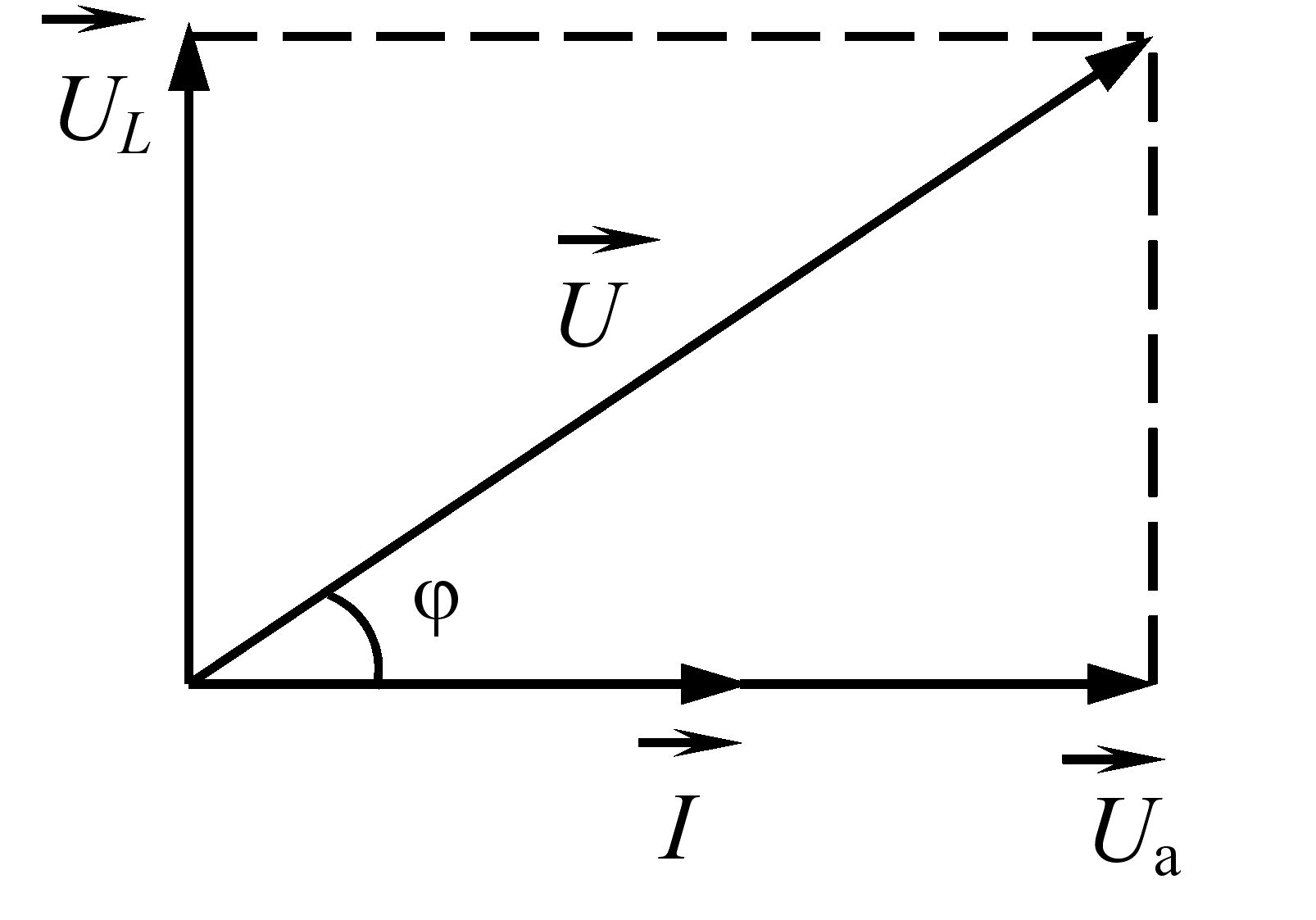
Рис. 3.25 – Векторна діаграма сили струму та напруг для електричного кола змінного струму з послідовно з’єднаними резистивним та індуктивним елементами

Напруги на векторній діаграмі створюють трикутник напруг. З трикутника напруг видно, що діючі значення напруги U, Ua , UL пов’язані між собою як сторони прямокутного трикутника. За теоремою Піфагора:

. (3.51)

Кут зсуву фаз між векторами сили струму і напруги визначається з векторної діаграми на рис. 3.25:

(3.52)

Після перетворення формули (3.51)

отримуємо закон Ома для діючих значень для електричного кола змінного струму з послідовно з’єднаними резистивним та індуктивним елементами:

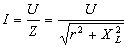. (3.53)

Величина

(3.54)

називається повним опором кола, вимірюється в [Ом].

Графічно опори r, XL , Z зображуються у вигляді прямокутного трикутника, який називається "трикутник опорів". Трикутник опорів створюється шляхом зменшення в І раз сторін трикутника напруг. Трикутник опорів для електричного кола змінного струму з послідовно з’єднаними резистивним та індуктивним елементами приведений на рис. 3.26,а.

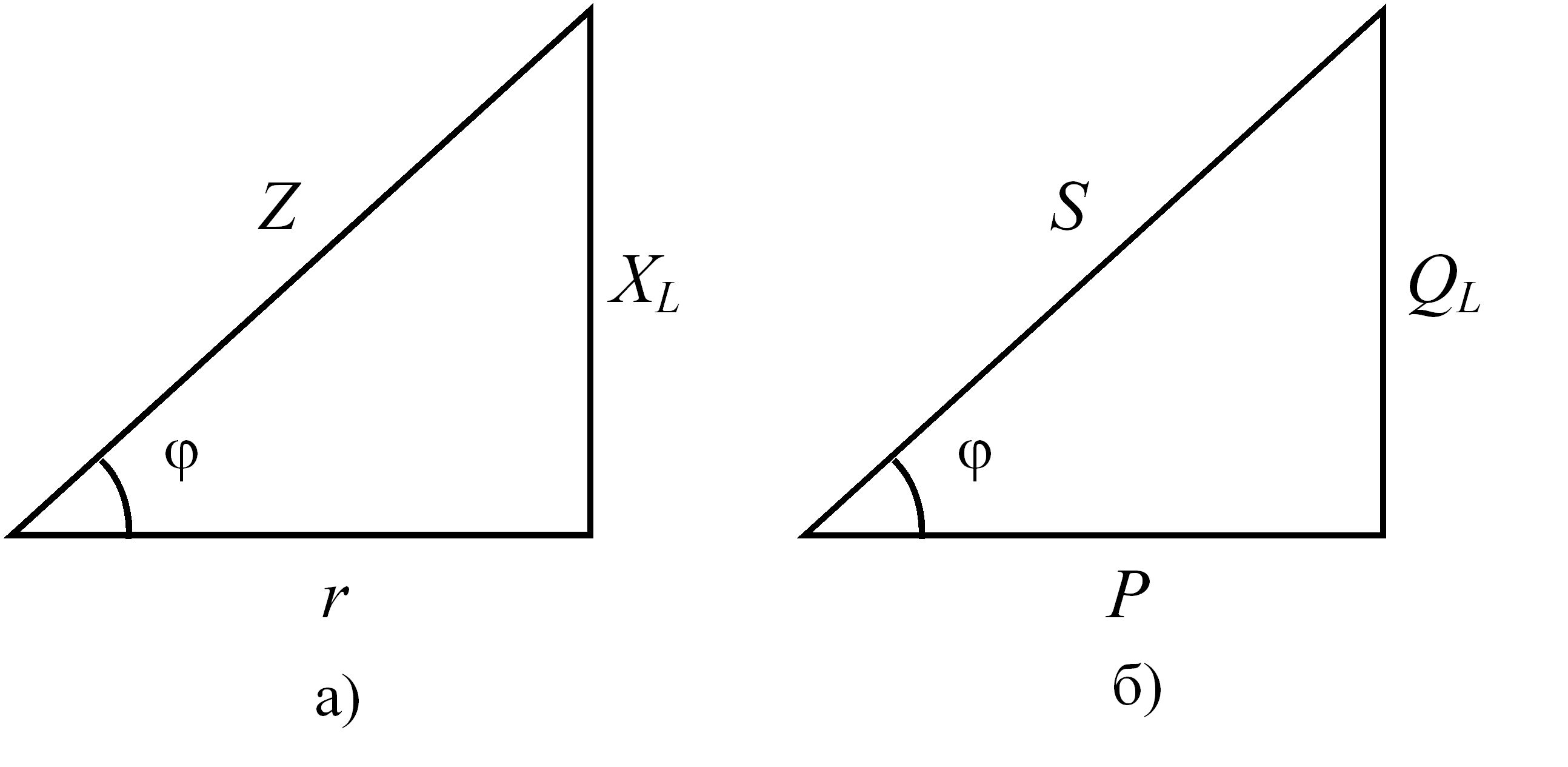
Рис. 3.26 – Трикутник опорів (а) та трикутник потужностей (б) для електричного кола змінного струму з послідовно з’єднаними резистивним та індуктивним елементами

Раніше було введено поняття миттєвої p, активної P та реактивної QL потужностей. Для електричних кіл, що містять активні та реактивні елементи, вводиться поняття повної потужності.

Повна потужність (позначається латинською літерою S; одиниця виміру позначається [ВА], називається "вольт-ампер") – фізична величина, що дорівнює добутку діючих значень напруги та струму. Математично повна потужність визначається за формулою:

. (3.55)

Потужності S, P, QL пов’язані між собою як сторони прямокутного трикутника, який називається "трикутник потужностей". Трикутник потужностей створюється шляхом збільшення в І раз сторін трикутника напруг (зображений на рис. 3.26,б). З трикутника очевидно:

. (3.56)

Послідовне з’єднання резистивного та ємнісного елементів. Розглянемо електричне коло, зображене на рис. 3.27, затискачі якого підключено до джерела синусоїдальної напруги u.

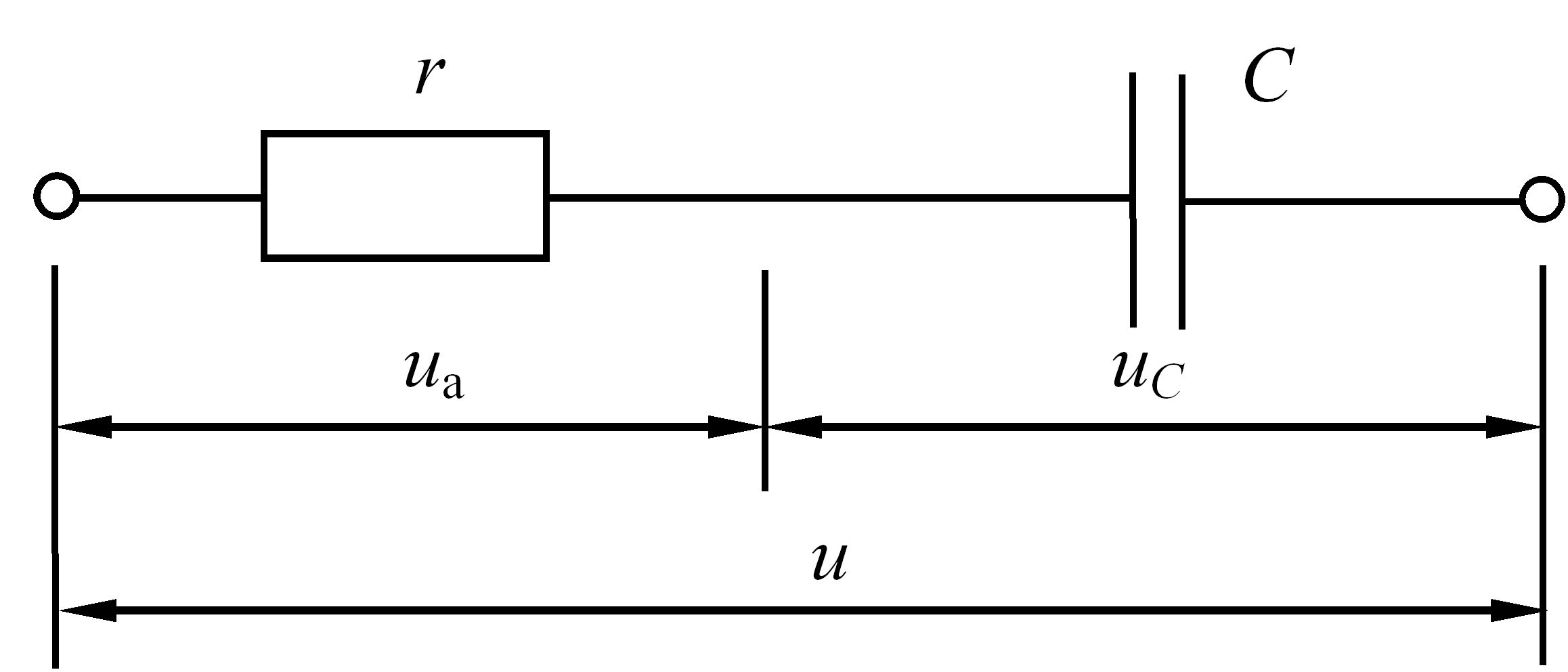
Рис. 3.27 – Електричне коло змінного струму з послідовно з’єднаними резистивним та ємнісним елементами

Припустимо, що в колі існує електричний струм:

На затискачах кола маємо напругу:

. (3.57)

Активна складова напруги дорівнює:

. (3.58)

На резистивному елементі напруга та сила струму збігаються за фазою.

Визначимо ємнісну складову напруги. Для ємнісного елемента можна записати:

На ємнісному елементі напруга відстає від сили струму на кут π/2:

(3.59)

Миттєве значення напруги:

. (3.60)

Векторну діаграму сили струму та напруг для електричного кола змінного струму з послідовно з’єднаними резистивним та ємнісним елементами приведено на рис. 3.28.

Напруги на векторній діаграмі створюють трикутник напруг. Діючі значення напруги U, Ua ,UC пов’язані між собою як сторони прямокутного трикутника. За теоремою Піфагора:

. (3.61)

Кут зсуву фаз між векторами сили струму і напруги визначається з векторної діаграми (рис. 3.28):

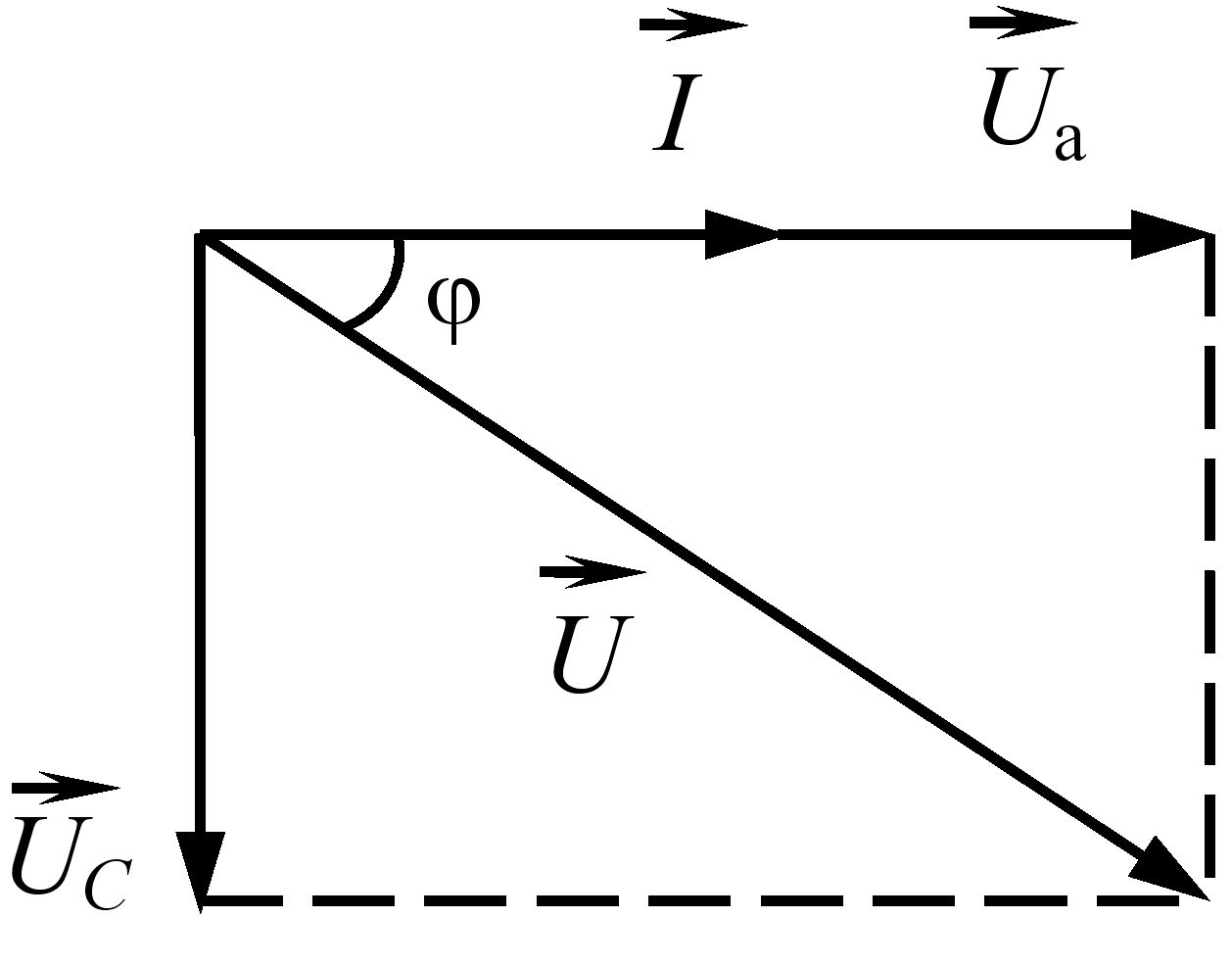
Рис. 3.28 – Векторна діаграма сили струму та напруг для електричного кола змінного струму з послідовно з’єднаними резистивним та ємнісним елементами

(3.62)

Після перетворення формули (3.61)

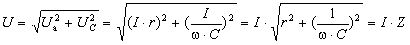
отримуємо закон Ома для діючих значень для електричного кола змінного струму з послідовно з’єднаними резистивним та ємнісним елементами:

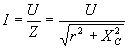, (3.63)

де – повний опір кола.

Трикутник опорів для електричного кола змінного струму з послідовно з’єднаними резистивним та ємнісним елементами приведений на рис. 3.29,а, трикутник потужностей – на рис. 3.29,б.

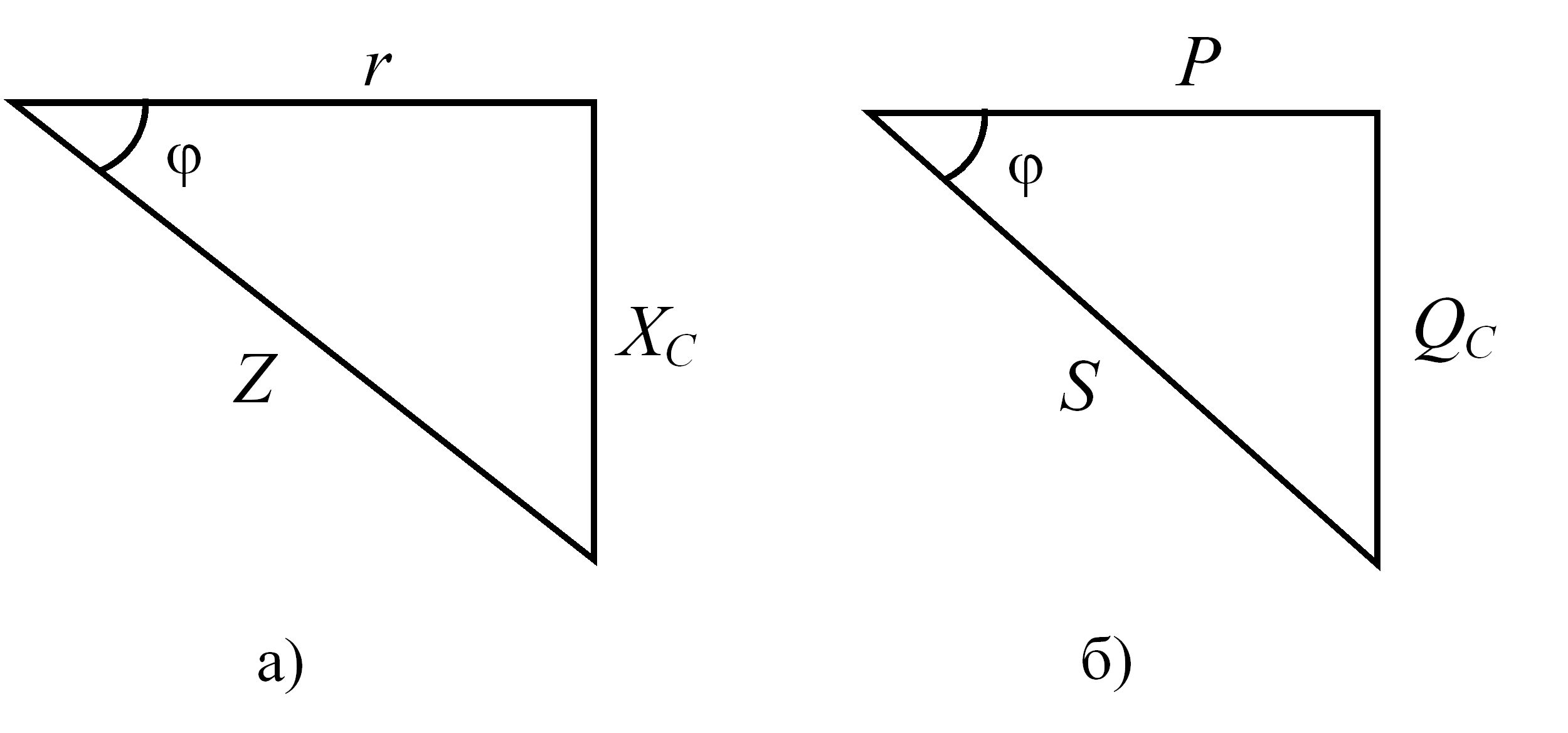
Рис. 3.29 – Трикутник опорів (а) та трикутник потужностей (б) для електричного кола змінного струму з послідовно з’єднаними резистивним та ємнісним елементами

Послідовне з’єднання резистивного, індуктивного та ємнісного елементів. Розглянемо електричне коло, зображене на рис. 3.30.

Припустимо, що в колі існує електричний струм:

На затискачах кола маємо миттєве значення напруги:

(3.64)

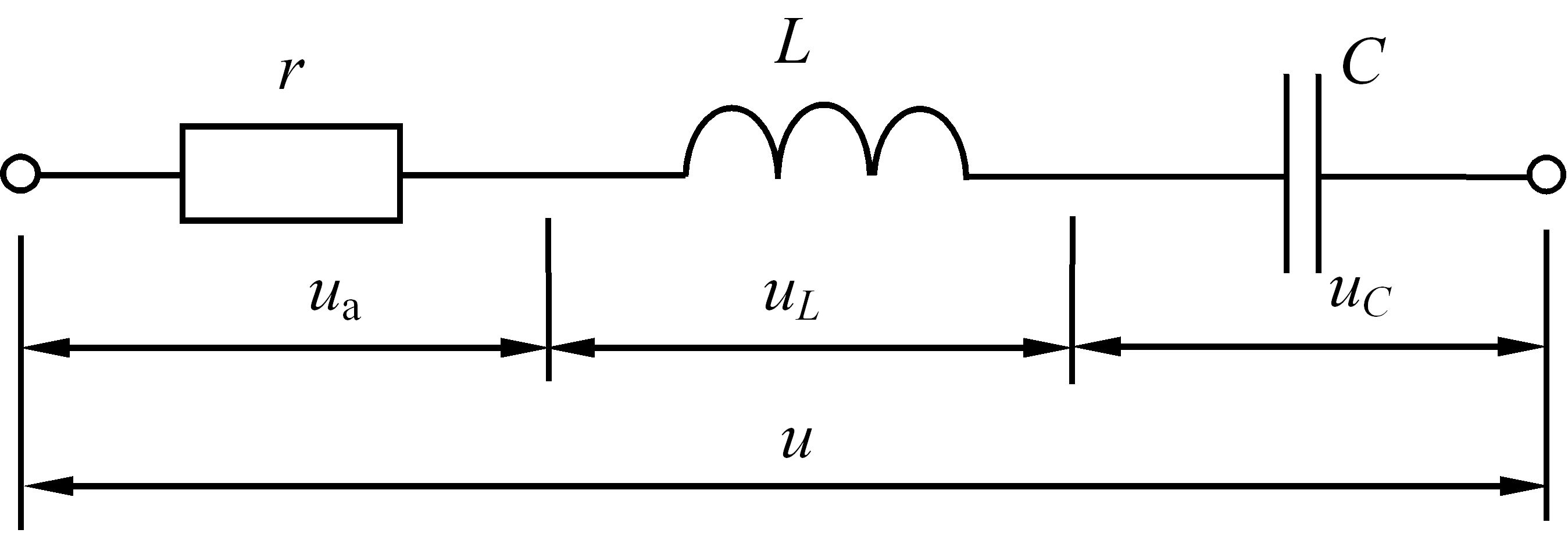
Рис. 3.30 – Електричне коло змінного струму з послідовно з’єднаними резистивним, індуктивним та ємнісним елементами

Напруги на індуктивному та ємнісному елементах зсунуті одна відносно одної за фазою на кут π. Їх алгебраїчна сума називається реактивною напругою та позначається up:

(3.65)

Таким чином, напруга на затискачах кола:

(3.66)

Векторна діаграма сили струму та напруг (для діючих значень) для електричного кола змінного струму з послідовно з’єднаними резистивним, індуктивним та ємнісним елементами при UL>UC приведена на рис. 3.31.

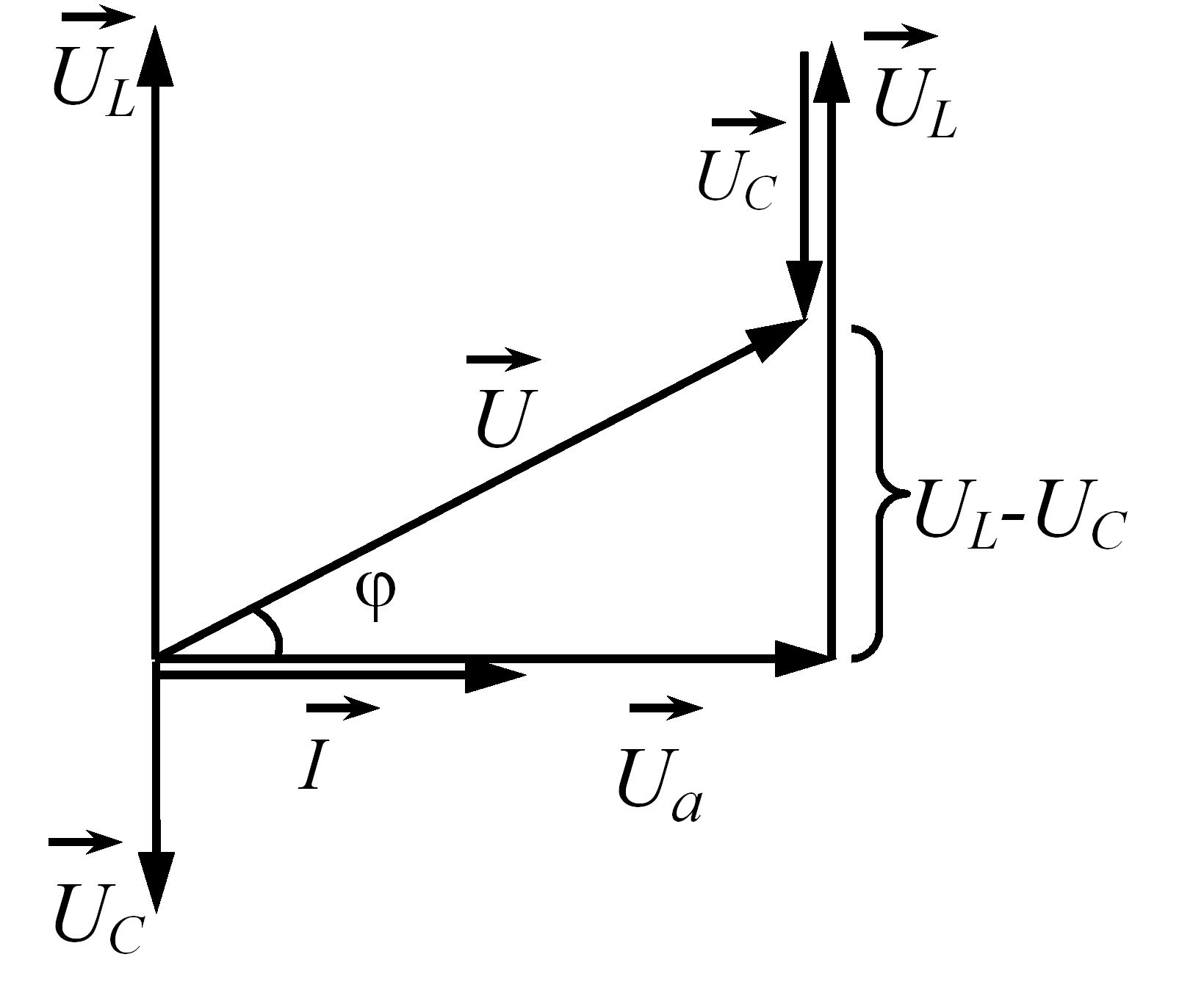
Рис. 3.31 – Векторна діаграма сили струму та напруг для електричного кола змінного струму з послідовно з’єднаними резистивним, індуктивним та ємнісним елементами при

UL>UC

З векторної діаграми очевидно, що діючі значення напруги U, Ua , UL , UC пов’язані між собою співвідношенням:

. (3.67)

Кут зсуву фаз між векторами сили струму і напруги визначається зі співвідношення:

(3.68)

Після перетворення формули (3.67)

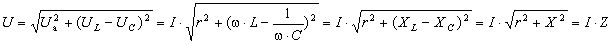
отримуємо закон Ома для діючих значень для електричного кола змінного струму з послідовно з’єднаними резистивним, індуктивним та ємнісним елементами:

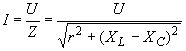, (3. 69)

де – повний опір кола; Х – реактивний опір кола – алгебраїчна величина (може бути як позитивним, так і негативним).

Резонанс напруг. За рівності індуктивного й ємнісного опорів (XL=XC) в електричному колі змінного струму з послідовно з’єднаними індуктивним та ємнісним елементами кут між векторами сили струму і загальної напруги дорівнює нулю, тобто сила струму і напруга збігаються за фазою. У такому режимі в електричному колі має місце резонанс напруг. Таким чином, при резонансі напруг реактивний опір кола дорівнює нулю.

Умова резонансу напруг математично записується наступним чином:

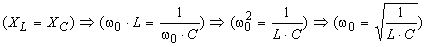, (3.70)

де ω0 – кутова резонансна частота.

Векторна діаграма сили струму та напруг для електричного кола змінного струму з послідовно з’єднаними резистивним, індуктивним та ємнісним елементами при резонансі напруг подана на рис. 3.32 (довжини векторів індуктивної та ємнісної напруг є однаковими).

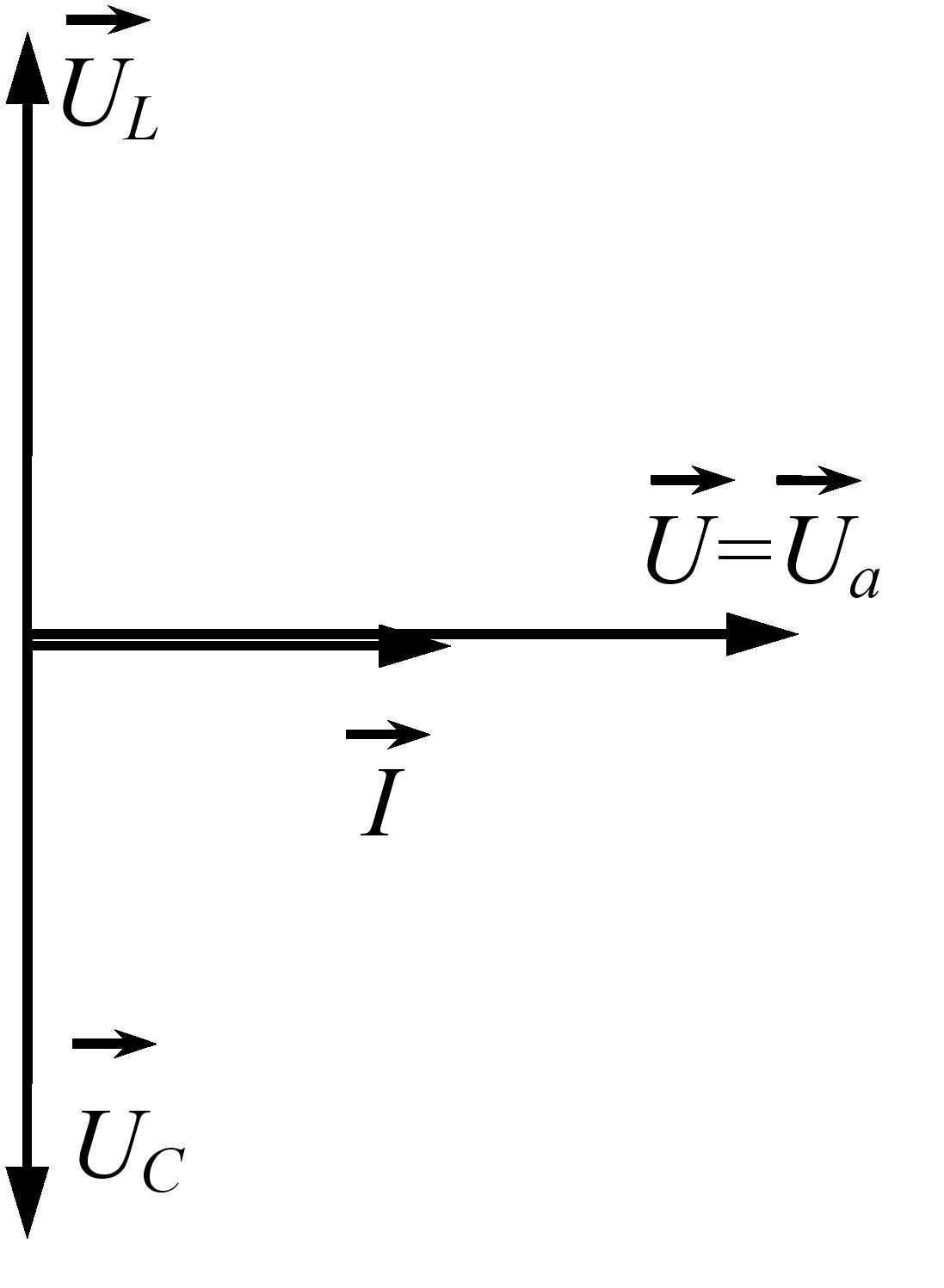
Рис. 3.32 – Векторна діаграма сили струму та напруг для електричного кола змінного струму з послідовно з’єднаними резистивним, індуктивним та ємнісним елементами при резонансі напруг

При резонансі напруг коло поводиться так, начебто воно містить тільки резистивний елемент з активним опором. При цьому повний опір кола дорівнює активному (Z=r), а сила струму в колі буде максимальною.

Пожежна небезпека резонансу напруг полягає у тому, що напруга на індуктивності UL та напруга на ємності UC при великих опорах XL та XC і малому опорі r можуть значно перевищувати напругу на затискачах кола U. Значне збільшення напруги на ділянках кола може призвести до пробою ізоляції проводів котушок, пробою діелектрика конденсаторів, нагріву провідників, тобто може виникнути пожежа.

Паралельне з’єднання реальної котушки індуктивності та ємнісного елемента. Електричні кола з паралельно з’єднаними елементами називаються розгалуженими.

Розглянемо електричне коло, що складається з двох паралельно з’єднаних віток, одна з яких містить реальну котушку індуктивності, а друга – ємнісний елемент (рис. 3.33).

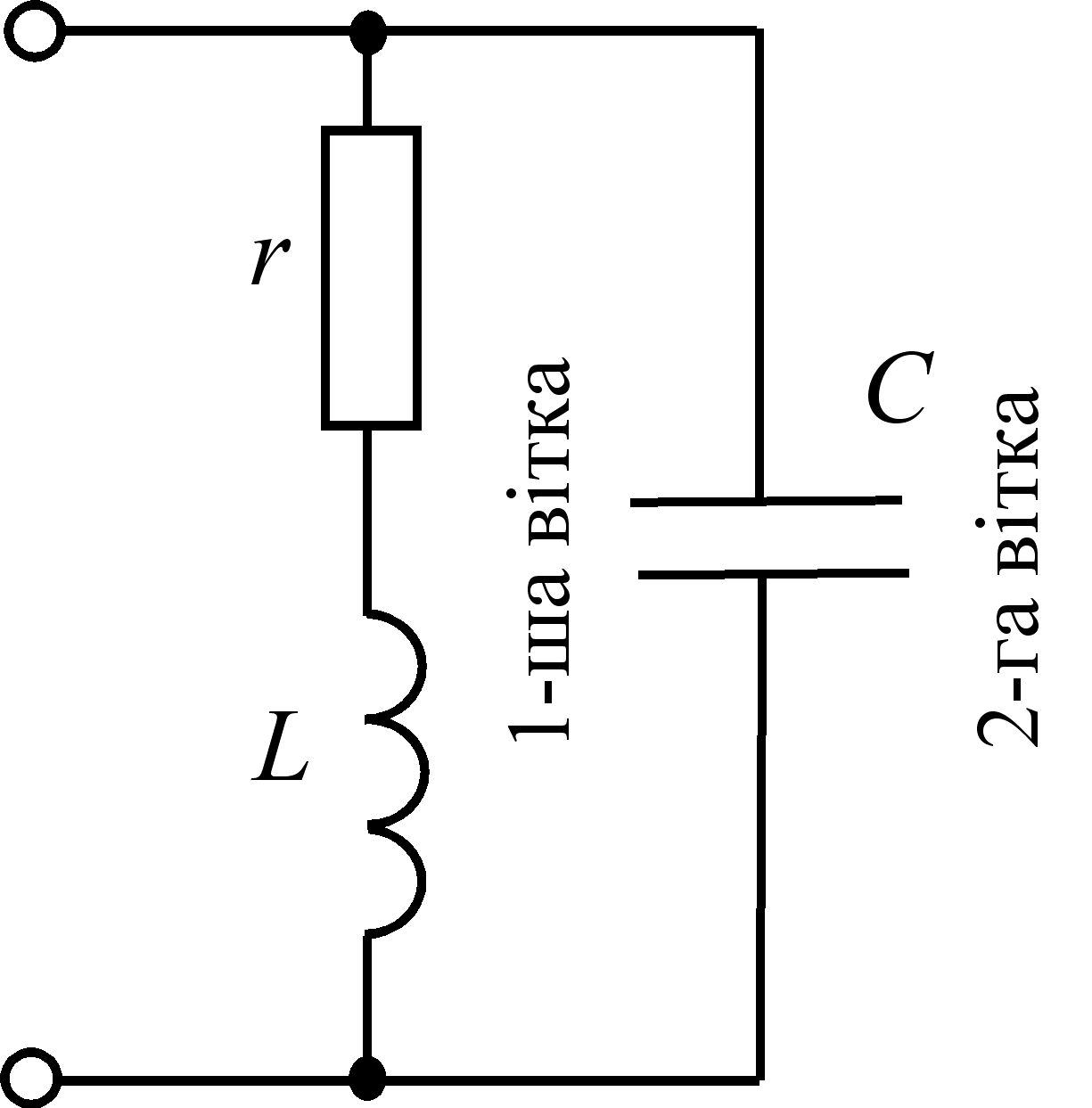
Рис. 3.33 – Електричне коло змінного струму з паралельно з’єднаними реальною котушкою індуктивності та ємнісним елементом

Реальна котушка індуктивності має еквівалентну схему у вигляді послідовно з’єднаних резистивного елемента з активним опором r та індуктивного елемента (ідеальної котушки індуктивності) з індуктивністю L.

Для визначення величин струмів у вітках звичайно використовується метод провідностей. Для застосування цього методу сили струмів у вітках і в нерозгалуженій частині кола слід представити у виді двох складових – активної (Ia) та реактивної (Ip).

Сили струму в кожній вітці, їх реактивні та активні складові пов’язані між собою діаграмою сил струмів та напруги. Наприклад, за умови, що індуктивний струм є меншим за ємнісний, діаграма сил струмів і напруги має вигляд, зображений на рис. 3.34,а (індекси при літерах позначають номер вітки).

Рис. 3.34 – Векторна діаграма сил струмів і напруги (а) та багатокутник провідностей (б) для електричного кола змінного струму з паралельно з’єднаними реальною котушкою індуктивності та ємнісним елементом

Повні опори відповідно першої та другої віток:

, .

Кут зсуву фаз між силою струму та напругою для першої вітки:

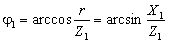Оскільки у другу вітку включений тільки ємнісний елемент з опором X2, кут зсуву фаз між силою струму та напругою для другої вітки дорівнює:

Сили струмів у вітках визначаються за законом Ома:

, .

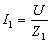Для визначення сили струму в нерозгалуженій частині кола необхідно знайти активні й реактивні складові сил струмів.

Активна складова сили струму першої вітки: .

Реактивна складова сили струму першої вітки: Ip1 = I1·sin φ1 .

Активна складова сили струму другої вітки: Ia2 = 0.

Реактивна складова сили струму другої вітки: Ip2 = I2.

Силу струму у нерозгалуженій частині кола визначаємо за формулою:

Кут зсуву фаз між силою струму та напругою для всього кола:

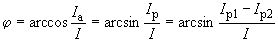Багатокутник провідностей одержується з векторної діаграми сил струмів зменшенням сторін у U раз (рис. 3.34,б).

На рис. 3.34,б застосовуються позначення:

Y – повна провідність усього кола (),

g – активна провідність усього кола,

B – реактивна провідність усього кола,

– повна провідність першої вітки (),

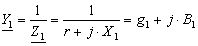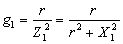– активна провідність першої вітки (),

– реактивна провідність першої вітки (),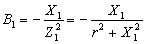

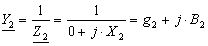Y2 – повна провідність другої вітки (),

– реактивна провідність другої вітки (),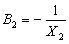

активна провідність другої вітки дорівнює нулю (g2= 0).

Резонанс струмів. За рівності індуктивної й ємнісної провідностей в електричному колі змінного струму з паралельно з’єднаними реальною котушкою індуктивності та ємнісним елементом кут між вектором сили струму у нерозгалуженій частині кола і вектором загальної напруги дорівнює нулю, тобто напруга і сила струму збігаються за фазою. У такому режимі в електричному колі має місце резонанс струмів. Таким чином, при резонансі струмів сумарна реактивна провідність кола дорівнює нулю.

Умова резонансу струмів для кола, зображеного на рис. 3.33, математично записується наступним чином:

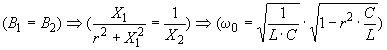, (3.71)

де ω0 – кутова резонансна частота.

За умов малості величини r математична умова резонансу струмів (3.71) співпаде з математичною умовою резонансу напруг (3.70).

Векторна діаграма сил струмів та напруги для електричного кола змінного струму з паралельно з’єднаними реальною котушкою індуктивності та ємнісним елементом при резонансі струмів приведена на рис. 3.35 (довжина векторів та є однаковою).

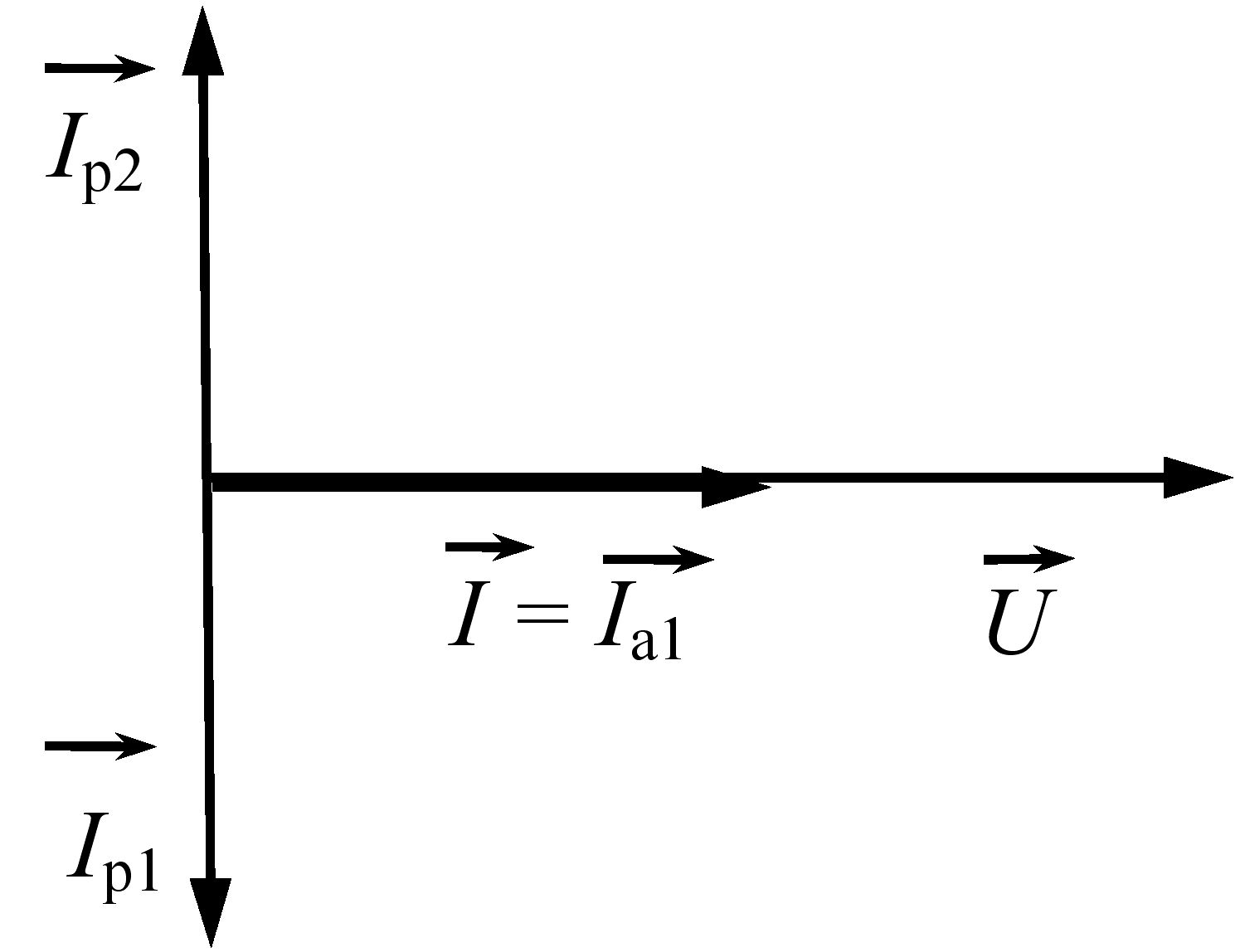
Рис. 3.35 – Векторна діаграма сил струмів та напруги для електричного кола змінного струму з паралельно з’єднаними реальною котушкою індуктивності та ємнісним елементом при резонансі струмів

При резонансі струмів в електричному колі між джерелом ЕРС та споживачем існує тільки активний струм, величина якого є мінімальною. Таким чином, включення ємнісного елемента (конденсатора) визначеної ємності паралельно приймачу, який має активно-індуктивний опір (наприклад, обмотка електродвигуна), зменшує загальний струм у колі. Тому при резонансі струмів пожежна небезпека зменшується.

Резонанс струмів може виникати в розгалуженому електричному колі, яке містить декілька віток із резистивними, індуктивними та ємнісними елементами, за умови, що сумарна реактивна провідність кола дорівнює нулю.

Резонанс напруг та резонанс струмів поєднуються загальним поняттям "резонанс в електричному колі".

Резонанс в електричному колі – фізичне явище в електричному колі, яке містить індуктивні та ємнісні елементи, при якому різниця фаз напруги та струму на вході кола дорівнює нулю.