3.12. З’єднання споживачів трифазного струму "трикутником"

Трифазні споживачі електроенергії з’єднуються за схемою "трикутник" у тих випадках, коли номінальна напруга фаз приймача електроенергії дорівнює лінійній напрузі тієї системи, що живить даний споживач трифазної мережі. "Трикутником" частіше усього включаються обмотки статорів двигунів змінного струму. Для живлення споживача, підключеного "трикутником", застосовується трипровідна трифазна мережа.

Схема з’єднання споживачів трифазного струму "трикутником" приведена на рис. 3.51. 

Лінійна напруга в мережі дорівнює фазній напрузі:  

.                                                      (3.89)

З’ясуємо співвідношення між силами лінійних і фазних струмів. Розглянемо окремо випадки симетричного та несиметричного навантаження.

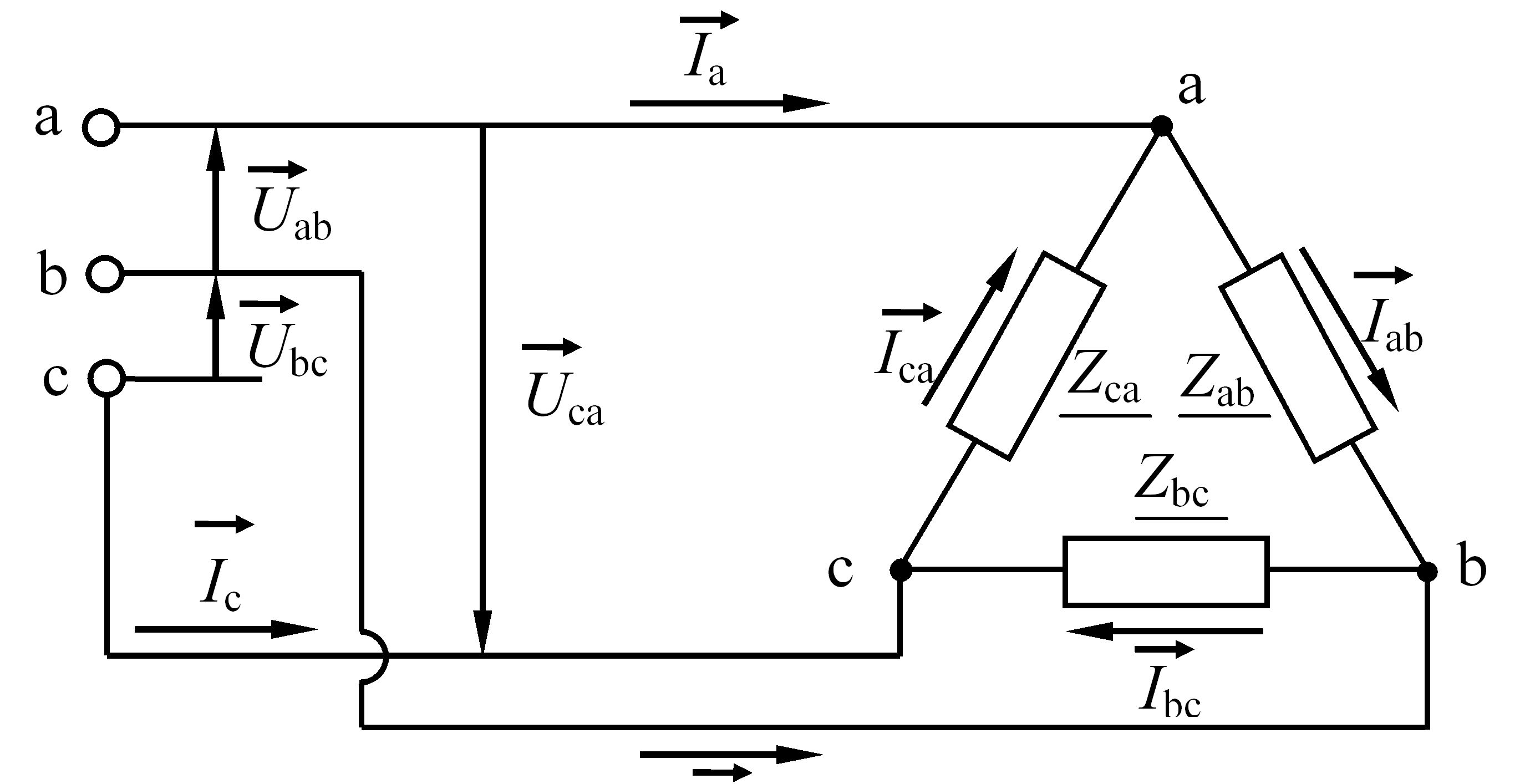
Рис. 3.51 – Схема з’єднання споживачів трифазного струму "трикутником"

Симетричне навантаження. Навантаження буде симетричним у випадку, коли в кожну фазу включено навантаження з однаковими повними опорами:

,                                                 (3.90)

тобто ===,φab = φbc = φca = φ, .

За позитивний напрямок лінійних струмів приймаємо напрямок від генератора до приймача, а позитивні напрямки фазних струмів – від a до b, від b до c та від c до a, як це показано стрілками на схемі (рис. 3.51). За першим законом Кірхгофа для вузлів схеми a, b, та c маємо:

,            ,                                          (3.91)

звідкіля

,         ,       .                       (3.92)

З цих векторних співвідношень випливає, що кожний з лінійних струмів є геометричною різницею відповідних фазних струмів.

Для аналізу векторних співвідношень (3.92) необхідно побудувати векторну діаграму. На рис. 3.52 побудовано векторну діаграму сил струмів і напруг для випадку симетричного активного навантаження.

При симетричному навантаженні фаз величини фазних струмів будуть рівні між собою за абсолютними значеннями:

 .                                                     (3.93)

Звідси й величини лінійних струмів також будуть рівні між собою за абсолютним значеннями:

.                                                       (3.94)

Співвідношення між величинами лінійних і фазних струмів знаходимо з векторної діаграми (рис. 3.52):   

.

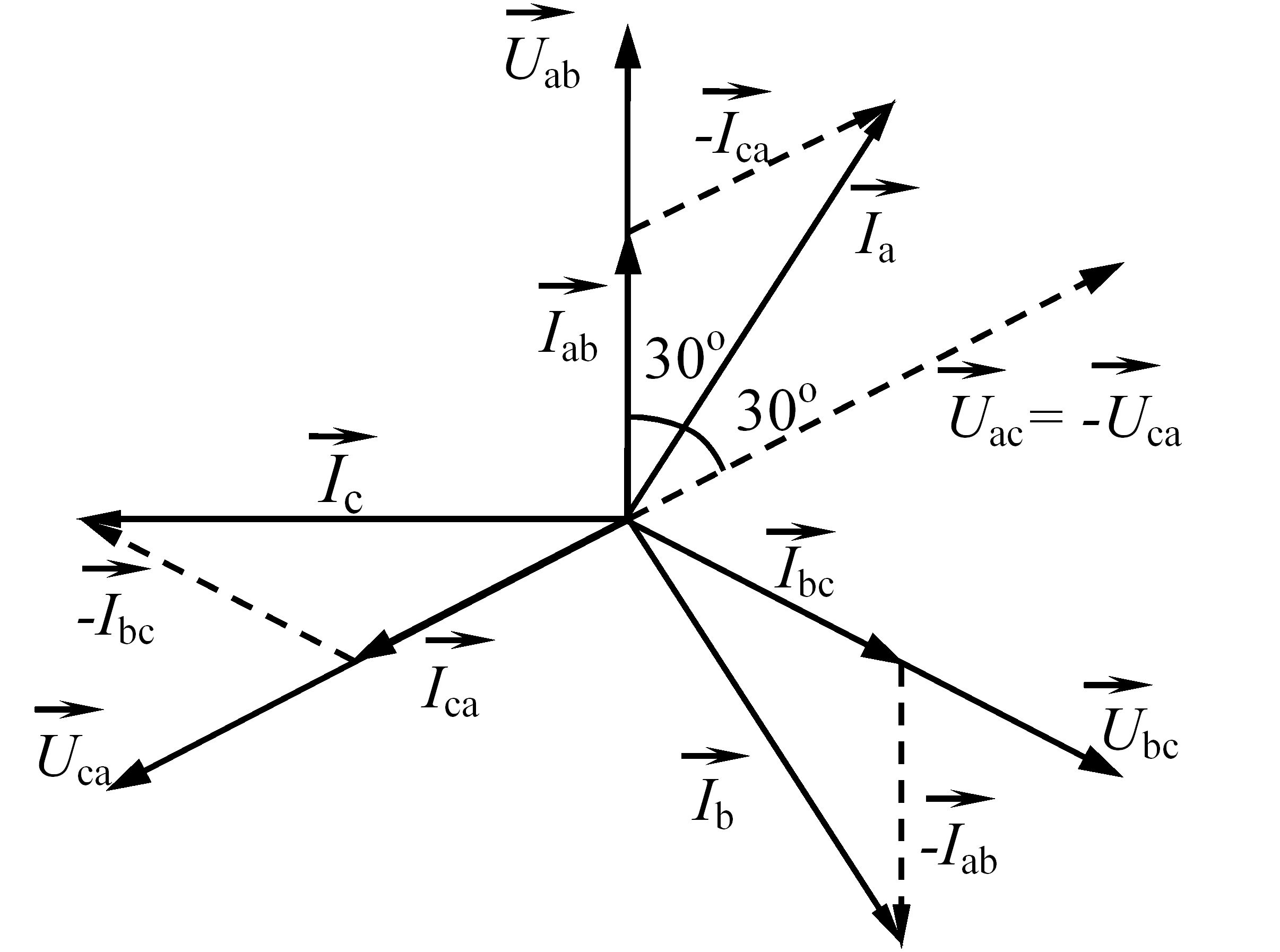
Рис. 3.52 – Векторна діаграма сил струмів і напруг для трифазного симетричного активного навантаження при з’єднанні споживачів трифазного струму "трикутником"

Враховуючи, що 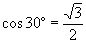, одержимо кінцеве співвідношення:

.                                                 (3.95)

Це співвідношення справедливе тільки для випадку симетричного навантаження. 

Якщо навантаження є змішаним, то φ ≠ 0. На рис. 3.53 для прикладу побудовано векторну діаграму сил струмів і напруг для випадку симетричного активно-індуктивного навантаження (cosφ < 1).

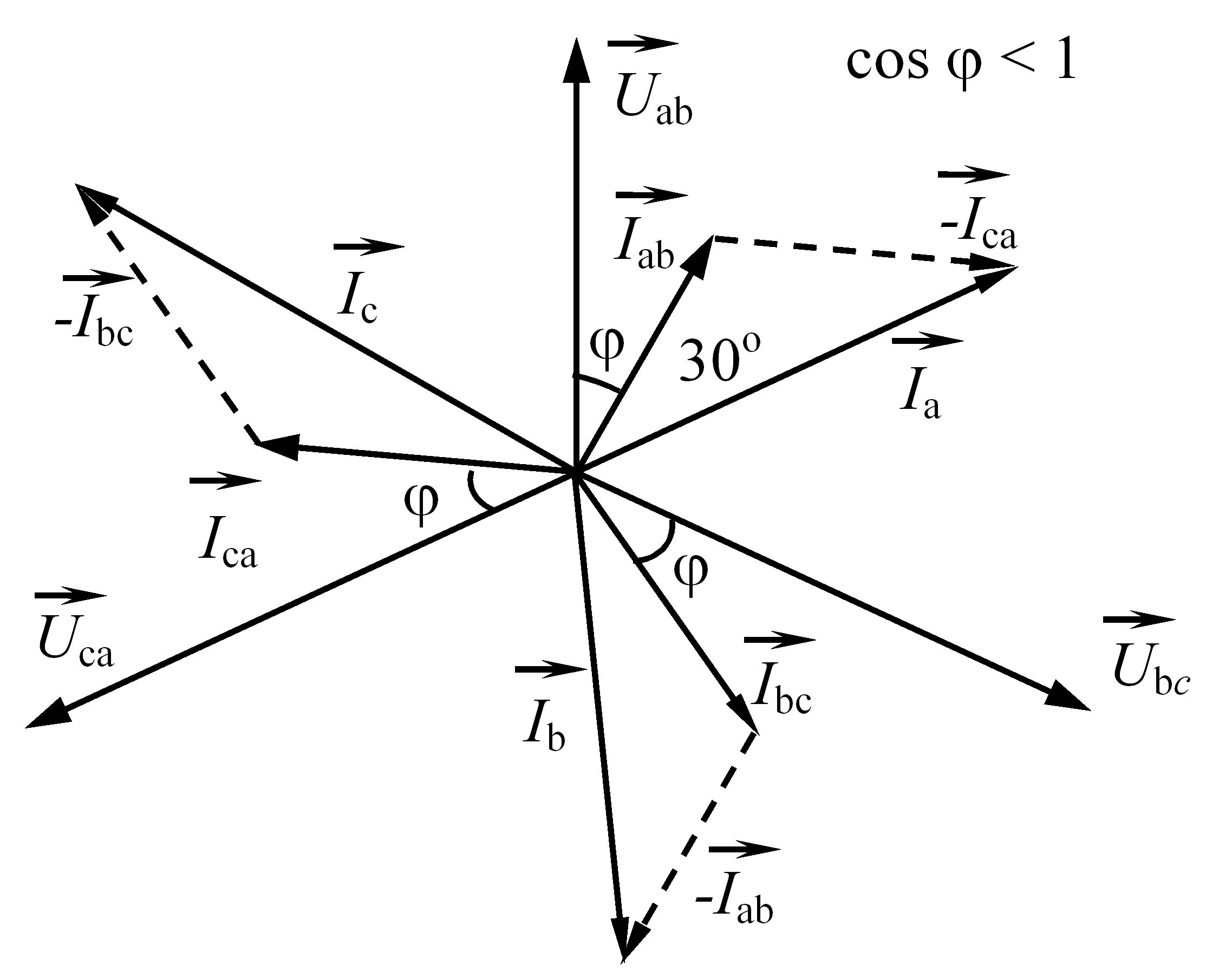
Рис. 3.53 – Векторна діаграма сил струмів і напруг для трифазного симетричного активно-індуктивного навантаження при з’єднанні споживачів трифазного струму "трикутником"

Несиметричне навантаження. Припустимо, що 

<<, φab = φbc = φca = 0.                                     (3.96)

Оскільки фазні напруги дорівнюють лінійним напругам, то вони залишаються незмінними. Тому сили фазних струмів за абсолютними значеннями за законом Ома будуть відповідати наступному співвідношенню:

>>.                                                                                                                                  (3.97)

Нерівність величин фазних струмів призводить до нерівності величин лінійних струмів, а також до нерівності кутів зсуву фаз між лінійними силами струмів і напругами.

Величини лінійних струмів визначаються з векторної діаграми так само, як і у випадку симетричного навантаження, але в цьому випадку співвідношення  виконуватися не буде.

При виконанні умови (3.96) маємо активне несиметричне навантаження, отже:

,      ,       .

Векторна діаграма сил струмів і напруг для несиметричного активного навантаження зображена на рис. 3.54.

Слід звернути увагу на те, що при з’єднанні трифазного споживача "трикутником" несиметричність фазних навантажень не призводить до несиметричності напруг у споживача, як це спостерігається при з’єднанні споживача "зіркою".

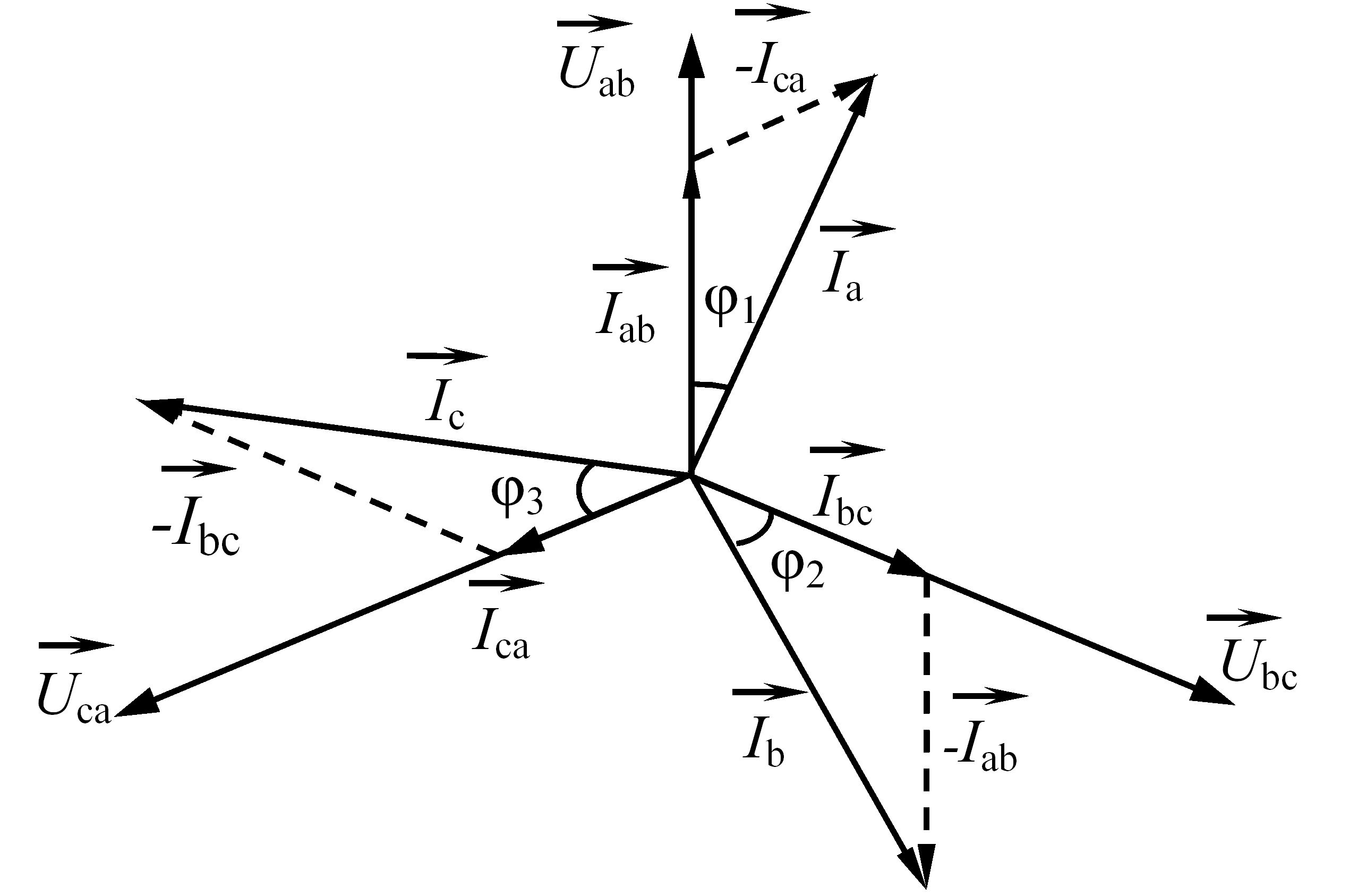
Рис. 3.54 – Векторна діаграма сил струмів і напруг для трифазного несиметричного активного навантаження при з’єднанні споживачів трифазного струму "трикутником"

Аналіз роботи кола з обривом одного з лінійних (фазних) провідників. Обрив одного з лінійних (фазних) провідників або спрацювання однополюсного апарата захисту (наприклад, плавкого запобіжника) в його колі призводить до перетворення схеми "трикутник" в однофазне розгалужене електричне коло. Такий режим роботи називається "неповнофазним" та є пожежонебезпечним. На рис. 3.55 приведено схему з’єднання споживачів трифазного струму "трикутником" при обриві лінійного (фазного) провідника С.

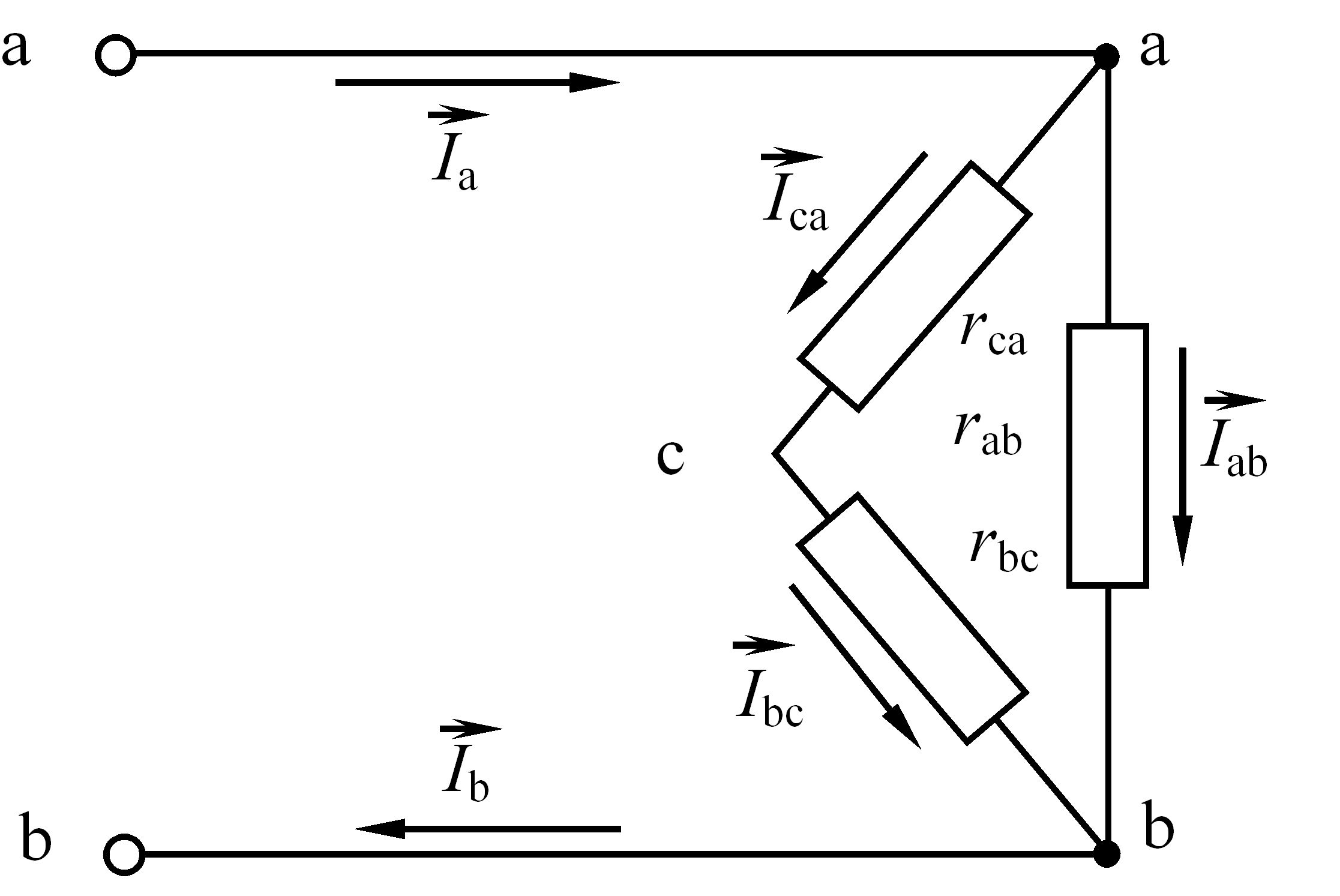
Рис. 3.55 – Схема з’єднання споживачів трифазного струму "трикутником" при обриві лінійного (фазного) провідника С

В одну вітку включений резистивний елемент з опором r ab . Сила фазного струму в ній залишається незмінною, тому що лінійна (фазна) напруга  не змінилася. 

У другу вітку включено два послідовно з’єднаних  резистивних елементи з опорами r ca  та r bc . Напруга на кінцях цієї вітки Uab, тому сили фазних струмів у цих резистивних елементах будуть рівними між собою:

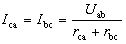  .                                              (3.98)

Позитивний напрямок струмів зображено на схемі стрілками. Отже, сили лінійних струмів визначаються як сума модулів сил фазних струмів: Ia = Iab + Ica , Ib= Iab + Ibc, але оскільки Ica = Ibc , то Ia = Ib.

Якщо r ca = r bc  (симетричне навантаження), то падіння напруги на цих резистивних елементах будуть однаковими і дорівнювати половині лінійної напруги:

.                                               (3.99)

Якщо r ca  > r bc, оскільки Ica = Ibc, то Ica ⋅ r ca > Ibc · r bc  та  Uca > Ubc , хоча Uca + Ubc = Uab.

Таким чином, обрив одного з лінійних (фазних) провідників призводить до зменшення напруги на тих двох фазах споживача, що підключені до цього провідника.

Обрив двох лінійних (фазних) провідників призводить до повного припинення роботи всіх трьох фаз споживача.