Електротехніка та пожежна профілактика в електроустановках

4.4 Перехідні процеси у колі синусоїдального струму з ємністю та активним опором.

Коло дослідження наведено на рис.3.27. До затискачів кола підключена синусоїдальна напруга:

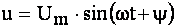                             ,                                                          (4.20)

де 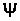- початкова фаза напруги.

У п. 3.5 вказано, що сталий струм такого кола синусоїдальний і випереджає напругу за фазою на кут φ:

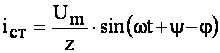                             ,                                               (4.32)

де ,

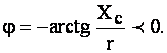
Стала напруга на затискачах конденсатора відстає за фазою від струму на кут :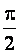

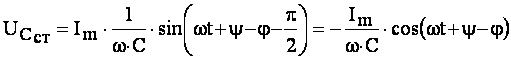. (4.33)

Вважаючи, що конденсатор попередньо не був заряджений, у момент вмикання напруга на його затискачах дорівнює нулю. Це можливо пояснити накладенням на сталу напругу вільної напруги, рівної та оберненої за знаком сталій напрузі. Тобто напругу на затискачах конденсатора можна розглядати як суму двох напруг - сталої та вільної:

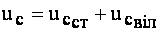                                           .                                                (4.34)

У момент вмикання 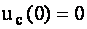та

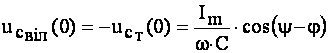     .                                            (4.35)

Струм кола буде:

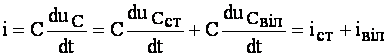        .                          (4.36)

Тобто струм і у цьому випадку включає дві складові - сталий струм та вільний струм.

Відповідно до другого закона Кірхгофа, можна записати для будь-якого моменту часу:

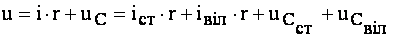                 .              (4.37)

При сталому режимі 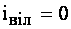та 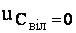. Тому (4.37) матиме вид:

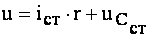                                     .                                                      (4.38)

Очевидно, з (4.37) та (4.38):

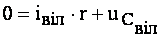                                     .                                                     (4.39)

Звідкіля

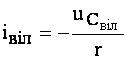                                       .                                                            (4.40)

Враховуючи, що

,

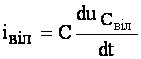одержуємо з (4.40) диференційне рівняння:

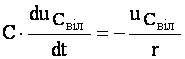                                   .                                                  (4.41)

Вирішуємо рівняння (4.41) методом поділу перемінних:

,   ,     ,

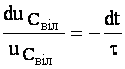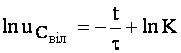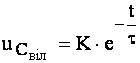                               ,                                                              (4.42)

де 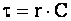- стала часу;

К - постійна інтегрування.

Постійна інтегрування К визначається з початкових умов:

- з (4.42): ;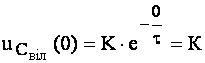

- з (4.35): .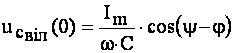

Остаточно вільна напруга на конденсаторі визначається за формулою:

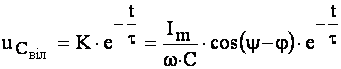             ,                                 (4.43)

а напруга на конденсаторі:

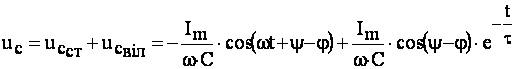.  (4.44)

Аналіз (4.44) показує, що на синусоїдальну сталу напругу накладається вільна напруга. Початкове значення вільної напруги залежить від фазових співвідношень (ψ та φ).

Якщо вмикання виникне у момент, коли стала напруга на конденсаторі проходить через нульове значення, то вільна напруга в колі не виникне. Це явище має місце при 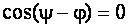або .

Якщо вмикання виникне у момент, коли стала напруга на конденсаторі проходить через максимальне значення, то початкове значення вільної напруги в колі також буде максимальне. Наприклад, вмикання виникло у момент, коли стала напруга на конденсаторі проходить через максимальне негативне значення (рис.4.6). Початкове значення вільної напруги в колі також буде максимальне та дорівнюватиме амплітуді сталої напруги 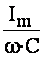. Це явище має місце при 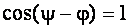або .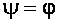

Рис.4.6 - Залежності u=f(t) при вмиканні до джерела кола з r та С ().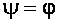

Оскільки знак сталої напруги періодично змінюється, а вільна напруга залишається увесь час позитивною, то через час, приблизно рівний половині періоду після вмикання кола, стала й вільна напруги будуть мати однаковий знак. Якщо за цей час вільна напруга зменшиться незначною мірою (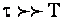), то найбільше значення напруги стане близьким до подвійної амплітуди сталої напруги на конденсаторі 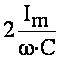. Цей ефект має тенденцію бути пожежонебезпечним, тому що можливий пробій ізоляції.

Залежність струму i=f(t) також визначається фазовими співвідношеннями.

З виразу (4.37) випливає:

,

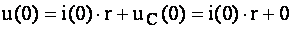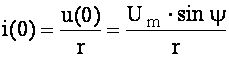                      .                                                    (4.45)

Якщо вмикання кола виникне у момент, коли напруга кола u максимальна, то початкове значення струму буде також максимальним:

                                              і_мах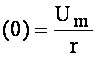 .                                                      (4.46)

Порівнюючи початкове значення струму з виразом на позначення амплітуди сталого струму

,

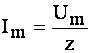бачимо, що за малих значень опору r, у порівнянні з z, початкове значення струму може бути у багато разів більше за амплітуду сталого струму, що являє собою пожежну небезпеку.

Вільна складова струму:

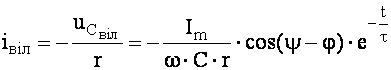         .                        (4.47)

Струм у будь-який момент часу:

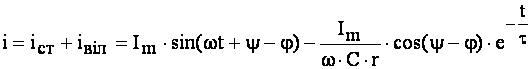(4.48)

Видно, що у початковій стадії процесу струм несинусоїдальний, а синусоїдальним стає через час приблизно 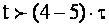(рис.4.7). Несинусоїдальність струму являє пожежну небезпеку для електротехнічних приладів, чутливих до якості струму живлення.

Рис.4.7 - Залежності і=f(t) при вмиканні до джерела кола з r та С ().

Питання для самоконтролю за темою "Перехідні процеси":

1. Порядок розв'язання диференціального рівняння, що описує перехідні процеси у колі постійного струму з реальною котушкою індуктивності.

2. Порядок розв'язання диференціального рівняння, що описує перехідні процеси у колі постійного струму з ємністю та активним опором.

3. Пожежна небезпека перехідних процесів в колі синусоїдального струму з реальною котушкою індуктивності.

4. Пожежна небезпека перехідних процесів в колі синусоїдального струму з ємністю та активним опором.

« 4.3 Перехідні процеси у колі синусоїдального струму з реальною котушкою індуктивності. Глава 5. Електричні машини та апарати. »