Аналітична форма. До цього ми використовували саме цю форму подання синусоїдальних величин, а саме
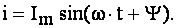(3.9)
Графічно ординати синусоїди у визначеному масштабі представляють миттєві значення величини, а абсциси – проміжки часу від початку рахування часу (рис.3.4.)
Рис.3.4 - Аналітична форма синусоїдальної величини
Таке подання дає можливість знайти амплітуду, початкову фазу і період синусоїдальної величини.
Складання (віднімання) двох синусоїдальних величин можна виконати графічно шляхом складання (віднімання) двох синусоїд, що зображують ці величини. Для одержання ординат сумарної кривої потрібно для кожного моменту часу скласти ординати кривих. Це виконано на рисунку 3.5.
Графічно складати (віднімати) можна синусоїдальні величини будь-якої частоти, амплітуди і початкової фази. При складанні двох синусоїдальних величин різної частоти створюється несинусоїдальна величина.
Рисунок 3.5 - Складання синусоїдальних величин
При складанні двох синусоїдальних величин однакової частоти створюється синусоїдальна величина тієї ж частоти.
У деяких випадках можливо складання (віднімання) синусоїдальних величин в аналітичній формі на основі тригонометричних формул.
Приклад: скласти дві величини
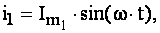
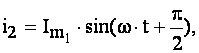
(Тобто різні тільки початкові фази).
Одержуємо:
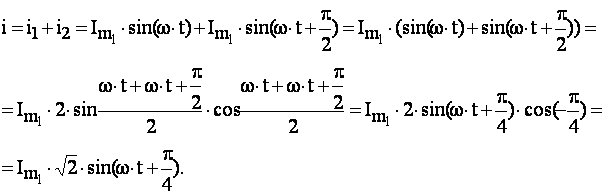
Векторна форма. Синусоїдальна величина може зображуватися вектором, що обертається. Довжина вектора в масштабі виражає амплітуду синусоїди. Кут, створений вектором з позитивним напрямком осі абсцис, у початковий момент часу дорівнює початковій фазі. Швидкість обертання вектора дорівнює кутовій частоті. Миттєві значення синусоїдальної величини виражаються проекціями вектора на вісь ординат. За позитивний напрямок обертання вибираємо обертання вектора проти годинної стрілки.
Векторною діаграмою називається сукупність векторів, що зображують декілька синусоїдальних величин однакової частоти в початковий момент часу.
Складання (віднімання) двох синусоїдальних величин можна проводити у векторній формі. При цьому складання (віднімання) векторів виконують за відомими геометричними правилами (правило трикутника, правило паралелограма).
Приклад (попередній приклад, але у векторній формі) виконаний на рис. 3.6. Довжина результуючого вектора
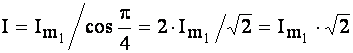
Рис.3.6 - Приклад складання синусоїдальних величину векторній формі.
Комплексними числами. Величина постійного струму визначається одним числом, величина змінного струму заданої частоти - двома числами (амплітуда і початкова фаза). Змінний струм може бути визначений і одним числом - комплексним.
Комплексним числом називається сума дійсного числа L і уявного (квадратний корінь з негативного числа), наприклад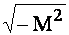 
. Уявне число 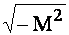подають у вигляді добутку дійсного числа М на квадратний корінь з негативної одиницї 
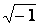, який називають "уявною одиницею" і позначають буквою j (або i):
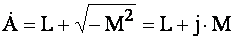. (3.10)
Дійсне число графічно подають відрізком на осі абсцис, а уявне - відрізком на осі ординат або вектором з початку координат у дану точку.
Існує:
1) алгебраїчна форма комплексних чисел :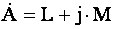 
;
2) тригонометрична форма комплексних чисел:
,
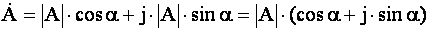де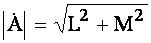 
- модуль, 
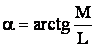- фаза.
3) показова форма комплексних чисел: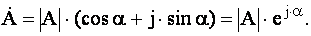
Комплексні числа додаються, віднімаються, множаться, діляться за правилами, відомими із вищої математики.
Приклад (попередній приклад у комплексній формі):
Струм з нульовою початковою фазою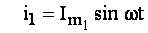
у комплексній формі має вид: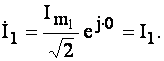
Домовимося амплітудою комплексного струму вважати його дійсне значення (часто амплітудою вважають і амплітудне значення). Точка над буквою позначає синусоїдальність величини.
Цей струм додається до струму тієї ж амплітуди, частоти, але з початковою фазою p/2:
.
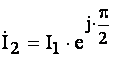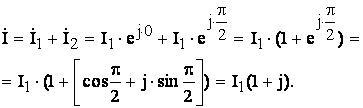
Миттєве значення струму:
.
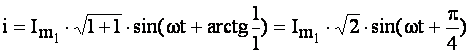Зображення синусоїдальних величин комплексними числами дозволяє значно спростити розрахунки кіл змінного струму. У цьому випадку говорять, що електричні кола розраховуються символічним методом.
| « 3.2 Принципи одержання синусоїдних ЕРС. | 3.4 Поняття індуктивності, взаємоіндуктивності, ємності. » |