|
|
Задачі, які розглянуті в 3.1, відносяться до класу задач геометричного проектування [61], у яких моделюється реальний процес розміщення об'єктів в областях і покриття об'єктами областей довільної просторової форми. При моделюванні здійснюється обробка і різні способи перетворення геометричної інформації. Для побудови математичної моделі розглянутої вище задачі необхідно побудувати математичну модель реальних об'єктів і областей розміщення (покриття), формалізувати взаємовідношення між ними (ввести обмеження) і представити в аналітичному вигляді критерії якості.
Як адекватна математична модель реального об'єкта (пожежного депо .jpg) ) розглядається клас точкових множин простору %201.jpg) , що задовольняють відповідним аксіомам [ 62 ]. , що задовольняють відповідним аксіомам [ 62 ].
Усякий геометричний об'єкт має просторову форму, має задані метричні характеристики, займає деяке положення в просторі %201.jpg) . Перераховані характеристики задають геометричну інформацію про об'єкт .jpg) [ 61 ]. Отже, геометрична інформація складається з трьох компонентів: [ 61 ]. Отже, геометрична інформація складається з трьох компонентів: .jpg) , де , де s.jpg) - сукупність просторових форм (опуклі, не опуклі багатокутники); - сукупність просторових форм (опуклі, не опуклі багатокутники); 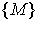 - метричні характеристики (координати вершин багатокутників у власній системі координат), що дозволяють відрізняти один об'єкт від іншого; - метричні характеристики (координати вершин багатокутників у власній системі координат), що дозволяють відрізняти один об'єкт від іншого; 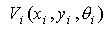 - параметри , що задають місце розташування об'єкта - параметри , що задають місце розташування об'єкта .jpg) в просторі в просторі %201.jpg) . Параметри . Параметри 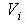 , що характеризують положення власної системи координат кожного об'єкта , що характеризують положення власної системи координат кожного об'єкта .jpg) щодо нуля простору, називаються “параметрами розміщення об'єктів”. щодо нуля простору, називаються “параметрами розміщення об'єктів”.
Іншими словами, кожен об'єкт, який задано трьома компонентами геометричної інформації, є математичною моделлю реального об'єкта. Розглянутий реальний об'єкт у цій роботі - пожежне депо має просторову форму - неопуклий багатокутник, типові проекти якого розрізняються метричними характеристиками (рис.1-10 додатка), характеризується параметрами розміщення.
У задачах, які розглянуто у 3.1, значення параметрів 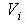 об'єктів обмежується областю розміщення. Область розміщення 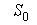 - це точкова множина простору - це точкова множина простору %201.jpg) , що задовольняє відповідним аксіомам [ 62 ]. Розглянемо компоненти геометричної інформації областей розміщення, які розглянуто у роботі. Область , що задовольняє відповідним аксіомам [ 62 ]. Розглянемо компоненти геометричної інформації областей розміщення, які розглянуто у роботі. Область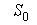 , задається трьома компонентами геометричної інформації , задається трьома компонентами геометричної інформації 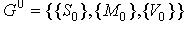 і є математичною моделлю матеріальних областей розміщення. Просторова форма і є математичною моделлю матеріальних областей розміщення. Просторова форма .jpg) може бути одно- зв’язною (район без областей заборони), багатозв’язною (район з областями заборони), незв'язною (набір районів), а компоненти може бути одно- зв’язною (район без областей заборони), багатозв’язною (район з областями заборони), незв'язною (набір районів), а компоненти і і 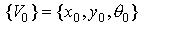 мають фіксовані значення. мають фіксовані значення.
Таким чином, область 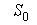 , задана трьома компонентами геометричної інформації , задана трьома компонентами геометричної інформації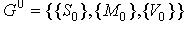 , є математичною моделлю матеріальних областей розміщення. , є математичною моделлю матеріальних областей розміщення.
Під пожежною зоною захисту розуміють область 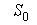 довільної просторової форми з існуючим у ній міським ландшафтом - сукупністю будинків (об'єктів розміщення) і вільних просторів, які обмежені будинками, вулицями, площами. У залежності від домінуючих типів об'єктів забудови розрізняють три види областей: житлову, промислову, змішану. Для двох видів зон - житлової і промислової - відповідно до прийнятої практики [ 63, 64 ] визначені по три незбіжних типів об'єктів - їхня класифікація приведена в таблиці 3.1. довільної просторової форми з існуючим у ній міським ландшафтом - сукупністю будинків (об'єктів розміщення) і вільних просторів, які обмежені будинками, вулицями, площами. У залежності від домінуючих типів об'єктів забудови розрізняють три види областей: житлову, промислову, змішану. Для двох видів зон - житлової і промислової - відповідно до прийнятої практики [ 63, 64 ] визначені по три незбіжних типів об'єктів - їхня класифікація приведена в таблиці 3.1.
Таблиця 3.1. – Більш докладна класифікація типів об'єктів
|
Тип пожежної зони |
Тип об'єкта |
Функціональна спрямованість будинків і споруджень |
| |
1 |
Житлові й адміністративні будинки |
|
Житлова |
2 |
Магазини, лікувальні установи і навчальні заклади |
| |
3 |
Видовищні, культурно-видовищні спорудження |
| |
4 |
Складські приміщення і торгові бази |
|
Промислова |
5 |
Виробництва категорії Б |
| |
6 |
Деревообробні і текстильні підприємства |
У змішаній зоні (промислово-житлового району), яка утворюється на основі сполучення великих житлових масивів і групи підприємств, що забезпечують досить широкий діапазон зайнятості населення, дислокуються всі шість типів об'єктів. У нормативній літературі [ 63,64 ] як зони захисту розглядаються різні кола, радіус яких нормується. Таким чином, як нормативну пожежну зону будемо розглядати деяку область 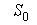 , просторова форма якої - коло, метричною характеристикою якої є нормований радіус, а параметри розміщення – фіксовані для існуючих об'єктів захисту.
Розглянемо обмеження, що накладаються на розміщення об'єкта .jpg) і задають область W припустимих розв’язків задачі. Ці обмеження включають:
1) умови взаємного не перетинання об'єкта .jpg) з областями заборони з областями заборони .jpg) (житловими будинками, будинками виробничого й обслуговуючого комплексу, дорогами, скверами і т.інш.) (житловими будинками, будинками виробничого й обслуговуючого комплексу, дорогами, скверами і т.інш.)
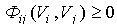 , ,
де 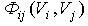 - Ф - функція [ 65 ], що має наступну характеристичну властивість: - Ф - функція [ 65 ], що має наступну характеристичну властивість:
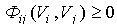 , якщо , якщо 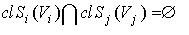 , ,
 , якщо , , якщо , 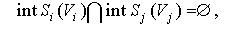 , ,
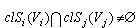 , якщо , якщо 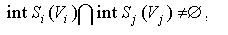 , ,
де .jpg) - замикання і внутрішність множини 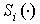 [ 66 ]. [ 66 ].
Характеристична властивість Ф - функції дозволяє говорити про перетинання, неперетинання і торкання об'єктів.
Якщо між об'єктами задані мінімально-припустимі відстані lit.jpg) , то умова взаємного неперетинання об'єктів  і і .jpg) з урахуванням заданих мінімальних відстаней, матиме вид: з урахуванням заданих мінімальних відстаней, матиме вид:
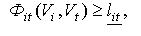
а у випадку, коли наявні й обмеження на максимальні відстані 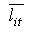 , умова взаємного неперетинання з обліком мінімальних і максимальних відстаней буде такою:
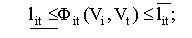
2) умови розміщення об'єкта  в області  (проектованому районі) з урахуванням припустимих відстаней від границі області (проектованому районі) з урахуванням припустимих відстаней від границі області 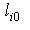 : :
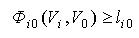 ; (3.3) ; (3.3)
3) додаткові протипожежні (технологічні) вимоги, що накладають додаткові обмеження на параметри розміщення і можуть бути формалізовані у виді деяких нерівностей :
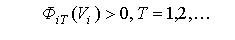 (3.4) (3.4)
Розглянемо критерії мети (якості) задач, що виникають на етапах середньострокового і поточного планування. На етапі середньострокового планування необхідно знайти таке розташування мінімальної кількості пожежних депо 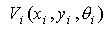 і визначити їхні типи, щоб разом із зонами захисту існуючих депо цілком покрити місто з районом, що проектується. На етапі поточного планування необхідно знайти таке розташування мінімальної кількості пожежних депо 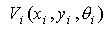 і метричні характеристики земельних ділянок під них, щоб з урахуванням неоднорідності території за вартістю, щільністю забудови, різної пожежної небезпеки будинків, різної характеристики магістралей і т.д. мінімізувати час досягнення пожежними підрозділами можливих осередків пожежі. Таким чином, у розглянутих задачах функція мети залежить від параметрів розміщення пожежного депо (об'єкта і метричні характеристики земельних ділянок під них, щоб з урахуванням неоднорідності території за вартістю, щільністю забудови, різної пожежної небезпеки будинків, різної характеристики магістралей і т.д. мінімізувати час досягнення пожежними підрозділами можливих осередків пожежі. Таким чином, у розглянутих задачах функція мети залежить від параметрів розміщення пожежного депо (об'єкта ) )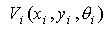 , тобто , тобто 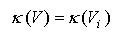 . .
На етапі середньострокового планування виникає наступна задача. Побудуємо її математичну модель.
Представимо місто у вигляді обмеженої області 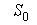 довільної просторової форми. Нову введену територію позначимо довільної просторової форми. Нову введену територію позначимо 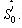 . Пожежне депо представимо у вигляді об'єкта захисту кругової зони , радіус r якої нормується, а значення . Пожежне депо представимо у вигляді об'єкта захисту кругової зони , радіус r якої нормується, а значення 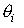 для кола надалі не будемо враховувати. Існуючі в місті депо позначимо для кола надалі не будемо враховувати. Існуючі в місті депо позначимо 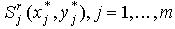 . .
Необхідно визначити мінімальну кількість n пожежних депо і параметри їхнього розміщення в області 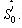 , що цілком покривають разом з об'єктами , що цілком покривають разом з об'єктами 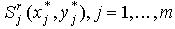 область область 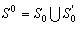 ,тобто ,тобто
.jpg) . (3.5) . (3.5)
Позначимо через 5.jpg) , i=1,...,n,j=1,...,m
( рис. 3.1).
Тоді умову (3.5) можна формалізувати як:
7.jpg)
де 8.jpg) - функція об'єктів - функція об'єктів 9.jpg) і і 10.jpg) . .
Таким чином, необхідно знайти
.jpg) , (3.6) , (3.6)
де 1.jpg) , а область 2.jpg) задається нерівністю задається нерівністю
3.jpg) (3.7) (3.7)
Побудуємо математичну модель задачі, що виникає на етапі поточного планування.
Нехай визначені архітектурне і планувальне рішення споруджуваного району (створений план його забудови типовими будинками, кількість типів - c). Представимо план забудови у виді деякого незв'язного об'єкта 1.jpg) кількість об'єктів t-того типу). Будинки за ступенем пожежної небезпеки, у залежності від речовин, що зберігаються в їхніх приміщеннях (табл.11 додатка), поділяються на кілька категорій. кількість об'єктів t-того типу). Будинки за ступенем пожежної небезпеки, у залежності від речовин, що зберігаються в їхніх приміщеннях (табл.11 додатка), поділяються на кілька категорій.
Для будинків категорій А, Б (табл.12 додатка) повинні бути витримані нормовані максимально-припустимі відстані 2 км із метою зменшення пожежного ризику [ 67 ]. До будинків інших
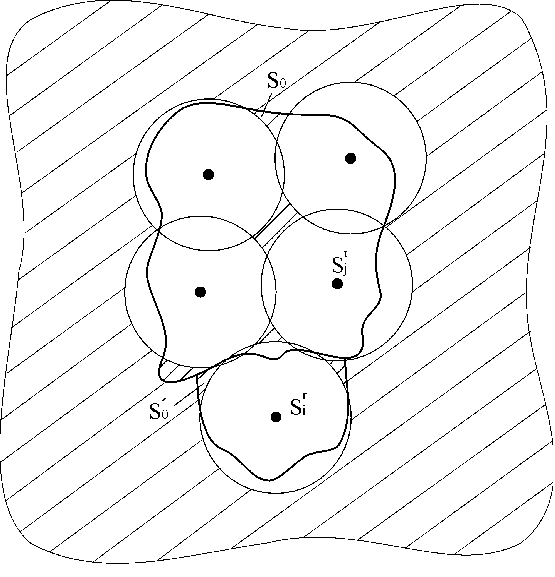
Рис. 3.1. Додаток області покриття до площини
категорій максимально-припустимі відстані становлять 3 км .
У проектованому районі можуть бути природні і штучні перешкоди - ріки, парки, залізні й автомобільні дороги, інженерні мережі. Представимо їх у виді деяких геометричних об'єктів 2.jpg) . Пожежне депо разом з відведеною для нього земельною ділянкою представимо у вигляді деякого геометричного об'єкта 3.jpg) , де m - тип об'єкта , де m - тип об'єкта 4.jpg) , що має свої метричні характеристики. Виникає задача визначення такого місця розташування , що має свої метричні характеристики. Виникає задача визначення такого місця розташування 5.jpg) об'єктів об'єктів 6.jpg) , їхньої орієнтації , їхньої орієнтації 7.jpg) і типу m в області і типу m в області 8.jpg) , що дозволяють скоротити час прибуття оперативних відділень до всіх можливих осередків пожежі. Час руху пожежних підрозділів від пожежних депо до можливих осередків пожеж залежить від багатьох факторів. Основний з них - відстань від депо c параметрами розміщення , що дозволяють скоротити час прибуття оперативних відділень до всіх можливих осередків пожежі. Час руху пожежних підрозділів від пожежних депо до можливих осередків пожеж залежить від багатьох факторів. Основний з них - відстань від депо c параметрами розміщення 9.jpg) до можливого осередку до можливого осередку 10.jpg) . На час руху також впливає ще цілий ряд факторів, перерахованих у 3.1. Перераховані обмеження можна об'єднати в групу технологічних обмежень. У розглянутій задачі наявні обмеження геометричного характеру: умови неперетинання об'єкта . На час руху також впливає ще цілий ряд факторів, перерахованих у 3.1. Перераховані обмеження можна об'єднати в групу технологічних обмежень. У розглянутій задачі наявні обмеження геометричного характеру: умови неперетинання об'єкта 11.jpg) з об'єктами з об'єктами 12.jpg) і і 13.jpg) з урахуванням заданих протипожежних мінімально і максимально-припустимих відстаней між ними й умов розміщення об'єкта з урахуванням заданих протипожежних мінімально і максимально-припустимих відстаней між ними й умов розміщення об'єкта 14.jpg) в області в області 15.jpg) . .
Таким чином виникає наступна задача.
Визначити такі параметри розміщення 16.jpg) об'єкта 14.jpg) і його тип (метричні характеристики), щоб скоротити час прибуття оперативних відділень до можливих осередків пожежі, тобто і його тип (метричні характеристики), щоб скоротити час прибуття оперативних відділень до можливих осередків пожежі, тобто
знайти
.jpg) , (3.8) , (3.8)
де 1.jpg) - мінімальний час руху від пожежного депо з параметрами розміщення 2.jpg) до можливого осередку пожежі до можливого осередку пожежі 3.jpg) , який витрачають оперативні відділення, на множині шляхів руху , який витрачають оперативні відділення, на множині шляхів руху 4.jpg) , яка складена з лінійних ділянок траси і перехресть; , яка складена з лінійних ділянок траси і перехресть;
5.jpg) - - область припустимих розв’язків, що описується:
.jpg) (3.9) (3.9)
.gif) , (3.10) , (3.10)
.gif) , (3.11) , (3.11)
.jpg) , (3.12) , (3.12)
які визначають, відповідно, умови неперетинання об'єкта 1(2).jpg) з областями заборони, умови розміщення об'єкта1(2).jpg) в області в області 2.jpg) , обмеження відповідного елемента вектора ресурсів R, додаткові технологічні протипожежні обмеження. Як складові елементи вектора ресурсів розглядаються: , обмеження відповідного елемента вектора ресурсів R, додаткові технологічні протипожежні обмеження. Як складові елементи вектора ресурсів розглядаються: 3.jpg) - вартість будівництва депо, - вартість будівництва депо, 4.jpg) - вартість будівництва додаткової дороги (у разі потреби), - вартість будівництва додаткової дороги (у разі потреби), 5.jpg) - вартість земельної ділянки, яку займає депо, - вартість земельної ділянки, яку займає депо, 6.jpg) - вартість прокладки додаткових газо - і водомереж та інших інженерних мереж. - вартість прокладки додаткових газо - і водомереж та інших інженерних мереж.
Таким чином, здійснена декомпозиція задачі (3.1) на задачі (3.2), (3.6-3.7),(3.8-3.12), що враховує годинні інтервали реалізації планів міста і функціональні особливості задачі.
|
|
|