|
|
Розглянемо задачу (3.8-3.12). Умови (3.9-3.10,3.12) записані за допомогою Ф - функцій. Ф- поверхня 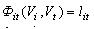 для пари об'єктів для пари об'єктів 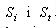 при заданому значенні при заданому значенні 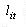 відома за назвою годографа функції щільного розміщення (г.ф.щ.р.) [ 71, 72 ]. Використовуючи цю властивість Ф - функції, область припустимих розв’язків задачі будемо будувати за допомогою математичного апарату годографа вектор - функції щільного розміщення об'єктів [71], що у даній роботі адаптований з урахуванням специфіки обмежень (3.9-3.12). відома за назвою годографа функції щільного розміщення (г.ф.щ.р.) [ 71, 72 ]. Використовуючи цю властивість Ф - функції, область припустимих розв’язків задачі будемо будувати за допомогою математичного апарату годографа вектор - функції щільного розміщення об'єктів [71], що у даній роботі адаптований з урахуванням специфіки обмежень (3.9-3.12).
Визначення 4.1. Об'єкти 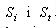 називаються “щільнорозташованими”, якщо найкоротша відстань між ними дорівнює заданій величині називаються “щільнорозташованими”, якщо найкоротша відстань між ними дорівнює заданій величині 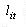 ( в окремому випадку ( в окремому випадку 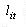 =0). =0).
Зафіксуємо положення об'єкта 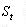 на площині, тобто його параметри розміщення 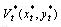 , і припустимо, що об'єкт , і припустимо, що об'єкт  може допускати довільні трансляції на площині. може допускати довільні трансляції на площині.
Визначення 4.2. Годограф вектора 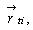 , що з'єднує полюси 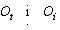 щільнорозташованих об'єктів щільнорозташованих об'єктів 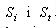 , називається “годографом вектор- функції щільного розміщення об'єктів”. , називається “годографом вектор- функції щільного розміщення об'єктів”.
Розглянемо геометричну інтерпретацію г .ф.щ.р. об'єктів 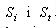 . .
Об'єкт  може допускати довільні трансляції на площині, залишаючись щільно розташованим стосовно об'єкта 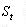 . Кінець вектора . Кінець вектора 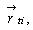 при зміні кута при зміні кута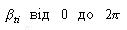 зробить повний оборот і опише на площині замкнуту лінію (годограф) (рис. 4.4). Величина зробить повний оборот і опише на площині замкнуту лінію (годограф) (рис. 4.4). Величина  є поточною відстанню між полюсами об'єктів є поточною відстанню між полюсами об'єктів 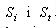 при будь-якому щільному їхньому взаємному положенні. при будь-якому щільному їхньому взаємному положенні.
Виходячи з геометричної інтерпретації г.ф.щ.р, можна дати інше його визначення.
Визначення 4.3. Годографом функції щільного розміщення об'єктів 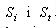 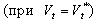 називається геометричне місце положень полюса називається геометричне місце положень полюса  об'єкта об'єкта  при його трансляції щодо об'єкта при його трансляції щодо об'єкта 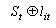 при виконанні умов: при виконанні умов: 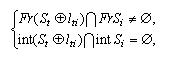
де 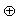 - сума Мінковського [73]; 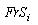 - границя об'єкта - границя об'єкта  , , 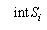 - внутрішня частина об'єкта - внутрішня частина об'єкта  . .
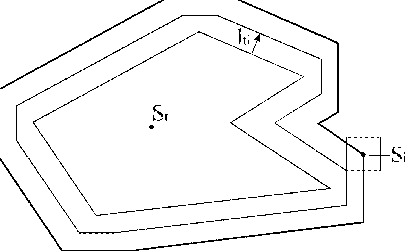
Рис. 4.4. Г.ф.щ.р. об ’єктів 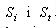

Рис. 4.5. Виконання умови 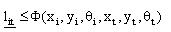 (побудова області можливих положень ПД з урахуванням мінімальних відстаней)
Нехай об'єкт 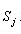 - незв'язний, тобто 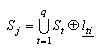 , а об'єкт , а об'єкт  - однозв'язний. - однозв'язний.
Твердження 4.1. Якщо об'єкт 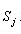 - незв'язний, а об'єкт - незв'язний, а об'єкт  - однозв'язний, то г.ф.щ.р. об'єктів - однозв'язний, то г.ф.щ.р. об'єктів 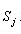 і і  є границя області є границя області 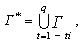 , де , де 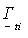 - область, границею якої є г.ф.щ.р. однозв'язних об'єктів - область, границею якої є г.ф.щ.р. однозв'язних об'єктів  . .
Наслідок. Г.ф.щ.р . незв'язного об'єкта 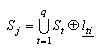 й однозв'язного об'єкта й однозв'язного об'єкта  є границя області є границя області 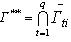 , де , де 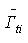 - область, границею якої є г.ф.щ.р. однозв'язних об'єктів - область, границею якої є г.ф.щ.р. однозв'язних об'єктів . .
Твердження 4.2. Для об'єктів 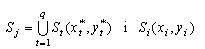 ліва частина нерівності (3.9) виконується, якщо параметри розміщення  належать множині належать множині 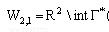 (рис.4.5), тобто (рис.4.5), тобто
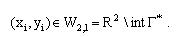 . .
Якщо об'єкти 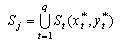 розглядати як будинки району, 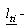 - як нормовані протипожежні відстані між ПД (об'єктом - як нормовані протипожежні відстані між ПД (об'єктом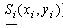 ) і будинками, то ) і будинками, то 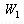 - область можливих значень параметрів розміщення ПД , що дозволяє реалізувати умови неперетинання ПД з областями заборони з урахуванням нормованих протипожежних відстаней. - область можливих значень параметрів розміщення ПД , що дозволяє реалізувати умови неперетинання ПД з областями заборони з урахуванням нормованих протипожежних відстаней.
Твердження 4.3. Для об'єктів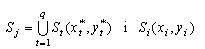 права частина нерівності (3.19) виконується, якщо параметри розміщення  належать множині належать множині 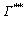 (рис.4.6), тобто (рис.4.6), тобто
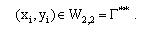 . .
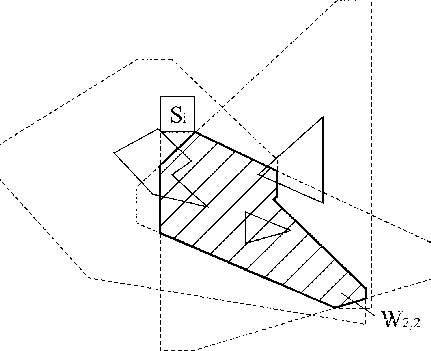
Рис. 4. 6. Виконання умови 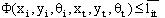 (побудова області можливих положень ПД з урахуванням максимальних відстаней) (побудова області можливих положень ПД з урахуванням максимальних відстаней)
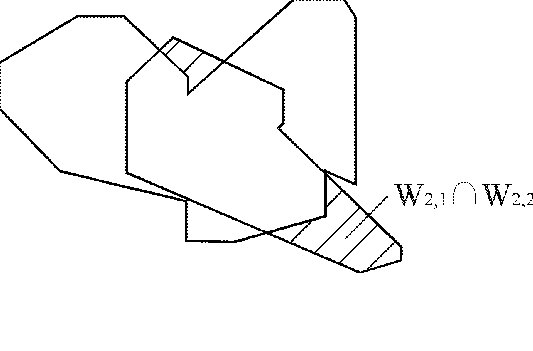
Рис. 4.7. Виконання умови 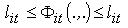 (побудова області можливих положень ПД з урахуванням максимальних і мінімальних відстаней)
Область 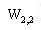 - множина можливих значень параметрів розміщення ПД , що визначає параметри розміщення ПД, що знаходяться від будинків 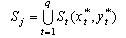 не далі, ніж максимальні припустимі відстані не далі, ніж максимальні припустимі відстані 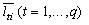 . Завданням максимальних припустимих відстаней здійснюється урахування різної пожежної небезпеки будинків і щільності забудови району. . Завданням максимальних припустимих відстаней здійснюється урахування різної пожежної небезпеки будинків і щільності забудови району.
Твердження 4.4. Умова (3.9) виконується (рис.4.7), якщо
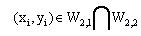 . .
Нехай 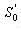 - довільна однозв'язна область, що має фіксовані параметри розміщення 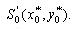 Об'єкт Об'єкт  може допускати довільні трансляції в області може допускати довільні трансляції в області 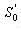 . .
Визначення 4.4. Внутрішнім г.ф.щ.р. 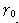 об'єкта  й області й області 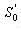 за фіксованих значень за фіксованих значень 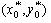 називається геометричне місце положень полюса називається геометричне місце положень полюса 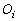 об'єкта об'єкта  при його трансляції в області при його трансляції в області 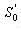 (рис.4.8) при виконанні умов [ 74 ]: (рис.4.8) при виконанні умов [ 74 ]:
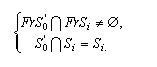
Твердження 4.5. Для однозв'язної області 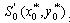 й об'єкта 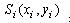 виконується умова (3.10) (рис.4.9), якщо справедливе співвідношення: виконується умова (3.10) (рис.4.9), якщо справедливе співвідношення:
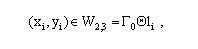 , ,
де  - область, границею якої є внутрішній г.ф.щ.р. 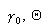 - різниця Мінковського [73]. - різниця Мінковського [73].
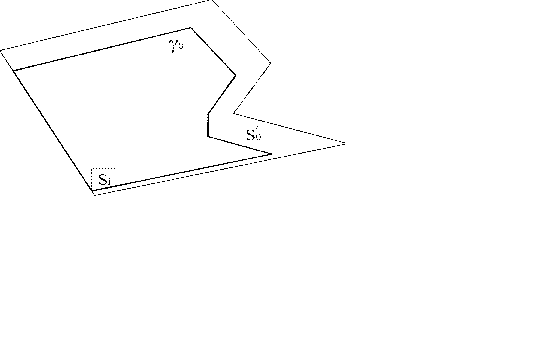
Рис. 4.8. Внутрішній г.ф.щ.р. об ’єкта  і області і області 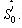 (побудова області можливих положень ПД в районі) (побудова області можливих положень ПД в районі)
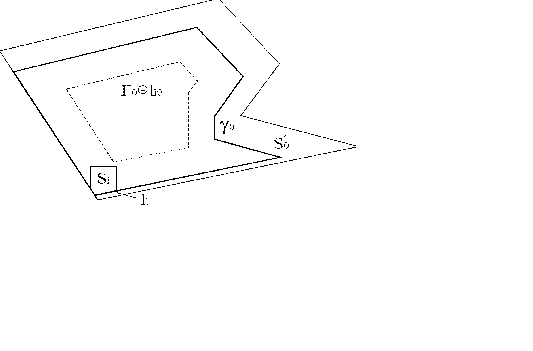
Рис. 4.9. Виконання умови 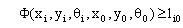 (побудова області можливих положень ПД в районі з урахуванням мінімальних відстаней)
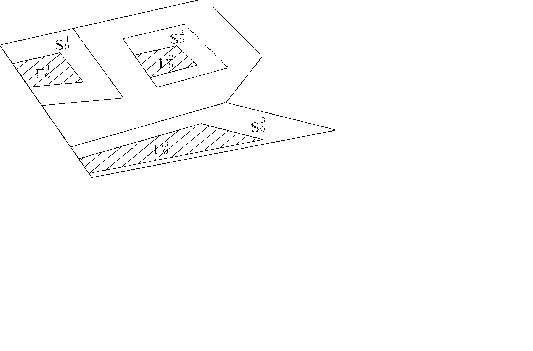
Рис. 4.10. Виконання умов 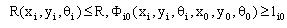 (побудова області можливих положень ПД з допустимою інвестаційною вартістю ділянок землі)
Якщо як район розглядати область 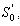 , а в якості ПД - об'єкт 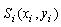 , то область , то область 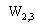 - область можливих значень параметрів розміщення ПД , що дозволяє реалізувати умови розміщення ПД у районі з урахуванням мінімальних нормованих відстаней - область можливих значень параметрів розміщення ПД , що дозволяє реалізувати умови розміщення ПД у районі з урахуванням мінімальних нормованих відстаней 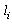 від границі району. від границі району.
Розглянемо формалізацію умови (3.11) за допомогою апарату г.ф.щ.р. Одним зі складових компонентів вектора обмеження ресурсів є вартість території під забудову 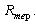 . Знаючи цю складову і площу земельної ділянки, необхідної для ПД (розраховану в 4.1), визначимо припустиму вартість 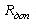 одного квадратного метра під забудову: одного квадратного метра під забудову: 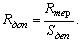 . Проаналізуємо область . Проаналізуємо область 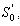 з погляду неоднорідності її території за вартістю. Виділимо такі ділянки області з погляду неоднорідності її території за вартістю. Виділимо такі ділянки області 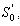 , для яких вартість 1м2 території (позначимо її , для яких вартість 1м2 території (позначимо її 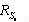 ) менше ) менше 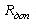 , тобто виконується: , тобто виконується:
.jpg) . (4.6) . (4.6)
Нехай у результаті визначиться r незв'язних підобластей 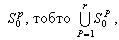 , для яких виконується умова (4.6). , для яких виконується умова (4.6).
Твердження 4.6. Для незв'язної області 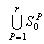 й об'єкта 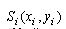 виконуються умови виконуються умови 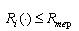 і і 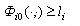 (рис.4.10), якщо справедливе співвідношення: (рис.4.10), якщо справедливе співвідношення:
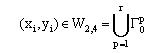 , ,
де 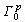 - область, границею якої є внутрішній г.ф.щ.р. області 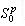 й об'єкта й об'єкта  . .
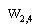 це область можливих значень параметрів розміщення ПД , що дозволяє реалізувати умови розміщення ПД у районі з урахуванням припустимої інвестиційної вартості. це область можливих значень параметрів розміщення ПД , що дозволяє реалізувати умови розміщення ПД у районі з урахуванням припустимої інвестиційної вартості.
Твердження 4.7. Умови (3.8-3.11) виконуються, якщо:
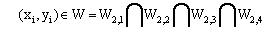 . .
Область W є областю припустимих розміщень об'єкта  з його постійними метричними характеристиками, що враховує умови неперетинання об'єктів з урахуванням мінімальних і максимальних припустимих відстаней, умови розміщення об'єкта в області й обмеження відповідного елемента вектора ресурсів за інвестиційною вартістю землі. Як показано в розділі 4.1, об'єкт з його постійними метричними характеристиками, що враховує умови неперетинання об'єктів з урахуванням мінімальних і максимальних припустимих відстаней, умови розміщення об'єкта в області й обмеження відповідного елемента вектора ресурсів за інвестиційною вартістю землі. Як показано в розділі 4.1, об'єкт  може мати різні припустимі метричні характеристики. У зв'язку з цим, використовуючи вищевикладені твердження 4.1-4.7, області може мати різні припустимі метричні характеристики. У зв'язку з цим, використовуючи вищевикладені твердження 4.1-4.7, області 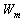 визначаються для кожного з об'єктів визначаються для кожного з об'єктів 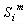 , коли m=1,2,...,M. Для об'єкта , коли m=1,2,...,M. Для об'єкта  з метричними характеристиками, що змінюються, як область, що задовольняє умовам (3.8-3.11) приймається область з метричними характеристиками, що змінюються, як область, що задовольняє умовам (3.8-3.11) приймається область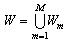 . Оскільки орієнтація об'єкта . Оскільки орієнтація об'єкта  вибирається щодо кожної з магістралей, то розглядається обмежений набір оріентацій об'єкта вибирається щодо кожної з магістралей, то розглядається обмежений набір оріентацій об'єкта 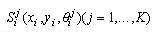 й обмеженням (3.8-3.11) буде задовольняти область й обмеженням (3.8-3.11) буде задовольняти область 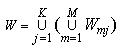 . .
Твердження 4.8. Якщо об'єкти 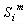 й область 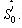 - багатокутні об'єкти довільної просторової форми, то область W - також багатокутна область довільної просторової форми [ 74 ]. - багатокутні об'єкти довільної просторової форми, то область W - також багатокутна область довільної просторової форми [ 74 ].
Характерною рисою області W є те, що для будь-якої точки цієї області (точки розміщення ПД) виконуються обмеження (3.8-3.11). ЯкщоW=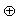 або обрана точка розміщення не влаштовує проектувальника з інших, технологічних розумінь (3.12), то проектувальник може в інтерактивному режимі вказати на інше місце розташування ПД. При цьому ПД може перетнути деякі об'єкти множини або обрана точка розміщення не влаштовує проектувальника з інших, технологічних розумінь (3.12), то проектувальник може в інтерактивному режимі вказати на інше місце розташування ПД. При цьому ПД може перетнути деякі об'єкти множини 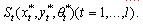 . Після виключення із системи обмежень названих об'єктів, знову, використовуючи перераховані вище обмеження, необхідно побудувати нову область W. Побудована область дозволяє визначати параметри розміщення об'єкта . Після виключення із системи обмежень названих об'єктів, знову, використовуючи перераховані вище обмеження, необхідно побудувати нову область W. Побудована область дозволяє визначати параметри розміщення об'єкта 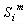 , що задовольняють перерахованим вище обмеженням. В умовах проектування виключені об'єкти множини , що задовольняють перерахованим вище обмеженням. В умовах проектування виключені об'єкти множини 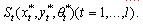 можна перерозмістити в проектованому районі, визначаючи область їхніх припустимих розміщень вищевикладеним способом, з урахуванням функції мети і додаткових обмежень містобудівництва. можна перерозмістити в проектованому районі, визначаючи область їхніх припустимих розміщень вищевикладеним способом, з урахуванням функції мети і додаткових обмежень містобудівництва.
|
|
|