МОДЕЛЮВАННЯ ДЕЯКИХ ПАРАМЕТРІВ СИСТЕМИ ПРОТИПОЖЕЖНОГО ЗАХИСТУ

4.1. Визначення раціональної нормованої кількості пожежних депо й їхніх типів для проектованого району міста

У 2.2 для формалізації розглянутих задач розміщення і покриття використовувався математичний апарат Ф- функцій. Ф- функції дозволяють природним чином записувати умови взаємного неперетинання об'єктів і умови їхнього розміщення в області для об'єктів, що допускають гладкість границь. Однак при формалізації умов покриття області необхідно розглядати сукупність об'єктів покриття, у результаті чого застосування апарату Ф- функцій стає неефективним, оскільки в даному випадку Ф- функція залежить від усіх перемінних параметрів розміщення об’єктів покриття, що характеризують цю сукупність. У зв'язку з цим для формалізації умов покриття застосуємо апарат w- функцій [ 68-69 ], де під w- функцією розуміють деяку ненегативну функцію, вимірну за Лебегом [ 66 ].

Формалізуємо за допомогою w- функцій умову покриття області  об’єктами  і (умови 3.5 чи 3.7). Нехай

 

Розглянемо поняття w- функцій на прикладі. Нехай  і  - кола радіуса r з параметрами розміщення  і , відповідно, і нехай . Тоді w- функція для кіл  і  однакового радіуса r буде мати вид:

 (4.1)

У виразі (4.1)  ( див. рис. 4.1) .

Тоді умова покриття області  матиме вид:

 .

Розглянемо особливості задачі покриття, що виникають на етапі середньострокового планування.

У місті існує множина з m пожежних депо з фіксованими параметрами розміщення . Кожне депо контролює зону радіуса r. Однак реальна схема розташування пожежних депо така, що не завжди цілком покриває область , тобто . Область S, у загальному випадку, незв'язна (див. рис.4.2). Задача покриття області , тобто прагнення до того, щоб , може виникнути тільки при оновленні міста, коли існуюча система депо не забезпечує пожежного захисту міста на належному нормованому рівні. У даній роботі ставиться задача визначення параметрів розміщення , що покривають область  , яка приєднується до міста, при умові .

Таким чином, необхідно визначити мінімальну кількість n пожежних депо і параметри їхнього розміщення  , тобто

 , (4.2)

 

 

 

 

 

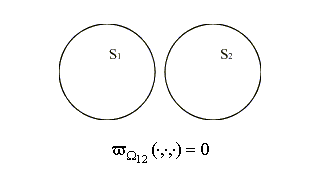
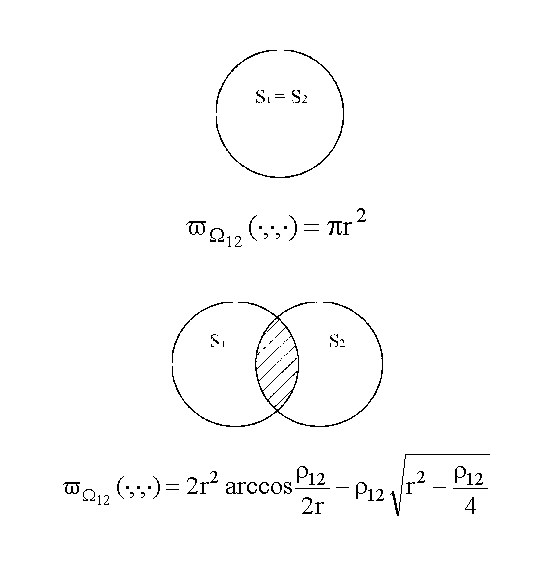
Рис. 4.1. w- функція для кол однакового радіуса

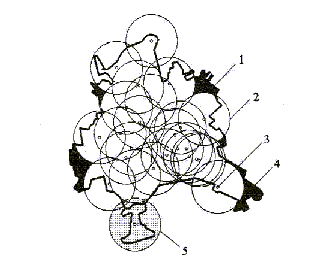
Рис. 4.2. Реальна схема покриття міста з новим районом, що приєднується до Харкова:

1 – границя міста Харкова;

2 – нормована кругова зона захисту;

3 – реальне місцезнаходження ПД;

4 – непокрита частина міста;

5 – кругова зона захисту Жихаря.

за умов

, (4.3)

. (4.4)

У розділі 3.2 показано, що задача (4.2-4.4) є багатоекстремальною. У зв'язку з цим процедура розв’язку полягає в пошуку локальних екстремумів функції мети і процедурі їхнього перебору. З огляду на той факт, що етап середньострокового планування є деякою завишеною нормативною оцінкою (верхньою оцінкою) для етапу поточного планування, а також у силу особливостей задачі (недиференційованості функції мети, неопуклості області її визначення) при обчисленні локальних екстремумів не слід прагнути до високої точності.

Для визначення локальних екстремумів використовується наближений метод послідовно-одиночного покриття [ 69 ]. Суть методу полягає в наступному. Мінімізація функції мети здійснюється по групах перемінних. У групу вибираються параметри розміщення одного покриваючого кола. Це дозволяє звести задачу мінімізації функції, яка задана в просторі 2n, до n- кратної оптимізації в 2-х вимірних просторах. Щоразу після розв’язку чергового етапу задачі оптимізації визначаються і фіксуються параметри розміщення покриваючого кола. Алгоритм реалізації методу послідовно-одиночного покриття можна записати у виді наступної ітераційної формули:

, (4.5) де 

На рис.4.3 приведені послідовно одержувані часткові покриття області  при розміщенні кіл .

У випадку, коли найбільше значення функції  досягається не в одній точці , а на множині точок, у якості  вибираються координати точки, що належить непокритій частині області  і для якої виконуються умови (4.4).

Метод послідовно-одиночного покриття дає можливість порівняно легко одержувати наближення до локальних екстремумів. Вибір місця розташування першого покриваючого об'єкта і порядок розміщення кіл однозначно визначають деяке наближення до локального екстремуму функції мети і відповідну точку в області припустимих розв’язків. Оскільки в роботі розглядаються кола рівного радіуса, то зміна порядку розміщення кіл не приводить до нового наближення до оптимуму. У зв'язку з цим, лише нове місце розташування першого покриваючого кола приводить до нового наближення до локального екстремуму.

Таким чином, можна установити відповідність між вибором місця розташування першого покриваючого кола і наближеннями до локальних екстремумів функції мети. Цей факт дає можливість розбити процес розв’язку задачі покриття на два етапи: визначення наближень до локальних екстремумів функції мети й організацію перебору одержуваних наближень. На першому етапі застосовується метод послідовно-одиночного покриття, на другому - методи їхнього перебору (повного - у випадку невеликої кількості покриваючих кіл і усіченого, що використовує особливості функціоналів, що оптимізуються, на комбінаторних множинах [ 69 ]).

Розв’язок задачі (4.2-4.4) дозволяє визначити кількість пожежних депо в проектованому районі.

Розглянемо тепер підхід до визначення типу пожежного депо. Для цього розглянемо одну з кругових зон , об'єктом захисту якої є пожежне депо. Потужність пожежного депо (кількість основних і спеціальних пожежних автомобілів), відповідно до нормативів визначається виходячи з чисельності населення, що проживає в зоні, яка захищається. Існують норми [ 70 ], що установлюють взаємозв'язок між чисельністю населення і кількістю пожежних автомобілів, необхідних для їхнього захисту. Ці норми зведені в таблиці 3-4 додатка [ 37 ].

Таблиця 3 додатка дозволяє визначити також нормовану площу земельної ділянки, що відводиться для одного пожежного депо.

 

 

 

 

Рис. 4.3. Послідовні часткові покриття кругами  довільної області

 

За таблицею 3, у залежності від чисельності населення K кругової зони, визначаємо нормовану чисельність населення , що обслуговує один автомобіль, а потім обчислюється кількість основних автомобілів з урахуванням 100% резерву :

Розрахунок необхідної кількості спеціальних автомобілів для розглянутої зони захисту здійснюється за допомогою нормативних даних, які приведені у таблиці 4 додатка.

Розрахувавши за таблицями 3-4 додатка кількість основних і спеціальних автомобілів і з огляду на вектор вартості  , виберемо проект пожежного депо (за кількістю пожежних автомобілів), і визначимо відповідні йому метричні характеристики. Визначимо габаритні розміри  ортогональної оболонки обраного проекту.

Пожежне депо повинно розміститися на земельній ділянці, площа якої  визначається з таблиці 3 додатка. Вибираємо . ПД повинно відступати на відстань метрів від краю ділянки, при цьому виїзд повинен бути таким, щоб ПА не перетинали основні потоки транспортних і людських магістралей. Промоделюємо форму і визначимо метричні характеристики земельної ділянки, що відводиться під пожежне депо. Нехай це буде прямокутник. Одна сторона цього прямокутника - це ,  - це відстань від ПД до границі земельної ділянки. Тоді інша сторона земельної ділянки визначається як ,  , 50 - це довжина в метрах тренувальної смуги з навчальною пожежною баштою. Збільшуючи величини  поки , визначимо набір прямокутників  з M різними метричними характеристиками, що надалі будемо розглядати як об'єкти розміщення. Нехай проект ПД є паралельним одній зі сторін прямокутника, тоді орієнтацію ПД і відповідно прямокутника (земельної ділянки) виберемо виходячи з умови, щоб ПА не перетинали транспортні потоки, тобто одна сторона прямокутника має бути паралельною дорозі, і зафіксуємо її для кожної з магістралей. Таким чином, будемо мати набір прямокутників , де K- кількість ділянок доріг з їх різним напрямком.

Таким чином, у 4.1 викладений підхід, що дозволяє для пожежного захисту проектованої області  визначити раціональну нормовану кількість пожежних депо n, їхнє місце розташування , вибрати типовий проект для кожного депо, розмір і набір можливих метричних характеристик земельної ділянки, що відводиться під забудову депо, а також для кожного депо визначити контрольовану ним кругову зону захисту.

© 2004 Академя гражданской защиты Украины