|
|
Розглянемо особливості задачі (3.6-3.7).
Функція мети 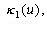 , у загальному випадку кусочно-гладка, причому нелінійна на кожній гладкій ділянці. Простір параметрів, у якому визначена функція мети, залежить від числа об'єктів n і має розмірність 2n. , у загальному випадку кусочно-гладка, причому нелінійна на кожній гладкій ділянці. Простір параметрів, у якому визначена функція мети, залежить від числа об'єктів n і має розмірність 2n.
2. Область припустимих розв’язків 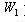 задається у виді однієї нерівності (3.7). Ця нерівність зв'язує всі параметри покриття кіл, що належать до неопуклої, багато зв’язної області припустимих розв’язків [67]. задається у виді однієї нерівності (3.7). Ця нерівність зв'язує всі параметри покриття кіл, що належать до неопуклої, багато зв’язної області припустимих розв’язків [67].
3. У силу нелінійності функції мети і неопуклості області її визначення, задача покриття, що розглянута в роботі, є багатоекстремальною. Екстремуми функції мети можуть знаходитися як усередині області припустимих розв’язків, так і на її границі.
Розглянемо особливості задачі (3.8-3.12).
Кількість нерівностей, що визначають область 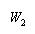 припустимих розв’язків (3.9-3.12), дорівнює q+l+1, де q- кількість нерівностей, що описують умови взаємного неперетинання об'єктів припустимих розв’язків (3.9-3.12), дорівнює q+l+1, де q- кількість нерівностей, що описують умови взаємного неперетинання об'єктів 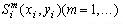 з областями заборони з областями заборони 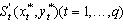 ; l- кількість нерівностей, що описують додаткові технологічні протипожежні вимоги, й одна нерівність, що описує умову розміщення об'єктів ; l- кількість нерівностей, що описують додаткові технологічні протипожежні вимоги, й одна нерівність, що описує умову розміщення об'єктів 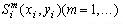 в області в області 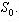 . .
Функції, що беруть участь у формуванні q+l+1 нерівностей (3.9 - 3.12), завжди нелінійні, у загальному випадку визначаються громіздкими трансцендентними виразами.
Область припустимих розв’язків (3.9 - 3.12) обмежена, неопукла, у загальному випадку незв'язна, кожна компонента її може бути багато-зв’язною.
Функція мети 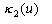 - час руху, який досліджується на множині шляхів руху - час руху, який досліджується на множині шляхів руху 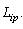 . Розглянемо її особливості більш детально. . Розглянемо її особливості більш детально.
Для цього мережу доріг представимо у вигляді графу 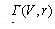 , де множина вершин V відповідає перехрестям, а множина ребер r - ділянкам доріг між перехрестями. На час руху по дорогах і через перехрестя впливає множина факторів, які перераховані вище, що характеризуються своєю неформалізованістю і які в моделі (3.8 - 3.12) об'єднані в групу технологічних обмежень (3.12). Нехай отримана узагальнена оцінка, що враховує ці фактори, у виді математичного сподівання часу руху 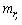 по кожній з ділянок доріг (ребру по кожній з ділянок доріг (ребру 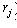 ) і математичного сподівання часу руху ) і математичного сподівання часу руху 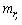 через кожне перехрестя (вершину через кожне перехрестя (вершину 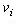 ). Помітимо, що вершинам відповідають також тупики й обривки доріг на границі області ( для них вага дорівнює 0). ). Помітимо, що вершинам відповідають також тупики й обривки доріг на границі області ( для них вага дорівнює 0).
Для спрощення моделі приймемо, що всі ділянки доріг прямолінійні і зробимо кусочно-лінійну апроксимацію нелінійних ділянок доріг. При цьому утвориться множина 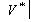 фіктивних перехресть з нульовою вагою 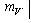 . .
Розглянемо задачу визначення максимального часу доступу для заданої точки p .
Можливі три випадки:
p збігається з однією з вершин 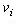 ; ;
p лежить на одному з ребер r, але не збігається з жодною з вершин;
pне збігається з жодною з вершин і не належить жодному з ребер.
Розглянемо спочатку перший випадок. Нехай p збігається з вершиною 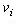 . Побудуємо множину . Побудуємо множину  шляхів l на графі d з вершин шляхів l на графі d з вершин 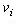 . У загальному випадку шлях l може бути заданий упорядкованим набором вершин графа Г, наприклад . У загальному випадку шлях l може бути заданий упорядкованим набором вершин графа Г, наприклад 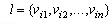 , а множину , а множину  - можна порахувати. Якщо ж виключити з розгляду шляхи з циклами, то множина шляхів l має деяку потужність N. - можна порахувати. Якщо ж виключити з розгляду шляхи з циклами, то множина шляхів l має деяку потужність N.
Для кожної з вершин 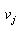 побудуємо множину у 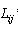 , що складається з усіх , що складається з усіх  , які ведуть у вершину , які ведуть у вершину 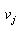 . Очевидно, що мінімальний час досягнення вершини . Очевидно, що мінімальний час досягнення вершини 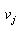 можна визначити за формулою можна визначити за формулою
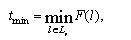
де F(l) - функція визначення часу руху по шляху l, який обумовлено як сума ваг усіх ребер і вершин, що входять у шлях.
Таким чином, час максимального доступу до вершини 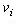 з вершини 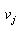 можна визначити як можна визначити як
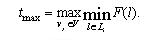 (3.13) (3.13)
Очевидно, що час доступу до будь-якої іншої точки , що належить ребрам графа Г, буде менше 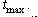 . .
Розглянемо другий випадок, тобто p належить деякому ребру 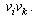 . У цьому випадку визначимо час . У цьому випадку визначимо час 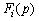 руху з p до вершини руху з p до вершини 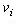 і час і час 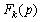 руху з точки p в вершину руху з точки p в вершину 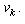 . .
Час доступу до найбільш віддаленої вершини 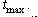 визначається за формулою:
.jpg) (3.14) (3.14)
Для випадку, коли p не належить ребрам графа Г і не збігається з жодною з її вершин, визначимо мінімальну відстань між точкою p і точкою 1.jpg) , що належить графу Г. , що належить графу Г.
Якщо 1.jpg) збігається з однією з вершин збігається з однією з вершин 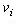 , то час доступу до найбільш віддаленого об'єкта визначається з (3.13) і збільшується на час , то час доступу до найбільш віддаленого об'єкта визначається з (3.13) і збільшується на час 2.jpg) руху з точки p в точку руху з точки p в точку 1.jpg) . .
Якщо ж1.jpg) належить одному з ребер, то діємо відповідно до формули (3.14), а результат також збільшуємо на 2.jpg) . .
Таким чином, аналіз особливостей розглянутих у роботі задач показує, що вони відносяться до класу задач нерегулярного розміщення і покриття геометричних об'єктів зі складною системою обмежень.
Розробці математичного, алгоритмічного і програмного забезпечення розглянутих у роботі задач присвячені наступні розділи даної роботи.
|
|
|