|
|
Розглянемо задачу, розв’язання якої складає основу більшості технологій пожежогасіння. Нехай струмінь води під певним напором Н виходить з пожежного ствола під кутом a до горизонту. Нехтуючи опором повітря, необхідно скласти рівняння струменя. Для простоти аналітичних виразів віднесемо початок координат до зрізу стовбура і направимо вісь Ох горизонтально (рис. 1.1). Також знайдемо дальність польоту струменя, висоту підйому і кут, при якому дальність польоту струменя досягає свого найбільшого значення.
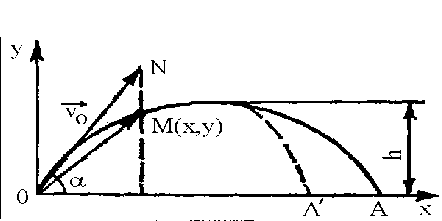
Рис.1.1 - Траєкторії руху частки води без урахування опору повітря (суцільна лінія) та з урахуванням (пунктирна лінія)
Виділимо в струмені частку води одиничної маси. Якби на неї не діяла сила ваги, то за час t вона пройшла б шлях, рівний модулю вектора ON (P,Q), де Р = v0tcos a , Q = v0tsin a , v0 — початкова швидкість частки.
Під дією сили ваги виділена частка пройде шлях, що дорівнює довжині дуги ОМ. Оскільки сила ваги спрямована вертикально вниз, то радіус-вектор ОМ (х, у) частки на вісь Ох буде мати таку ж проекцію, як і вектор ON, тобто х = v0t cos a , a проекція на вісь Оу буде на (gt2)/2 менше, тобто у = vat sin a - (gt2)/2.
Рівняння
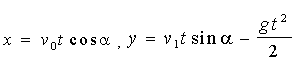 (1.1) (1.1)
є параметричними рівняннями траєкторії польоту частки.
Виключимо із першого рівняння параметр 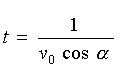 і, підставляючи його в друге рівняння, одержимо і, підставляючи його в друге рівняння, одержимо
 , (1.2) , (1.2)
де a = tg a ;
b = (g sec2 a )/2v02.
Як бачимо, траєкторія руху виділеної частки, а значить весь струмінь, має форму дуги параболи (нагадаємо, що опором повітря ми поки що нехтуємо).
Початкова швидкість частки визначається за формулою:
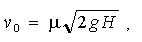
, (1.3)
де m — безрозмірний коефіцієнт, що залежить від форми насадки на отворі ствола;
Н — напір водяного стовпа (у метрах). Для конічних насадок, що сходяться, можна припускати m = 0,95.
Позначивши в рівнянні траєкторії руху виділеної частки у = 0, знайдемо дальність польоту струменя:
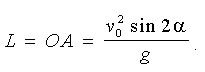 (1.4) (1.4)
Дальність польоту досягає свого найбільшого значення при a = 45°.
Висоту підйому струменя знайдемо з її рівняння при x = L/2
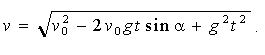 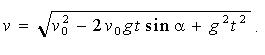 . (1.5) . (1.5)
Внаслідок опору повітря, частки води фактично рухаються не по параболі, а по кривій, зображеній на рис. 1.1 пунктиром. Тому на практиці найбільша дальність польоту струменя обчислюється за емпіричною формулою
L = 0.42Н + 1000 d, (1.6)
де d — діаметр вихідного перетину насадки в метрах, і досягається вона при a » 32°.
Вище було показано, що без врахування опору повітря і внутрішнього тертя струмінь води, що виходить з насадки стовбура під кутом a до горизонту, рухається за законом, який описано формулами (1.1). Визначимо величину швидкості струменя в довільний момент часу, а також у момент удару струменя об землю.
Для цього знову виділимо в струмені води елементарну частку. Траєкторія її польоту також описується параметричними рівняннями (1.1). Вектор швидкості v руху частки в довільний момент часу t спрямований по дотичній до траєкторії. Величини vx і vy складових вектора швидкості по осях координат Ох і Оу дорівнюють відповідно похідним від функцій x(t) і y(t) за часом t:
vx = v0 cos a , vy = v0 sin a - gt. (1.7)
Величину v швидкості руху частки, а значить і струменя, у довільний момент часу t знайдемо як геометричну суму величин її складових vx і vy:
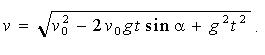 . (1.8) . (1.8)
Момент удару струменя об землю знайдемо з умови у = 0, що дає
t0 = (2y0 / g) sin a . (1.9)
Підставляючи знайдене значення t0 у вираз для v, знайдемо величину швидкості струменя в момент його удару об землю:
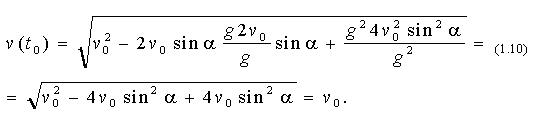
Таким чином, ми одержали цікаву властивість руху струменя води: величина швидкості струменя у момент його удару об землю дорівнює величині початкової швидкості струменя, при якій вона залишає пожежний ствол (незалежно від кута нахилу ствола).
53
|
|
|