|
|
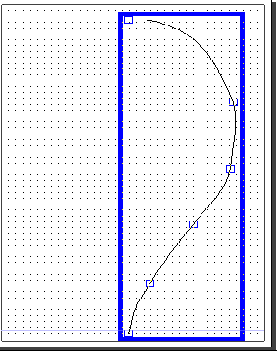
Дослідження фахівців та безпосередні спостереження показують, що існують принаймні чотири типові форми факелів полум’я, які виникають при аваріях на газопроводах. Будемо вважати, що факел полум’я обмежено поверхнею обертання. Умовно види таких факелів будемо називати “краплеподібним”, “еліпсоїдом”, “ліхтариком” та “грибоподібним”. На рис. 5.7 – 5.10 наведено зображення факелів та їх контурів, що є твірними відповідних поверхонь обертання.
|

|
|
|
а |
б |
Рис. 5.7 - “Краплеподібний” факел полум’я (а)
та крива як твірна поверхні обертання (б)
|

|
|
|
А |
б |
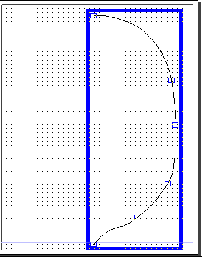
Рис. 5.8 - Факел полум’я “еліпсоїд” (а)
та крива як твірна поверхні обертання (б)
|

|
|
|
а |
б |
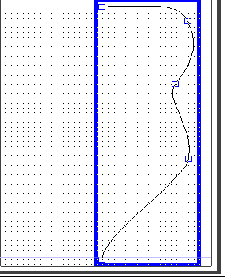
Рис. 5.9 - Факел полум’я “ліхтарик” (а)
та крива як твірна поверхні обертання (б)
|

|
|
|
А |
б |
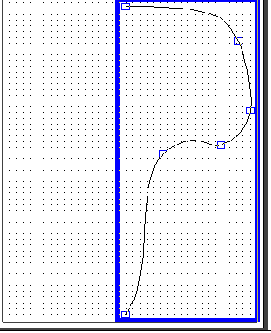
Рис. 5.10 - “Грибоподібний” факел полум’я (а)
та крива як твірна поверхні обертання (б)
Як приклад наведемо схему опису факела “краплеподібної” форми. Будемо вважати, що маємо фотографію певної “фази” факела. Окреслимо реальну твірну поверхні обертання, яку далі будемо називати профілем факела. На зображення профілю факела нанесемо декартову систему координат (рис. 5.11) і визначимо координати опорних точок.
Оскільки при обранні профілю факела матиме місце деяка похибка, пов’язана з суб’єктивним фактором, то для опису профілю можна використати поліноми. При цьому фактор осциляції на кінцевий результат не вплине, адже в результаті обчислень будуть визначатися інтегральні параметри променевої теплопередачі.
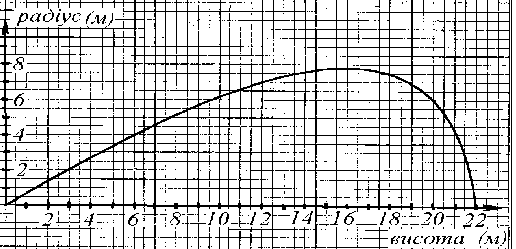
Рис. 5.11 - Профіль факела у декартовій системі координат
У розглянутому прикладі опорними будуть точки, рівновіддалені по висоті (з кроком 1 од.), у яких радіус кола (що у перерізі) матиме значення
R0:= 0: R1:= 0.8: R2:= 1.4: R3:= 2: R4:= 2.7:
R5:=3.4: R6:= 4: R7:= 4.5: R8:=5.2: R9:=5.8:
R10:=6.2: R11:=6.5: R12:=7: R13:=7.4: R14:=7.5:
R15:=7.7: R16:=7.8: R17:=7.7: R18:=7.5: R19:=7:
R20:=5.7: R21:= 4: R22:= 0:
Для аналітичного опису контуру поліномом використаємо програму leastsquare з бібліотеки stats математичного процесора Maple V (рис. 5.12). Вплив степеня полінома при описі профілю можна простежити за допомогою складеної програми. При цьому результатом роботи програми буде аналітичний вираз поліному та сумісне зображення двох профілів – апроксимованого та побудованого за допомогою вузлових точок.
|
restart: with(plots): with(plottools): with(stats):
prof[1]:= 0.8: prof[2]:= 1.4: prof[3]:= 2:
prof[4]:= 2.7: prof[5]:=3.4: prof[6] := 4:
prof[7] := 4.5: prof[8]:= 5.2: prof[9]:=5.8: prof[10]:=6.2: prof[11]:=6.5: prof[12]:=7: prof[13]:=7.4: prof[14]:=7.5: prof[15]:= 7.7:
prof[16]:=7.8: prof[17]:=7.7: prof[18]:=7.5: prof[19]:=7: prof[20]:=5.7: prof[21]:= 4:
prof[22]:= 0: prof[0]:= 0:
grik := curve([seq([i,prof[i]],i=0..22)], thickness=4):
pnts:= [seq(i,i=0..22)],[seq(prof[i],i=0..22)];
Rt := fit[leastsquare[[x,y],
y=a4*x^4+a3*x^3+a2*x^2+a1*x+a0]] ([pnts]):
R := evalf(rhs(Rt));
poli := plot(R(x),x=0..23, thickness=2):
display(grik,poli,axesfont=[TIMES,ITALIC,22]); |
Рис. 5.12 - Програма визначення аналітичного виразу
полінома для опису профілю факела
На рис.5.13 – 5.15 наведено приклади виконання програми (товстою лінією позначено початковий профіль). При цьому поліноми мають dbl^
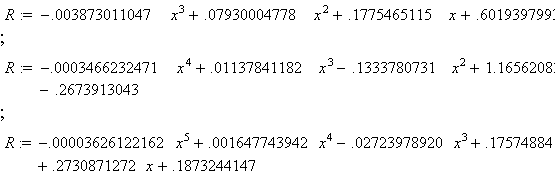
Легко переконатися, що задовільно описати профіль факела можна поліномом четвертого степеня (як поліномом мінімального степеня). Інші оцінки опису (крім візуальної) розробляти не варто, адже предметjv опису є поверхня факела як множина точок з нечіткою границею (“хмарою” плазми).
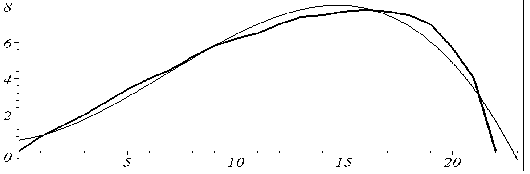
Рис. 5.13 - Порівняння профілів для кубічного полінома
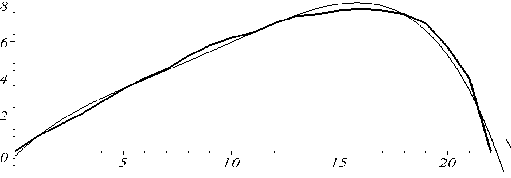
Рис. 5.14 - Порівняння профілів для полінома четвертого степеня
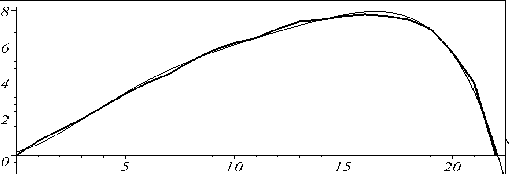
Рис. 5.15 - Порівняння профілів для поліномf п’ятого степеня
|
|
|