|
|
У попередніх розділах було розглянуто два на перший погляд віддалених одне від одного питання: опис графічного зображення певної фази розвитку гетерогенної системи речовин рівнянням у неявному виді F(x, y) = 0 та метод складання алгоритму чисельної екстраполяції функції за межами інтервалу, доступного для дослідження цієї функції. Далі ми поєднаємо ці питання у виді методу іміджевої інтерполяції та екстраполяції.
Якщо визначати коротко, то запропонований метод дослідження гетерогенних систем полягає у заміні в інтерполяційній схемі вузлових значень функції на вузлові зображення певних фаз розвитку у часі гетерогенної системи речовин. Тобто в роботі запропоновано метод відновлення проміжних зображень геометричного прояву гетерогенного процесу за вузловими зображеннями його певних фаз.
Раніше вже наголошувалося, що в даній роботі йтиметься лише про двокомпонентні гетерогенні системи, де графічним проявом реакцій буде сім’я роздільних поверхонь, перетином якої є сім’я роздільних кривих.
Прикладом вивчення гетерогенних систем речовин є дослідження геометричного прояву процесу вигоряння рослинного матеріалу при лісових пожежах. При цьому актуальними є дві задачі. Перша задача полягає у відновленні проміжних зображень геометричних форм (тобто сім’ї роздільних кривих) за вузловими зображеннями. Друга задача полягає у передбаченні (прогнозуванні) розвитку виявлених фаз гетерогенної системи у наперед заданий момент часу.
Пояснімо сказане на тривіальному прикладі лінійної іміджевої екстраполяції. При цьому “значення функції” у вузлових точках будуть зображеннями (тобто образами), звідси зрозуміло, чому запропонований метод названо "методом іміджевої інтерполяції" (image - зображення, образ).
Формула для лінійної інтерполяції має вид [51]:
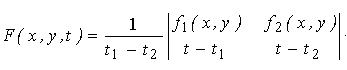 . (6.9) . (6.9)
Легко переконатися у тому, що виконуються тотожності F(x, y, t1) = f1 (x, y) i F(x, y, t2) = f2 (x, y), отже, формулу (3.21) можна використовувати і для іміджевої інтерполяції.
Розглянемо задачу визначення “динаміки” переходу форми розподільчої кривої гетерогенного процесу від квадрату до кола, рівняння яких є описами вузлових зображень в умовні моменти часу t1= 1 та t2 = 2:
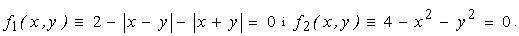 . (6.10) . (6.10)
Для цього складемо Maple-програму іміджевої поліноміальної екстраполяції
|
restart:with(plots): LAG := 0:
T[1] := 1: T[2] := 2:
F[1] := 2 - abs(x-y) - abs(x+y):
F[2] := 4 - x^2 - y^2:
G1 := implicitplot(F[1](x,y),x=-3..3,y=-3..3,
grid=[50,50], scaling=CONSTRAINED, thickness=3):
G2 := implicitplot(F[2](x,y),x=-3..3,y=-3..3,
grid=[50,50], scaling=CONSTRAINED, thickness=3):
for k from 1 to 2 do s := 1:
for j from 1 to 2 do if (k <> j) then
s := s*(t-T[j])/(T[k]-T[j]):
end if: end do:
LAG := LAG + s*F[k]: end do;
for i from 0 to 10 do
t := 1+2*i/10:
GR[i] := implicitplot(LAG(x,y),x=-3..3,y=-3..3,
grid=[50,50], scaling=CONSTRAINED):
if (t=3) then
G3 := implicitplot(LAG(x,y),x=-3..3,y=-3..3,
grid=[50,50], scaling=CONSTRAINED, thickness=3):
end if:
end do:
display({seq(GR[i],i=0..10),G1,G2,G3},
scaling=CONSTRAINED);
|
У результаті виконання цієї програми буде знайдено опис сім’ї кривих, елементи якої збігаються з інтерполяційними та екстраполяційними кривими. Дійсно, для обраного випадку на основі інтерполяційної формули одержимо рівняння:
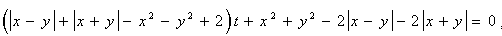 , (6.11) , (6.11)
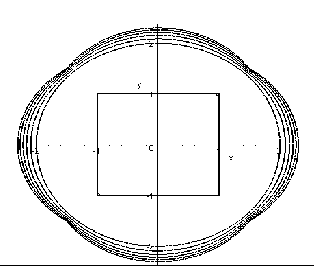
де параметр t змінюється у межах 1 £ t £ 2. На рис. 6.4 зображено множину роздільних кривих, що описані рівнянням (6.11) для деякої кількості фіксованих значень t, i що будуть проміжними між квадратом та колом.
Формулу (6.11) при t > 2 можна також використати як опис екстраполяційних кривих по відношенню до “вузлових” зображень квадрата та кола. Дійсно, наприклад, при t = 3 маємо рівняння екстраполяційної кривої у виді:
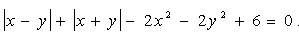 . (6.12) . (6.12)
На рис. 6.5 наведено зображення сім’ї екстраполяційних кривих, зовнішню з яких описано рівнянням (6.12). Порівнюючи рис. 6.4 і рис. 6.5, бачимо, що “відстань” між елементами сім’ї зменшується в залежності від збільшення параметра t, що є недоліком “прямого” використання відомої інтерполяційної формули.
|

|
|
|
Рис. 6.4 - Сім’я інтерполяційних кривих |
Рис. 6.5 - Сім’я екстраполяційних кривих |
Це спостереження вказує на те, що для іміджевої інтерполяції вузлові зображення необхідно описувати за допомогою нормальних рівнянь. Для цього, наприклад, рівняння (6.11) слід замінити на
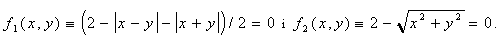 . (6.13) . (6.13)
Тоді для опису проміжних кривих матимемо рівняння:
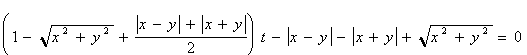 . (6.14) . (6.14)
У цьому випадку для t = 3 маємо рівняння екстраполяційної кривої
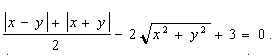 . (6.15) . (6.15)
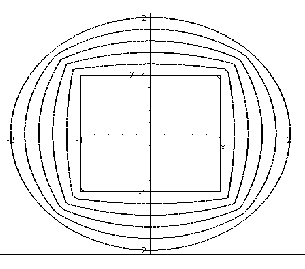
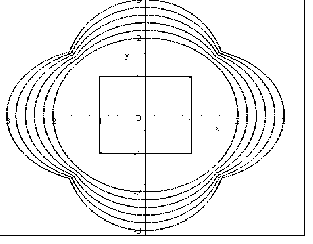
На рис. 6.6 та 6.7 наведено зображення сім’ї, відповідно, інтерполяційних та екстраполяційних кривих, зовнішню з яких описано рівнянням (3.27).
|
|
|
|
Рис. 6.6 - Сім’я інтерполяційних “рівновіддалених” кривих |
Рис. 6.7 - Сім’я екстраполяційних “рівновіддалених” кривих |
Пояснити необхідність використання нормальних рівнянь можна так. У тривимірному просторі Oxyt формула іміджевої інтерполяції є рівнянням поверхні W, нормальні перетини якої площинами t = 1 та t = 2 будуть мати вид, відповідно, квадрата та кола. Причому вибір опису цих кривих призводить до того, що довільна площина, дотична до поверхні W, буде нахилена до площини Oxy під кутом 45° (таку поверхню називають "поверхнею однакового схилу"). Останнє сприяє тому, що проекції сім’ї перетинів поверхні W площинами рівня t = const, розташованими на рівних відстанях, будуть “рівновіддаленими”.
Програма побудови поверхні W має вид
|
restart:with(plots):
T[1] := 1: T[2] := 2:
F[1] := (2 - abs(x-y) - abs(x+y))/2:
F[2] := 2 - sqrt(x^2 + y^2):
LAG := (-t+2)*F[1]+(t-1)*F[2];
implicitplot3d(LAG(x,y,t),x=-3..3,y=-3..3,t=1..3);
|
На рис. 6.8 наведено результат виконання програми - зображення різних ракурсів поверхні однакового схилу W.
Рис. 6.8 - Поверхня однакового схилу
Розглянемо інші приклади лінійної іміджевої екстраполяції. Нехай рівняння шестикутника, кола та квадрата мають вид:
f1 = 2Ö ` 3 - 2½ y½ - ½ y - xÖ ` 3½ - ½ y + xÖ ` 3½ ;
f 2 = 2,25 - x 2 -y 2; f3 = 3 -½ x - y½ -½ x + y½ . (6.16)
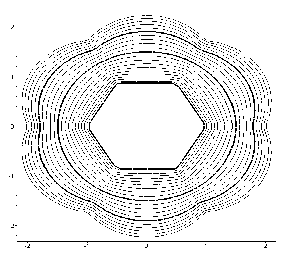
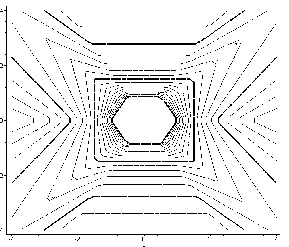
На рис. 6.9 – 6.10 наведено лінійні екстраполяції в умовні моменти часу t = 1 i t = 2 для випадків “шестикутник у колі” та “шестикутник у квадраті”.
|
|
|
|
Рис.6.9 - Шестикутник у колі |
Рис.6.10 - Шестикутник у квадраті |
При чому, в момент умовного часу t =2,5 елемент сім’ї буде описано відповідним рівнянням
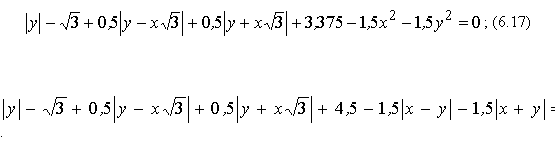 ; (6.17) ; (6.17)
.
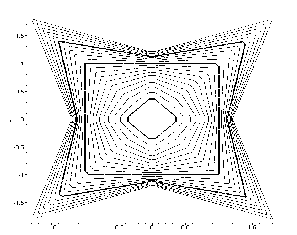
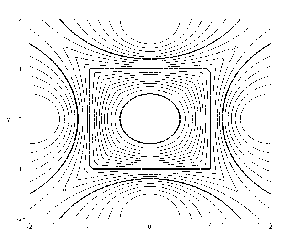
На рис. 6.11 та 6.12 наведено приклади лінійної екстраполяції для варіантів опису вузлових ліній, відповідно:
f1 = 0.4 -½ x½ -½ y½ ; f2 = 2 -½ x - y½ - ½ x + y½ і
f1 =0.25 - x 2 - y 2: f2 = 2 - ½ x - y½ -½ x + y½ : (6.18)
|
|
|
|
Рис.6.11- Ромб в квадраті |
Рис.6.12 - Коло в квадраті |
На рис. 6.13 наведено лінійну екстраполяцію для випадку, коли рівняння початкових зображень мають вид:
f 1 = 1 - ½ x-y ½ - ½ x+y½ ; f2 = f (x -.5, y ) Ú f ( x +.5, y), де f (x, y) = 1- x 2 - y 2.
Рівняння екстрапольованого зображення при t = 2,5 маємо у виді:
 (6.19) (6.19)
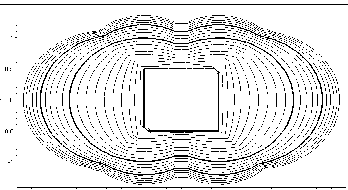
Рис.6.13 - Квадрат у комбінованій області
На завершення наведемо приклади порівняння “трилінійних” поліноміальної та сплайн-екстраполяцій. Для цього використано триточкову Лагранжеву інтерполяційну формулу та формули кубічної сплайн-інтерполяції.
Приклад 1. Нехай рівняння вузлових контурів мають вид:
¨ ромба f 1(x, y) = 0.4 - ½ x½ - ½ y½ :
¨ кола f2(x, y) = 0.5 - x 2 - y 2:
¨ квадрата f 3(x, y) = 2 - ½ x - y½ - ½ x + y½ :
Рівняння “тривузлового” інтерполяційного полінома має вид:
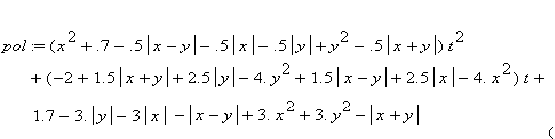 6.20) 6.20)
а рівняння інтерполяційного сплайна – вид:
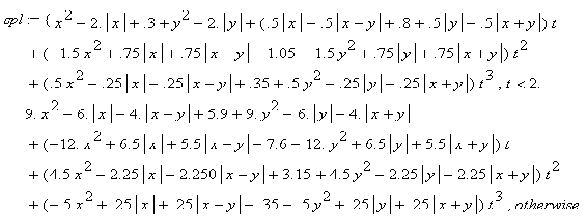
(6.21)
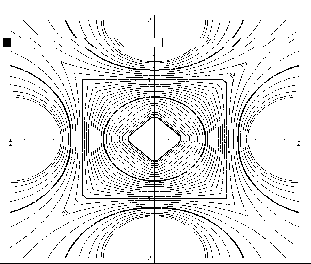
На рис. 6.14 наведено зображення екстраполяційних кривих, побудованих за допомогою формул (6.20) та (6.21). Аналіз зображень доводить переваги сплайн-екстраполяції.
|

|
|
|
Поліноміальна екстраполяція |
Сплайн-екстраполяція |
Рис.6.14 - Варіант трилінійної екстраполяції
з вузловими елементами “ромб - коло - квадрат”
Приклад 2. Нехай рівняння вузлових контурів мають вид:
¨ кола f1 (x, y) º 0.5 - x 2 - y 2 = 0:
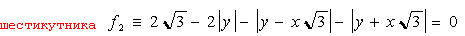
¨ квадрата f 3(x, y) = 3 - ½ x - y½ - ½ x + y½ :
Рівняння “тривузлового” інтерполяційного полінома має вид:
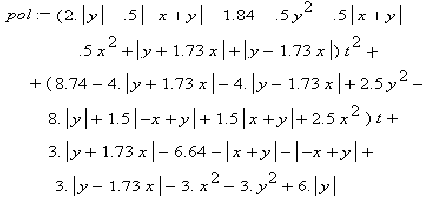 (6.22) (6.22)
а рівняння інтерполяційного сплайна – вид:
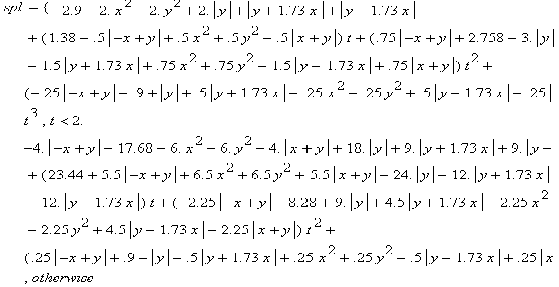 (6.23) (6.23)
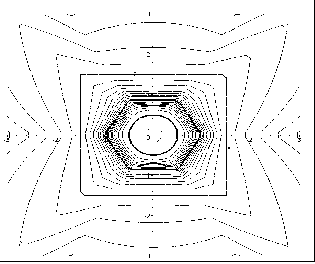
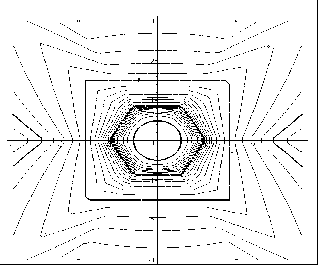
На рис. 6.15 наведено зображення екстраполяційних кривих, побудованих за допомогою формул (6.22) та (6.23). Аналіз зображень також доводить переваги сплайн-екстраполяції.
|
|
|
|
Поліноміальна екстраполяція |
Сплайн-екстраполяція |
Рис. 6.15 - Варіант трилінійної екстраполяції
з вузловими елементами “коло - шестикутник - квадрат”
На рис.6.16 наведено інші варіанти трилінійної екстраполяції.
Рис.6.16 - Приклад трилінійної екстраполяції
|