|
|
Теоретичною основою алгоритму синхронного обертання пари насадок екструдера у вигляді двох трикутників Релло є обкатка трикутника Релло за законом обертового переносу.
Під обертовим переносом на відстань R трикутника Релло Â 1 відносно іншого трикутника Релло Â 2 будемо розуміти переміщення полюса трикутника Â 1 по колу радіуса R з центром в полюсі трикутника Â 2 так, що кожний трикутник сім’ї {Â 1} буде результатом паралельного переносу трикутника Â 2.
Твердження . В результаті обертового переносу трикутника Релло Â 1 на відстань R = a Ö ` 3 буде утворено новий трикутник Â 1.
На рис. 3.5 наведено зображення обертового переносу трикутника Релло в залежності від “дискретності” окремих фаз руху.
Рис. 3.5 - Обертовий перенос трикутника Релло
Твердження. Якщо позначити праву частину рівняння
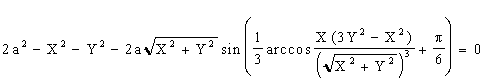 (3.1 (3.1 6)
(що є описом трикутника Релло) як F(X, Y) = 0, то маємо рівняння:
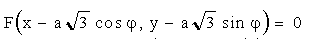 (3.1 (3.1 7)
сім’ї трикутників Релло, підпорядкованих обертовому переносу. Тут j - полярний кут полюса трикутників {Â 1}.
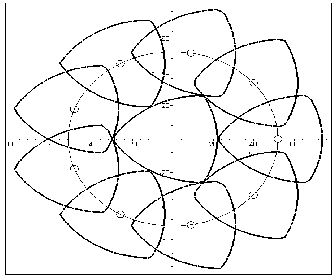
Твердження. При обертовому переносі двох трикутників Релло (4) Â 1 і Â 2 на відстань R = a Ö ` 3 між ними постійно буде здійснюватися постійний точковий дотик (рис. 3.6).
.
|
|
|
|
Рис.3.6 - При обертовому переносі
здійснюється точковий контакт | |
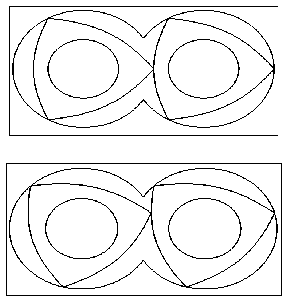
Рис. 3.7 - Синхронне
обер
|
На практиці обертовий перенос дозволяє реалізувати синхронне обертання (тобто в один і той же бік) двох однакових трикутників Релло із забезпеченням між ними постійного точкового контакту.
Позначимо через F(x, y, a ) ліву частину рівняння трикутника Релло (3.15).
Твердження . Опис синхронного обертання двох однакових трикутників Релло із забезпеченням між ними постійного точкового контакту можна здійснити за допомогою виразів:
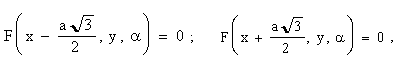 (3.1 (3.1
8)
де значення кута a в цих виразах повинно бути однаковими.
На рис. 3.8 наведено приклади зображення окремих фаз синхронного обертання пари трикутників Релло.
|
> restart:
> with(plots): with(plottools):
> a:=1: # масштабний співмножник
> f := (x,y,alpha) ->
2*a^2-y^2-x^2-2*a*sqrt(x^2+y^2)*cos(Pi/3-
arccos((x^3*cos(3*alpha)+3*y*x^2*sin(3*alpha)-
3*x*y^2*cos(3*alpha)-y^3*sin(3*alpha))/
sqrt(y^6+3*x^2*y^4+3*x^4*y^2+x^6))/3):
> dd:=evalf(a*(1.+sqrt(2)/2.)/2.):
> c1 := circle([-dd,0], 0.5, color=red):
> c2 := circle([dd,0], 0.5, color=red):
> c11 := circle([-dd,0], 0.05,thickness=3 ):
> c22 := circle([dd,0], 0.05,thickness=3 ):
> af := arccos(dd):
> a1 := arc([-dd,0], 1., af..2*Pi-af, color=red):
> a2 := arc([dd,0], 1., Pi-af..-Pi+af, color=red):
> for i from 1 to 12 do
> alpha := i*Pi/20:
> G1 := implicitplot(f(x-dd,y,alpha),x=-2..2,
y=-1..1, scaling=CONSTRAINED,
thickness=3,numpoints=500):
> G2 := implicitplot(f(x+dd,y,alpha),x=-2..2,
y=-1..1, scaling=CONSTRAINED,
thickness=3,numpoints=500):
> G[i] := display({G1,G2},{c1,c2,c11,c22,a1,a2},
axes=BOXED, scaling=CONSTRAINED):
> od:
> plotsetup(gif, plotoutput=`d:rello_0.gif`);
> display(seq(G[i],i=1..12),
insequence=true,scaling=CONSTRAINED); |
Рис. 3.8 - Програма побудови анімаційного зображення
синхронного обертання двох трикутників Релло
Далі наведемо практичне застосування опису трикутника Релло при проектуванні шнекових прес-екструдерів. При цьому, з метою роздрібнення вогнегасного порошку, виникає задача профілювання пари насадок, кожна з яких має форму криволінійного трикутника Релло.
Мається на увазі, що пара насадок обертається синхронно (тобто в один і той же бік). Необхідно скласти алгоритм геометричного моделювання обертання пари трикутників Релло так, щоб в процесі обертання здійснювався точковий дотик. Зазначимо, що саме забезпечення можливого постійного контакту при обертанні запобігає в процесі перетирання налипанню роздрібненої маси на поверхні насадок.
На рис. 3.8 наведено програму мовою Maple V побудови окремих анімаційних фаз обертання пари трикутників Релло, кожний з яких описано за допомогою формули (3.18).
В результаті виконання програми буде утворено файл формату .gif, на якому буде записано анімацію процесу обертання. На рис. 3.9 наведено деякі кадри анімації.
В роботі також запропоновано метод наближеного опису форми трикутника Релло за допомогою рівняння в полярних координатах:
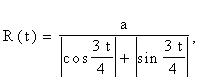 , (3.19) , (3.19)
де t - полярний кут;
а - радіус описаного кола (масштабний співмножник).
До позитивних якостей формули (3.19) слід віднести її простоту. На базі цієї формули можна складати прості алгоритми зображення синхронного обертання двох трикутників Релло. На рис. 3.10 наведено приклад такої програми.
Рис. 3.9 - Синхронне обертання двох трикутників
Релло з кроком 15°
|
> restart: with(plots): with(plottools):
> a:=1: # це масштабний співмножник
> R := a/(abs(cos(3*t/4))+abs(sin(3*t/4))):
> X := R*cos(t): Y := R*sin(t):
> dd:=evalf(a*sqrt(3)/2.):
> c1 := circle([-dd,0], 0.5, color=red):
> c2 := circle([dd,0], 0.5, color=red):
> af := arccos(dd):
> a1 := arc([-dd,0], 1., af..2*Pi-af, color=red):
> a2 := arc([dd,0], 1., Pi-af..-Pi+af, color=red):
> P:=animate([X*cos(u)-Y*sin(u)-dd,X*sin(u)+Y*cos(u),
t=0.01..2*Pi],u=0..2*Pi/3,scaling=CONSTRAINED,
thickness=3,numpoints=200,frames=32,color=black):
> Q:=animate([X*cos(u)-Y*sin(u)+dd,X*sin(u)+Y*cos(u),
t=0.01..2*Pi],u=0..2*Pi/3,scaling=CONSTRAINED,
hickness=3,numpoints=200,frames=32,color=black):
> display([P,Q,c1,c2,a1,a2]); |
Рис. 3.10 - Програма побудови анімаційного зображення
за умови опису трикутників Релло рівнянням (3.19)
Наведені результати можна використати при проектуванні насадок для прес-ектрудерів [11]. При цьому шнековий прес для перетирання вогнегасного порошку повинен складатися з робочої камери, де на двох паралельних валах синхронно обертаються в одному напрямку шнеки й групи насадок-роздрібнювачів. Активний профіль кромки насадки-роздрібнювача має форму трикутника Релло.
Процес перетирання вимагає, щоб пара насадок, які розташовані в одній площині, була установлена з можливістю постійного контакту при обертанні. Це запобігає в процесі перетирання налипанню роздрібненої маси на поверхні насадок.
Тому вважатимемо розв’язаною задачу пошуку такої геометричної форми профілю насадок-роздрібнювачів, яка б задовольняла вимогам постійного точкового дотику під час синхронного обертання валів шнекового прес-екструдера. В роботі показано, що цим вимогам задовольняють насадки у формі трикутників Релло. При цьому реалізується “паралельна” обкатка трикутника Релло за схемою обертового переносу.
|