|
|
Для того, щоб правильно оцінити енергетичні параметри направленого вибуху, необхідно побудувати сім’ю “вибухових” променів, які відбито синусоїдальним екраном. При цьому мається на увазі, що кожний з променів “несе на собі” частку вибухової енергії. Тому для досліджень певний інтерес представляє наочне зображення сім’ї променів (кінці яких є складовими фронтів вибухових хвиль), що утворилися в результаті відбиття від синусоїдальної поверхні сім’ї паралельного або центрального пучка променів.
Для пояснення запропонованого методу складання рівнянь спочатку розглянемо випадок на площині.
Нехай в декартовій прямокутній системі координат Oxy маємо рівняння 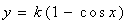 “дзеркальної” кривої. Джерело променів розташуємо в точці з координатами S(x0, y0). Точку падіння променя на криву позначимо М(x, “дзеркальної” кривої. Джерело променів розташуємо в точці з координатами S(x0, y0). Точку падіння променя на криву позначимо М(x, 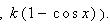 ). В точці падіння вектор нормалі матиме координати ). В точці падіння вектор нормалі матиме координати 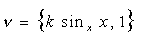 . Тут k sinxx є значенням похідної функції . Тут k sinxx є значенням похідної функції 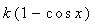 в точці x. Опис відбитого променя базується на такому твердженні. в точці x. Опис відбитого променя базується на такому твердженні.
Твердження. Точки S(x0, y0) і К(x2, y2) будуть розташовані симетрично відносно прямої 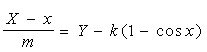 (що є нормаллю до кривої у точці М) тоді, коли будуть виконуватися співвідношення: (що є нормаллю до кривої у точці М) тоді, коли будуть виконуватися співвідношення:
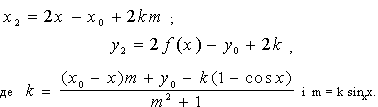
, (7.8)
Отже, координати відбитого променя можна обчислити за формулами {x2 - x, y2 - y}, а вирази для обчислення координат будь-якої точки на відбитому промені (в залежності від t) мають вид:
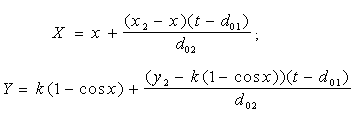 . (7.9) . (7.9)
Тут t - величина, яка характеризує “час розповсюдження” фронту хвилі.

У формулах (7.9) враховано шлях, що проходить кожний з променів до точки відбиття.
На рис. 7.11 наведено текст Maple- програми побудови сім’ї променів, які відбито синусоїдою 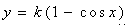 за умови, що джерело променів має координати (0, k). за умови, що джерело променів має координати (0, k).
|
> restart: with(plots): with(plottools):
> a := -Pi/2: b := Pi/2: c := 0: d := Pi:
> xs := 0: N := 12:
> f := x -> (1.- cos(x))*0.7072: ys := f(Pi/2):
> df := unapply(D(f)(x),x):
> G := plot(f(x), x=a..b, thickness=3):
> S := circle([xs,ys], 0.05,thickness=3):
> Ot := seq( line( [1.5*i/N, f(1.5*i/N)],
[(1.5*i/N) + (d - f(1.5*i/N))/
( ( 2*df( 1.5*i/N )*( xs - 1.5*i/N ) +
( ys - f(1.5*i/N))*
( df(1.5*i/N)^2 -1.) ) /
( 2*df(1.5*i/N)*(ys - f(1.5*i/N))-
( xs - 1.5*i/N)*( df(1.5*i/N)^2 -1.))),d]),i=-N..N):
> paral[k] := evalf(add( arctan(
abs((1.5*i/N) + (d - f(1.5*i/N))/
( ( 2*df( 1.5*i/N )*( xs - 1.5*i/N ) +
( ys - f(1.5*i/N))*( df(1.5*i/N)^2 -1) ) /
( 2*df(1.5*i/N)*(ys - f(1.5*i/N))-
( xs - 1.5*i/N)*( df(1.5*i/N)^2 -1) ))-1.5*i/N)/
abs(f(1.5*i/N)-d)), i=0..2*N/3)):
> Pic := display({S,G,Ot},
axes=normal, scaling=constrained, view=c..d):
> display(Pic, axes=normal,
scaling=constrained, view=[a..b,c..d]); |
Рисунок 7.11 - Програма побудови сім’ї променів, відбитих від синусоїди 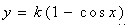 за умови, що її квазифокус розташовано на рівні кінців фрагмента на проміжку [ -p /2, p /2]. за умови, що її квазифокус розташовано на рівні кінців фрагмента на проміжку [ -p /2, p /2].
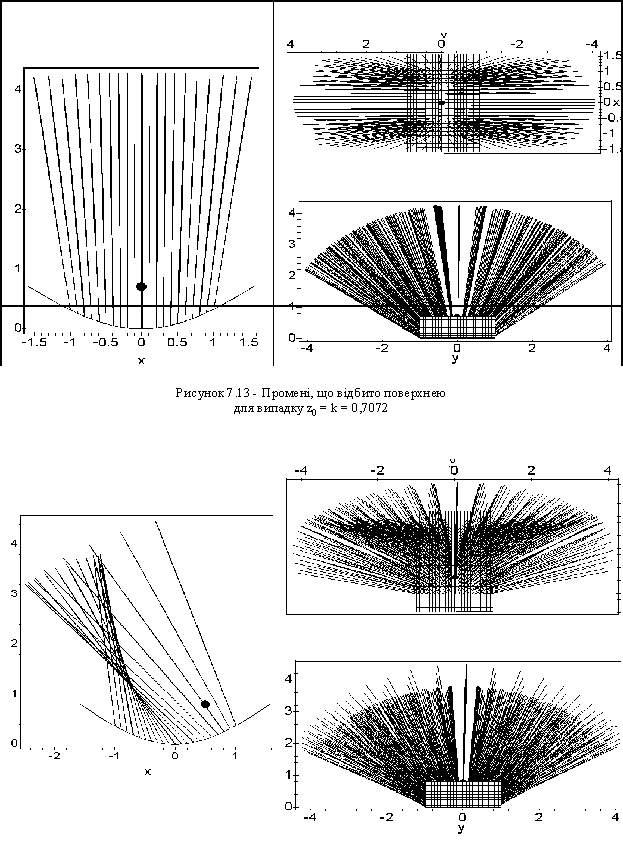
На рис. 7.12 зображено результати роботи програми трасування променів для випадку k = 0,7072. Складена програма дозволяє шляхом проведення машинних експериментів відшукати таке значення k, щоб виконувалася умова функціонування відбивальної системи. Тобто можна показати, що коли джерело променів розмістити в точці з координатами (0; 0,7072) (в підрозділі 2.3 ця точка названа квазифокусом), то відбиті синусоїдою y = 0,7072 (1 - cos x) промені будуть спрямовані “майже паралельно” вздовж осі Oy.
Причому точка джерела променів буде розташована на одному рівні з кінцями фрагмента синусоїди на проміжку [ -p /2, p /2]. Саме це головне для даної роботи положення проілюстровано на рис. 7.12.
Для наочності розглянемо просторовий випадок відбиття променів і розв’яжемо задачу опису та зображення променів ударних хвиль, відбитих від циліндричної синусоїдальної поверхні. В даному випадку промені утворені в результаті відбиття іншого пучка променів, джерело яких розташовано в заданій точці простору.
Нехай в декартовій системі координат Oxyz профіль циліндричної поверхні описано рівнянням z = k(1 - cos x). Джерело вибуху розташуємо в точці з координатами S(x0 ,y0, z0).
Вважається, що відбитий від поверхні L будь - який промінь не матиме з нею інших спільних точок (тобто відбиття променів від поверхні відбувається лише один раз).
Точку падіння променя на циліндричну синусоїдальну поверхню позначимо як P(x1 ,y1, z1). В точці падіння вектор нормалі поверхні матиме координати 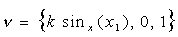 . Тут k sinx(x1) є значенням похідної функції k(1 - cos x) в точці x1. . Тут k sinx(x1) є значенням похідної функції k(1 - cos x) в точці x1.
Алгоритм побудови променя, який відбито поверхнею, базується на наступному твердженні.
Твердження. Точки S(x0 ,y0, z0) і M(x2 ,y2, z2) розташовані симетрично відносно прямої L: 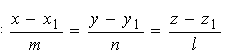 тоді, коли будуть виконуватися співвідношення: тоді, коли будуть виконуватися співвідношення:
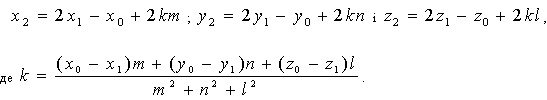
Зазначимо, що координати відбитого променя можна обчислити за формулами {x2 - x1, y2 - y1, z2 - z1}.
Звідси маємо ще одне твердження.
Твердження. Вирази для обчислення координат вектора відбитого від синусоїдального циліндра променя мають вид:
коли будуть виконуватися співвідношення:
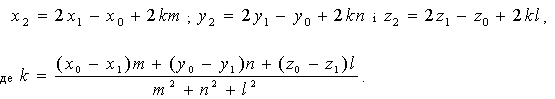
Зазначимо, що координати відбитого променя можна обчислити за формулами {x2 - x1, y2 - y1, z2 - z1}.
Твердження . Вирази для обчислення координат вектора відбитого від синусоїдального циліндра променя мають вид:
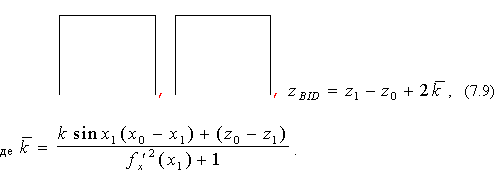
Враховуючи попереднє твердження, визначимо координати одиничного вектора відбитого променя:
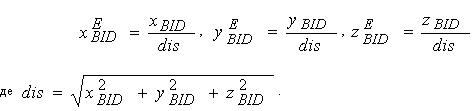
Координати будь-якої точки на відбитому промені можна обчислити за формулами:
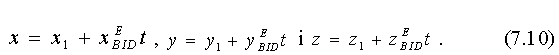
Тут t - величина, яка характеризує час розповсюдження хвилі вибуху.
Одержані співвідношення покладено в основу програми побудови відбитих променів, яка написана мовою Maple V (рис. 7.12). В результаті її виконання буде сформовано два масиви з координатами початку (W) і кінця (Q) кожного з елементів сім’ї відбитих від поверхні променів. Поверхнею є синусоїдальний циліндр, профіль якого описано синусоїдою 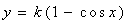 за умови, що джерело променів має координати (x0, y0, z0). за умови, що джерело променів має координати (x0, y0, z0).
На основі програми можна проводити “наочні” дослідження впливу на відбивальні властивості синусоїдальної циліндричної поверхні як величини пружного згину металевого листа (характеризується параметром p), так і місця розташування “точкового” джерела вибуху (характеризується координатами точки S).
|
> restart: with(plots): with(plottools):
> f := x -> k*(1.-cos(x)): df := unapply(D(f)(x),x):
> x0 := 0.: y0 := 0.: z0 := 0.7072: k := 0.7072:
> gelob := plot3d(f(x,y), x=-Pi/2..Pi/2, y=-1..1):
> zaryd := sphere([x0,y0,z0], 0.07): q := 0:
> for j from -10 to 10 do for i from -10 to 10 do
> x1 := evalf(i*0.1)+0.01; y1 := evalf(j*0.1)+0.01:
> z1 := evalf(f(x1));
> m := - df(x1); n := 0.: l := 1.;
> g := ((x0-x1)*m+(y0-y1)*n+(z0-z1)*l)/(m^2+n^2+l^2):
> x2 := 2.*x1 - x0 + 2.*m*g;
> y2 := 2.*y1 - y0 + 2.*n*g;
> z2 := 2.*z1 - z0 + 2.*l*g;
> aotr := x2 - x1; botr := y2 - y1; cotr := z2 - z1;
> d02:=sqrt(aotr^2+botr^2+cotr^2):
> xEd:=aotr/d02; yEd:=botr/d02; zEd:=cotr/d02;
> d01:=sqrt((x0-x1)^2+(y0-y1)^2+(z0-z1)^2):
> t:=5.:
> X:=x1+(t-d01)*xEd; Y:=y1+(t-d01)*yEd;
> Z:=z1+(t-d01)*zEd; q := q+1:
> W[q,1]:=x1; W[q,2]:=y1; W[q,3]:=z1;
> Q[q,1]:=X; Q[q,2]:=Y; Q[q,3]:=Z;
> od; od;
> G := seq( line( [ W[q,1],W[q,2],W[q,3] ],
[ Q[q,1],Q[q,2],Q[q,3] ] ), q=1..420 ):
> display(G,gelob,zaryd, orientation=[-125,55],
scaling=CONSTRAINED,axes=boxed); |
Рисунок 7.12 - Програма побудови променів, відбитих від
циліндричної синусоїдальної поверхні
|
Рисунок 7.14 - Промені, що відбито поверхнею для випадку z0=k=0,8 i x=0,5 |
ною для аналізу енергетичних характеристик вибуху. В подальшому викладі для наочного представлення наслідків вибуху буде розглянуто поняття фронту ударної хвилі.

Рисунок 7.15 - Промені, що відбито поверхнею для випадку
z0 = k = 0,7072 (а) i z0 = k = 0,6 (б)
|
|
|