|
|
Вище зазначалося, що наочно сплайн-функцію можна представити у вигляді гнучкої сталевої лінійки, закріпленої у вузлових точках, що плавно згинається. Завдяки зазначеним властивостям сплайнів, вони непогано описують як функції, представлені невеликим числом вузлових точок (завдяки плавності сплайн-кривих), так і функції, що представляються дуже великим числом вузлових точок (оскільки порядок поліномів від цього числа вже не залежить).
Недоліком сплайн-інтерполяції є відсутність загального виразу для всієї кривої. Фактично доводиться використовувати набір сплайн-функцій для різних інтервалів між вузловими точками.
Для одержання сплайн-інтерполяції використовується Maple-функція spline (X, Y, var, d). Тут X і Y — одномірні вектори однакового розміру, що визначають значення вихідної функції у координатах вузлових точок (причому у довільному порядку); var — ім'я перемінної, відносно якої обчислюється сплайн-функція, нарешті, необов'язковий параметр d задає вид сплайну. Він може мати наступні значення: linear - лінійна функція, поліном першого порядку quadratic — квадратична функція, поліном другого порядку; cubic - поліном третього порядку; quartic — поліном четвертого порядку. Якщо параметр d опущений, то сплайн-функція буде будуватися на основі поліномів третього порядку (кубічні сплайни).
Техніку сплайновой інтерполяції пояснює програма, наведена на рис. 2.3. На ньому представлене завдання векторів вузлових точок X і Y і чотирьох сплайнових функцій, за якими побудовані їхні графіки. Для сплайн-функцій показані також отримані аналітичні вирази.
Як видно з рис. 2.3, сплайнова функція являє собою кускову функцію, визначену на окремих інтервалах. При цьому на кожній ділянці така функція описується окремим поліномом відповідного ступеня. Функція plot “розуміє” такі функції і дозволяє без перетворення типів даних будувати їхні графіки. На рис. 2.4 наведено результат роботи розглянутої програми.
Зазначимо, що для роботи з кусковими функціями також можна використовувати функції convert і piecewise.
restart:
readlib(spline):X := 'X': Y := 'Y':
X := [0, 1, 2, 3, 4, 5]:
Y := [0, 1, 4, 3, 2, 1]:
fl := spline (X,Y,x,linear);
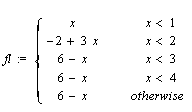
fq := spline(X,Y,x,quadratic);
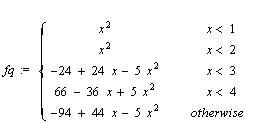
fc := spline(X,Y,x,cubic);
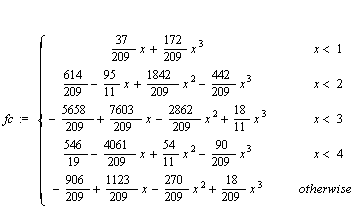
fql := spline(X,Y,x,quartic);
plot([fl,fc,fq,fql], x=-1..6, у=-1..5, color=black);
Рис. 2.3 - Програма побудови сплайн-функції
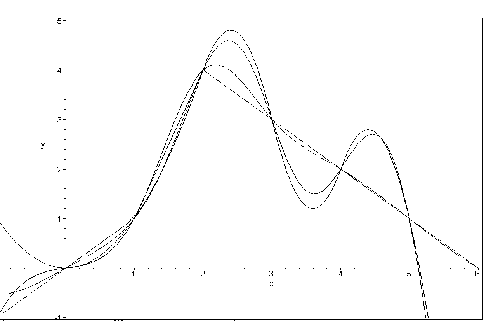
Рис. 2.4 - Приклад зображення чотирьох сплайн-функцій
Перейдемо до складання програми зображення області розпорошення вогнегасного матеріалу із пожежного ствола. Для цього визначимо сплайн за значеннями радіус-векторів (тут r - змінна величина - параметр анімації):
Y:=[0,0.2*r,1*r,5*r,10*r,12*r,10*r,5*r,1*r,0.2*r,0]:
у вузлових “точках” (тобто для значень полярних кутів):
X:=[0, Pi/10, 2*Pi/10, 3*Pi/10, 4*Pi/10,
5*Pi/10,6*Pi/10, 7*Pi/10, 8*Pi/10, 9*Pi/10, Pi]:
На рис. 2.5 наведено програму побудови анімаційного зображення процесу розпорошення вогнегасної речовини. В результаті виконання програми на диску с буде сформовано файл stvol.gif, який буде містити анімаційні кадри динамічної сцени розповсюдження вогнегасної речовини, яка надходить з пожежного ствола.
Приклади анімаційних кадрів наведено на рис. 2.6. На рис. 2.7 наведено суміщені фронти розпорошення (повернуто на 90° ).
|
restart: with(plots): with(plottools):
XX:=[0, Pi/10, 2*Pi/10, 3*Pi/10, 4*Pi/10,
5*Pi/10,6*Pi/10, 7*Pi/10, 8*Pi/10, 9*Pi/10, Pi]:
Ll := line([0.5,-3], [0.5,0],thickness=3,
scaling=CONSTRAINED):
L2 := line([-0.5,-3], [-0.5,0],thickness=3,
scaling=CONSTRAINED):
L3 := line([-0.5,-3], [0.5,-3],thickness=3,
scaling=CONSTRAINED):
for i from 1 to 50 do
r := evalf(i/25):
YY:=[0,0.2*r,1*r,5*r,10*r,12*r,10*r,5*r,1*r,0.2*r, 0]:
R := evalf(spline(XX,YY,t,cubic)):
bax := plot([R,t,t=0..Pi],coords=polar,
scaling=CONSTRAINED, thickness=3, axes=BOXED):
Gr[i] := display(Ll,L2,L3, bax,view = [-8..8,-3..25]):
end do:
display(seq(Gr[i],i=1..50),scaling=CONSTRAINED ,
insequence=true);
for i from 1 by 5 while i < 50 do Gr[i]; od;
plotsetup(gif, plotoutput= `c:stvol.gif`);
display(seq(Gr[i],i=1..50), scaling=CONSTRAINED,
insequence=true);
|
Рис. 2.5 - Програма побудови анімаційного зображення
процесу розпорошення вогнегасної речовини
Рис.2.6 - Приклади анімаційних кадрів
розпорошення вогнегасної речовини
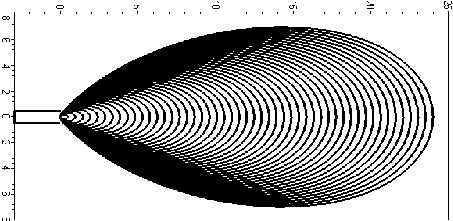
Рис. 2.7 - Суміщені фронти розпорошення вогнегасної речовини
(повернуто на 90° )
На рис. 2.8 наведено модифікацію цієї програми, де фронти розпорошення розповсюджуються по діагоналі екрану (іноді це є більш зручним). На рис. 2.9 та 2.10 наведено приклади виконання програми.
|
XX:=[0, Pi/20, 2*Pi/20, 3*Pi/20, 4*Pi/20, 5*Pi/20,
6*Pi/20, 7*Pi/20, 8*Pi/20, 9*Pi/20, Pi]:
Ll := line([-3,3], [3,-3], color=red, linestyle=3):
for i from 1 to 50 do
r := evalf(i/25):
YY:=[0,0.2*r,1*r,5*r,10*r,12*r,10*r,5*r,1*r,0.2*r, 0]:
R := evalf(spline(XX,YY,t,cubic)):
bax := plot([R,t,t=0..Pi],coords=polar,
scaling=CONSTRAINED, thickness=3, axes=NONE):
Gr[i] := display(Ll, bax):
end do:
display(seq(Gr[i],i=1..50),scaling=CONSTRAINED,
insequence=true);
for i from 1 by 5 while i < 50 do Gr[i]; od;
plotsetup(gif, plotoutput= `c:stvol_2.gif`);
display(seq(Gr[i],i=1..50), scaling=CONSTRAINED,
insequence=true); |
Рис. 2.8 - Програма побудови анімаційного зображення
процесу розпорошення вогнегасної речовини (другий варіант)
Рис. 2.9 - Анімаційні кадри розпорошення вогнегасної речовини
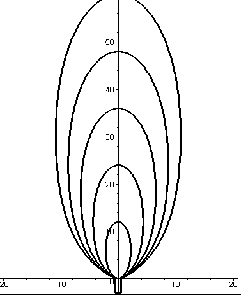
Рис. 2.10 - Суміщені фази розпорошення вогнегасної речовини
На практиці зручно використовувати більш просту програму, яка зображена на рис. 2.11. Ця програма дозволяє будувати як окремі, так і суміщені зображення фронтів зон розпорошення вогнегасної речовини. Тут для полярного кута обрано наступну дискретизацію:
{ 0; p /10; 2p /10; 3p /10; 4p /10; 5p /10; 6p /10; 7p /10; 8p /10; 9p /10; p }.
|
restart: with(plots): with(plottools):
XX:=[0, Pi/10, 2*Pi/10, 3*Pi/10, 4*Pi/10,
5*Pi/10,6*Pi/10, 7*Pi/10, 8*Pi/10, 9*Pi/10, Pi]:
Ll := line([0.5,-3], [0.5,0],thickness=3,
scaling=CONSTRAINED):
L2 := line([-0.5,-3], [-0.5,0],thickness=3,
scaling=CONSTRAINED):
L3 := line([-0.5,-3], [0.5,-3],thickness=3,
scaling=CONSTRAINED):
for i from 1 to 5 do
YY:=[0,0.2*i,1*i,5*i,10*i,12*i,10*i,5*i,1*i,0.2*i, 0]:
YY:=[0,0.5*i,2*i,7*i,11*i,12*i,11*i,7*i,2*i,0.5*i, 0]:
YY:=[0,1*i,3*i,7*i,11*i,12*i,11*i,7*i,3*i,0.1*i, 0]:
YY:=[0,0.1*i,1*i,3*i,7*i,12*i,7*i,3*i,1*i,0.1*i, 0]:
R := evalf(spline(XX,YY,t,cubic)):
bax := plot([R,t,t=0..Pi],coords=polar,
scaling=CONSTRAINED, thickness=3, axes=BOXED):
Gr[i] := display(Ll,L2,L3,bax,view=[-23..23,-3..61]):
end do:
display(seq(Gr[i],i=1..5),scaling=CONSTRAINED);
for i from 1 to 5 do Gr[i]; od; |
Рис. 2.11 - Програма побудови окремих та суміщених зображень фронтів зон розпорошення вогнегасної речовини
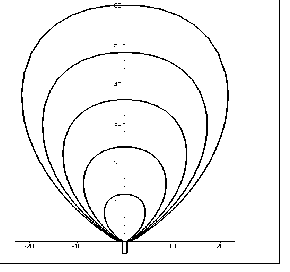
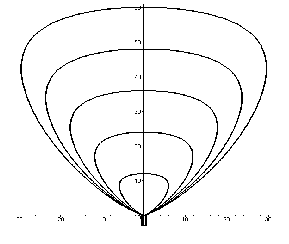
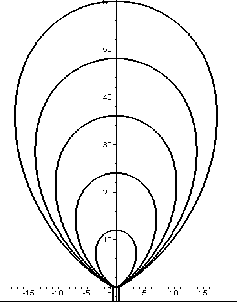
В залежності від обраного вектора з координатами значень радіус-векторів, маємо варіанти геометричних форм зон розпорошення. На рис. 2.12 - 2.1 5 зображено відповідні варіанти для значень радіус – векторів.
{0, 0.5*i, 2*i, 7*i, 11*i, 12*i, 11*i, 7*i, 2*i, 0.5*i, 0}
{ 0, 0.1*i, 3*i, 10*i, 12*i, 12*i, 12*i, 10*i, 3*i, 0.1*i, 0}:
{ 0, 0.1*i, 1*i, 3*i, 7*i, 12*i, 7*i, 3*i, 1*i, 0.1*i, 0}:
{ 0, 0.2*i, 1*i, 5*i, 10*i, 12*i, 10*i, 5*i, 1*i, 0.2*i, 0}:
|
|
|
|
Рис. 2.12 |
Рис. 2.13 |
|
|

|
|
Рис. 2.14 |
Рис. 2.15 |
|
|
|