|
|
При розв’язанні задач оптики застосовується метод оберненого променя. Суть його полягає ось в чому. Якщо промінь виходить з точки А і після відбиття від поверхні П потрапляє в точку В, то, виходячи з точки В і здійснивши обернений шлях, промінь потрапить в точку А.
Тобто (теоретично) точки джерела і приймача променів при розрахунках можна міняти місцями. Наочно це можна спостерігати на прикладі супутникових параболічних антен: антени передавача і приймача мають ідентичну конструкцію.
Для реалізації методу оберненого променя на практиці необхідно у відбивальній системі виявити точки, які підпорядковані закону двоїстості. В даній роботі пропонується варіант розв’язання цієї задачі.
В результаті застосування алгоритму трасування променів, відбитих від кривої, на рис. 7.5 наведено приклади відповідних зображень, де можна спостерігати один з об’єктів дослідження прикладної геометрії - обвідну сім’ї відбитих променів. Цей геометричний об’єкт ще називають катакаустикою кривої.
Легко помітити, що катакаустика, як обвідна сім’ї відбитих променів, звичайно має форму “дзьобу” з точкою загострення, яка називається точкою повернення або особливою точкою . Це має місце для достатньо широкого класу гладких кривих, які є “опуклими від точки” джерела променів.
Далі покажемо, що між точкою джерела променів та точкою повернення катакаустики існує залежність двоїстості.
Твердження. Якщо А є точкою джерела променів, а В - точкою повернення катакаустики, то точки А і В задовольняють властивостям двоїстості - тобто якщо точка В є джерелом променів, то А буде точкою повернення катакаустики.
Для визначення координат точки повернення катакаустики розглянемо опис обвідної сім’ї променів, відбитих від гладкої кривої. Для цього використаємо опис сім’ї відбитих променів, рівняння якої позначимо як Ф(x, y, z) = 0.
Катакаустикою відбивальної кривої y = f(x) буде обвідна сім’ї відбитих прямих, для знаходження рівняння якої необхідно вилучити параметр z з системи нелінійних рівнянь:
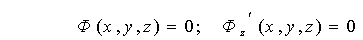 . (7.4) . (7.4)
На рис. 7.4 наведено Maple-програму аналітичного опису та побудови катакаустики для випадку, коли кривою є синусоїда y = k (1 - cos x), а джерелом променів є точка S(xS, yS).
|
> restart: with(plots): with(plottools):
> xs:=0.: ys:=5000.: k:=0.8:
> f := z -> (1.- cos(z))*k: df:=diff(f(z),z):
> mm:=z-xs: nn:=f(z)-ys:
> m:=mm/sqrt(mm^2+nn^2): n:=nn/sqrt(mm^2+nn^2):
> F:=(y-f(z))* ( 1.+2.*df / (1.-df^2) *(n/m) ) -
(x-z)*( (2.*df/(1.-df^2) )-n/m): Fz:=diff(F,z):
> FF:=solve({F=0,Fz=0}, {x,y}): assign(FF): x,y:
> z:=0.001: y_fok:=evalf(10000*y); unassign('z'):
> Q:=plot([x,y, z=-Pi/2..Pi/2],thickness=2):
> W:=plot(f(z), z=-Pi/2..Pi/2,thickness=4):
> display([Q,W], view=0..Pi/2,scaling=CONSTRAINED);
|
Рисунок 7.4 - Maple-програма опису та побудови катакаустики
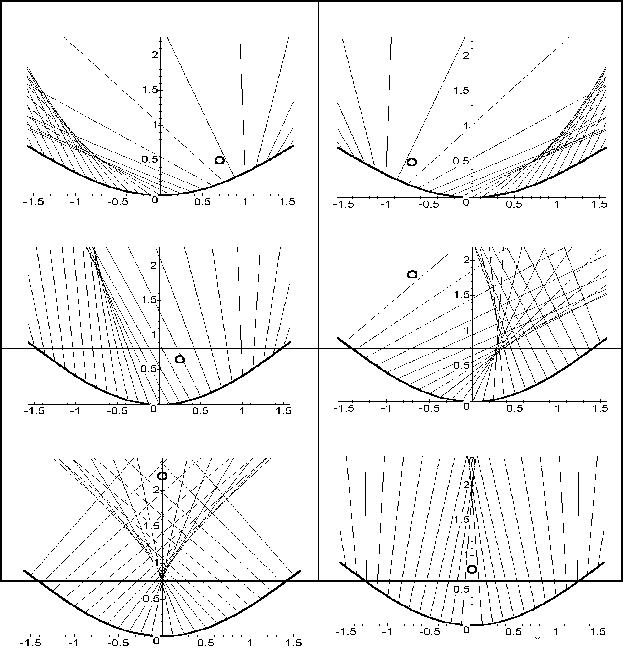
На рис. 7.5 також зображено приклади двоїстих точок джерела променів і точок повернення катакаустики. Розглянуто варіанти розташування точок:
A(0,7; 0,5); B(-0,7; 0,5) і синусоїди y = 0,7072 (1 - cos x) (верхній рисунок),
A(-0,7; 1,8); B(0,25; 0,65) і синусоїди y = 0,9 (1 - cos x) (середній рисунок) та А(0; 2,2); B(0; 0,8) і синусоїди y = 0,9 (1 - cos x) (нижній рисунок).
|
|
|
|
|
|
|
|
|
Рисунок 7.5 - Приклади двоїстих точок джерела і точок повернення
Розглянуту двоїстість між точкою джерела променів та точкою повернення катакаустики в даній роботі покладено в основу методу оберненого променя. При цьому мається на увазі, що одна з двоїстих точок буде розташована “безмежно далеко”, тобто буде невласною.
Визначення. Квазифокусом кривої будемо називати точку повернення обвідної сім’ї відбитих від цієї кривої променів за умови, що на обрану криву падає множина паралельних променів - тобто джерелом променів є невласна точка.
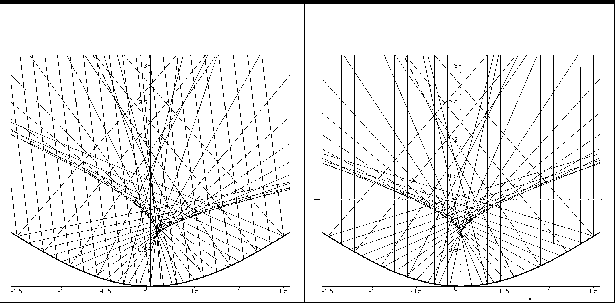
На рис. 7.6 наведено катакаустики в залежності від кута падіння з невласної точки сім’ї паралельних променів на синусоїду y = 0.7(1 - cos x). Тут і далі мається на увазі, що на криву промені падають “зверху вниз”.
Згідно з положенням методу оберненого променя, доцільно припустити, що коли джерело променів розташувати в квазифокусі синусоїди, то відбиті промені мають пройти через невласну точку. Далі будемо вважати, що відбиті промені матимуть напрям “паралельно” осі Oy.
|
|
|
Рисунок 7.6 - Катакаустики синусоїди в залежності
від кута падіння множини паралельних променів
з невласної точки
На рис. 7.7 для порівняння зображено катакаустику параболи y = 0.5(x2 - 1), де падаючі промені утворюють з віссю Oy кут a . Зазначимо, що коли a = 0, то катакаустика вироджується у точку - фокус параболи.
Рисунок 7.5 - Приклад катакаустик для параболи
Для впроваджень при складанні програм необхідно мати аналітичні описи катакаустики. У випадку, коли крива задана в загальному виді y = f (x) і коли падаючі промені спрямовані вздовж вектора {m, n} опис катакаустики має вид:
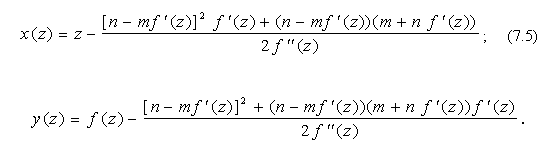
На рис. 7.8 наведено Maple- програму, яка дозволяє в аналітичному виді знаходити опис катакаустики кривих для невласного джерела променів. На аналітичному рівні засобами математичного процесора Maple V здійснюється розв’язання системи нелінійних рівнянь (7.5). При цьому для контролю будуються зображення кривої та її катакаустики.
|
> restart: with(plots): with(plottools):
> p:=1.: alpha:=0.0000001: rrr:=evalf(alpha*Pi/180.):
> m:=evalf(sin(rrr)): n:=evalf(cos(rrr)): tgb:=n/m:
> f := z -> p*(1 - cos(z)): df:=diff(f(z),z):
> G := line([10*m,10*n],[0,0], thickness=1):
> tg_2a := 2*df / (1-df^2):
> tg_gam := (tg_2a-tgb)/(1+tg_2a*tgb):
> F := y-f(z)-(x-z)*tg_gam:
> Fz := diff(F,z):
> FF := solve({F=0,Fz=0},{x,y}):
> assign(FF): x,y:
> Q := plot([x,y, z=-Pi/2..Pi/2],thickness=2):
> W := plot(f(z), z=-Pi/2..Pi/2,color=0,thickness=4):
> display([Q,W,G], view=0..1.5,scaling=CONSTRAINED):
> x := evalf(combine(x),5); y := evalf(combine(y),5);
> QQ := plot([x,y, z=-Pi/2..Pi/2],thickness=2):
> display([QQ,W,G], view=0..2,scaling=CONSTRAINED); |
Здійснюється перевірка знайденого аналітичного розв’язання
|
> alpha:=rrr:
> xP:= (-.625*z+.125*z*cos(4*z)-.5*z*cos(2*z)
-.125*sin(4*z)+.75*sin(2*z))/
(-.625-.5*cos(2*z)+.125*cos(4*z));
> yP:=(.4375*cos(z)+.09375*cos(3*z)-.031251*cos(5.*z)-
.62500+.125*cos(4*z)-.5*cos(2*z))/
(-.625-.5*cos(2*z)+.125*cos(4.*z));
> QQ:=plot([xP,yP, z=-3..3],thickness=2):
> display([QQ,W,G], view=0..1.5,scaling=CONSTRAINED); |
Рисунок 7.8 - Програма опису в аналітичному виді
катакаустики кривих
Складена програма дозволяє одержати нові результати, які ми представимо як твердження.
Твердження. Якщо на синусоїду y = 1 - cos x падають паралельні промені, напрям яких є оберненим до напряму осі Oy, то рівняння катакаустики має вид:

Твердження. Якщо на синусоїду y = p(1 - cos x) падають паралельні промені назустріч напряму осі Oy, то рівняння катакаустики має вид:
;

Підставивши у формули (7.7) значення z = 0, маємо x0 = 0; y0 = 0,5 / p. Наслідком цього є наступне твердження, яке ми будемо використовувати при розрахунку циліндричних синусоїдальних відбивачів.
Твердження. Квазифокус синусоїди y = p(1 - cos x) має координати K(0; 0,5/p) за умови, що на синусоїду паралельні промені падають назустріч напряму осі Oy.
Ілюстрацію “оптичних” властивостей синусоїди наведено на рис. 7.9 та рис. 7.10, де джерело променів розташовано в квазифокусі синусоїди.
Рисунок 7.9 - Приклади відбиття променів синусоїдою
y = p (1 - cos x)
для параметрів p=0,25 (a); p=0,5 (б); p=0,75 (в) i p=1 (г)
за умови, що джерело розташовано в квазифокусі
Рисунок 7.10 - Приклади відбиття променів синусоїдою
y = p (1 - cos x)
для параметрів p=1,5 (a); p=2,5 (б); p=5 (в) i p=10 (г)
за умови, що джерело розташовано в квазифокусі
|