|
У попередніх пунктах показано, як за допомогою виразів x = x(a ) i y = y(a ) описати RP-проекції осьового перетину факела. При цьому обчислення локальних ККВ для різних x = p здійснено за формулою:
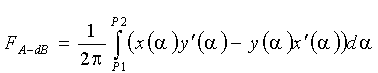 . (5.27) . (5.27)
Після обчислень одержимо значення локального ККВ у довільній точці А. Це значення як довжину відрізка АВ відкладемо з точки А вздовж осі Oz. У результаті одержимо графік Г розподілу значень локальних ККВ на осі Ох (рис. 5.24).
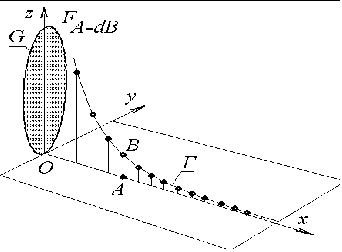
Рис. 5.24 - Графік значень локальних ККВ
Враховуючи, що фігура G є осьовим перетином поверхні обертання, дійдемо висновку, що графік розподілу локальних ККВ буде поверхнею обертання, співвісною з факелом

(рис. 5.25).
Рис. 5.25 - Розподіл локальних ККВ
У роботі вважається, що інтегральний ККВ для фігури G на площині Оху можна оцінити об’ємом тіла, обмеженого площиною Оху, графіком розподілу локальних ККВ та горизонтально – проеціюючою циліндричною поверхнею, у якої напрямна збігається із контуром фігури G. На рис. 5.26 наведено схему дискретизації графіка.
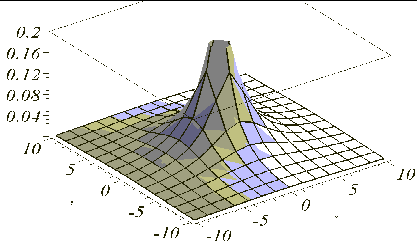
Рис. 5.26 - Дискретизація графіка
На рис. 5.27 наведено відсік поверхні у випадку інтегрування по прямокутнику.
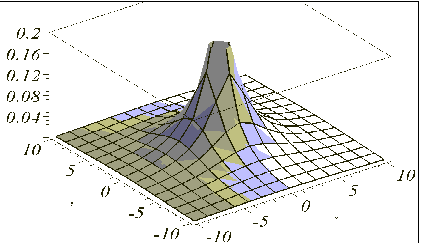
Рис. 5.27 - Елементарний відсік об’єму
У результаті маємо формулу для обчислення інтегральних ККВ у виді:
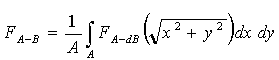 . (5.25) . (5.25)
|