|
|
Вважається, що багатокутником здійснено апроксимацію контура (або контурів) даного зображення. Подальша мета - описати апроксимаційний багатокутник рівнянням у неявному виді F(x, y) = 0. Причому громіздкість аналітичного виразу не вплине на його застосування, адже реалізацію буде здійснено на сучасній ЕОМ.
Нехай у декартовій системі координат Oxyz на площині z = 0 задана крива лінія ¶ G0, що обмежує фігуру G0 кінцевих розмірів і складається з відрізків прямих ліній. Наведемо розроблену Maple - програму опису багатокутника у виді нормального рівняння F(x, y) = 0, яка базується на відомому алгоритмі В.Л.Рвачова визначення багатокутника за допомогою R-функцій.
Спочатку вводиться поняття простого багатокутника, що обмежує на площині деяку фігуру W. При цьому вхідними даними служать координати вершин (x1,y1), (x2,y2), ..., (xn,yn) і інформація про западини багатокутника. Визначення. Багатокутник називається простим, якщо: 1) з кожної його вершини виходять тільки дві сторони; 2) сторони не мають спільних точок; 3) вершини не лежать на його сторонах.
Доповнимо простий багатокутник до опуклого. Нехай цей опуклий багатокутник обмежує на площині деяку фігуру V. Різниця множин V W утворить западини простого багатокутника.
Визначення. Орієнтованим нормальним рівнянням прямої, що проходить через точки (x1,y1) і (x2,y2), називається вираз виду:
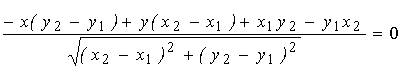 . (6.1) . (6.1)
При цьому функція, що у лівій частині рівняння (6.1) (позначати її будемо так F1(x,y) ), задовольняє властивості: якщо рухатися відрізком від точки (x1,y1) до точки (x2,y2), то для точок площини, розташованих ліворуч, завжди буде виконуватися нерівність F1(x,y) > 0, а для точок, розташованих праворуч, - нерівність F(x,y)1 < 0. Крім того, значення функції F1(xА, yА) в точці А(xА, yА) чисельно дорівнює найменшій відстані від точки А до відрізка (відстань вимірюється по нормалі до відрізка). Останнє зауваження є наслідком основної властивості нормальних рівнянь.
Алгоритм побудови рівняння багатокутника складається з наступних етапів.
1. Пронумеруємо усі вершини n - кутника в напрямку проти руху годинної стрілки (починати можна з будь-якої вершини).
2. Запишемо орієнтовані рівняння F1 = 0, F2 = 0, F3 = 0 ,..., Fn-1 = 0 сторін n - кутника для кожної суміжної пари його вершин.
3. В отриманому наборі функцій F1, F2, F3, ..., Fn-1 виділимо дужками ті функції, що описують кожну з западин багатокутника. При цьому необхідно враховувати, що в западині може виявитися своя западина, що також необхідно виділити дужками.
4. У наборі F1, F2, F3, ..., Fn-1 (з дужками) необхідно зліва праворуч розставити знаки R-функцій Ú і Ù , починаючи зі знака R-кон’юнкції Ù . Необхідно враховувати, що при переході через дужку знак Ú змінюється на Ù , а знак Ù - на Ú . При цьому слід враховувати кратність запису дужок.
5. До рівняння простого багатокутника приходимо, дорівнявши нулю отриману функцію.
Приклад 1. Рівняння багатокутника, що зображено на рис. 6.1 а, має вид:
(F1 Ù F2 Ù F3) Ù F4 Ù (F5Ú F6) Ù (F7Ú F8) Ù F9 Ù (F10 Ú F11) = 0. (6.2)
Приклад 2. Рівняння багатокутника, що зображено на рис. 6.1 б, має вид:
F1 Ù (((F2 Ú F3) Ù F4) Ú F5 Ú F6 Ú
(F7 Ù F8 Ù F9)) Ù F10 Ù F11 Ù F12 = 0. (6.3)
Тут Fi - функції, що входять в орієнтовані рівняння сторін багатокутників.
Далі розглянемо варіант програмної реалізації запропонованого методу. Передбачається, що R-функції представлені як процедури-функції:
- R-диз'юнкція (аналог логічної операції об'єднання множин):
o(a, b) := (a + b + abs(a - b))/2;
- R-кон’юнкція (аналог логічної операції перетину множин):
p(a, b) := (a + b - abs(a - b))/2;
Тоді засобами процедур o(a,b) і p(a,b) ліву частину шуканого рівняння для функцій (6.2) представимо у виді:
F12 := p(F2, F1); F13 := o(F3, F12); F14 := o(F5, F6);
F15 := o(F7, F8); F16 := o(F10, F11); F13 := p(F13, F4);
F13 := p(F13, F14); F13 := p(F13, F15); f13 := p(F13, F9); (6.4)
F := p(F13, F16);
Рис. 6.1 - Приклади багатокутників
для опису рівняннями F(x, y) = 0
Алгоритм Рвачова гарантує, що утворена описаним способом функція F буде приймати додатні значення усередині, а від’ємні значення - поза багатокутником і дорівнювати нулю на сторонах цього багатокутника.
Унікальною особливістю середовища Maple V є те, що результат обчислень користувач одержує як у графічному, так і в аналітичному виді. Це можна здійснити після виконання наступної Maple - програми.
|
restart: with(plots): N := 11:
o := (a,b) -> (a + b + abs(a - b))/2:
p := (a,b) -> (a + b - abs(a - b))/2:
lin := (x1,y1,x2,y2,x,y) ->
(x*y1-x*y2-x1*y+x1*y2+x2*y-x2*y1)/
sqrt((y1-y2)^2+(x2-x1)^2):
x[1] := 7: y[1] := 3: x[2] := 1: y[2] := 3:
x[3] := -1: y[3] := 0: x[4] := -4: y[4] := 4:
x[5] := -6: y[5] := -1: x[6] := -4: y[6] := -2:
x[7] := -4: y[7] := -4: x[8] := 1: y[8] := -2:
x[9] := 4: y[9] := -4: x[10] := 7: y[10] := -3:
x[11] := 3: y[11] := 1: x[12] := 7: y[12] := 3:
for i from 1 to N do
f[i] := lin(x[i],y[i],x[i+1],y[i+1],x,y);
end do;
b1 := o(p(f[1],f[2]),f[3]):
b2 := p(f[4],o(f[5],f[6])):
b3 := p(f[9],o(f[7],f[8])):
b4 := o(f[10],f[11]):
F := (x,y) -> p(p(b1,b2), p(b3,b4)):
FF := (x,y) -> evalf(F(x,y),3): FF(x,y);
a := min(seq(x[i],i=1..N)): b := max(seq(x[i],i=1..N)):
c := min(seq(y[i],i=1..N)): d := max(seq(y[i],i=1..N)):
implicitplot(FF(x,y)=0, x=a-0.1..b+0.1, y=c-0.1..d+0.1,
numpoints = 3000,thickness=3,scaling=CONSTRAINED);
|
Початковими даними для виконання програми є координати вершин багатокутника. У результаті виконання програми будуть визначені нормальні рівняння сторін багатокутника:
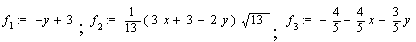
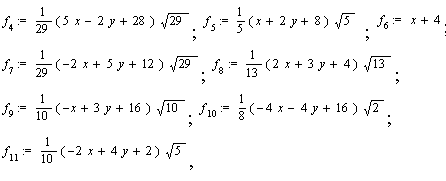 (6.5) (6.5)
опис результуючої функції, яка входить до рівняння багатокутника, та зображення багатокутника (рис.6.2).
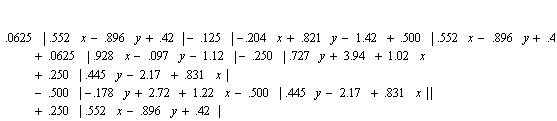 (6.6)
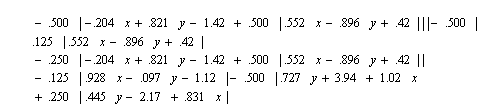
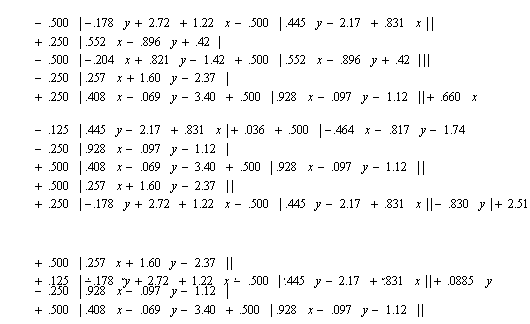
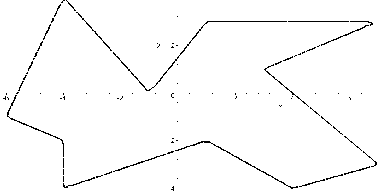
Рис.6.2 - Результат виконання Maple- програми (перший приклад)
Далі для порівняння наведемо програму опису та побудови багатокутника, що зображено на рис. 6.2 б.
|
restart: with(plots): N := 12:
o := (a,b) -> (a + b + abs(a - b))/2:
p := (a,b) -> (a + b - abs(a - b))/2:
lin := (x1,y1,x2,y2,x,y) ->
(x*y1-x*y2-x1*y+x1*y2+x2*y-x2*y1)/
sqrt((y1-y2)^2+(x2-x1)^2):
x[1] := -15: y[1] := -20: x[2] := 15: y[2] := -22:
x[3] := 5: y[3] := -12: x[4] := 10: y[4] := -3:
x[5] := -7: y[5] := -15: x[6] := -12: y[6] := 3:
x[7] := 0: y[7] := 15: x[8] := 5: y[8] := 3:
x[9] := 15: y[9] := 6: x[10] := 25: y[10] := 28:
x[11] := -12: y[11] := 25: x[12] := -40:y[12] := 0:
x[13] := -15: y[13] := -20:
for i from 1 to N do
f[i] := lin(x[i],y[i],x[i+1],y[i+1],x,y);
end do;
b1 := p(o(f[2],f[3]),f[4]):
b2 := p(p(f[7],f[8]),f[9]):
b3 := o(o(b1,b2),o(f[5],f[6])):
b4 := p(f[1],b3):
F := (x,y) -> p(p(f[10],f[11]),p(f[12],b4)):
FF := (x,y) -> evalf(F(x,y),3); FF(x,y);
a := min(seq(x[i],i=1..N)): b := max(seq(x[i],i=1..N)):
c := min(seq(y[i],i=1..N)): d := max(seq(y[i],i=1..N)):
implicitplot(FF(x,y)=0, x=a-0.1..b+0.1, y=c-0.1..d+0.1,
numpoints = 3000,thickness=3,scaling=CONSTRAINED); |
У результаті виконання програми за даними координатами вершин многокутника будуть визначенні нормальні рівняння сторін багатокутника
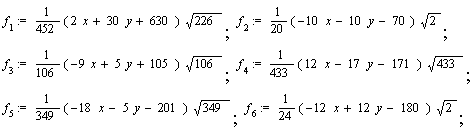 (6.7)
(6.7)
Також здійснюється побудова функції, що входить до рівняння многокутника:

(6.8)
На завершення виконується побудова багатокутника (рис.6.3)
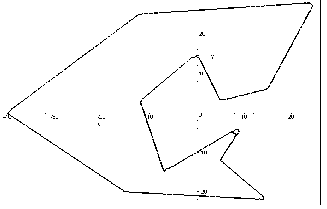
Рис.6.3 - Результат виконання Maple- програми (другий приклад)
|
|
|