|
|
Фронтом хвилі точкового джерела променів S у просторовій відбивальній системі {L, S} названо поверхню Ф, для всіх точок Q якої є однаковим шлях довільного променя, що надійшов з точки S до точки Q після відбиття від поверхні L в точці М.
Тобто фронтом вибухової хвилі Lt, що знаходиться на “відстані” t від джерела вибуху S, називається множина точок Q, які розташовані на відбитих від кривої L в точці M променях за умови, що SM + MQ = t для довільної точки М Î L.
Розглянемо циліндричну відбивальну поверхню L, профіль якої в декартовій системі координат Oxyz описано рівнянням z = k(1 - cos x). Джерело променів нехай має координати S(x0, y0, z0).
Крім того, вважається, що відбитий від поверхні L будь-який промінь не матиме з нею інших спільних точок (тобто вважається, що віддзеркалення від поверхні відбувається лише один раз).
|
> restart: with(plots):
> z0 := 0.7072: p := 0.7072:
> f := x -> p*(1.-cos(x)):
> df := unapply(D(f)(x),x):
> z := evalf(f(x)): x0 := 0.: y0 := 0:
> m := - df(x): n := 0.: l := 1.:
> k := ((x0-x)*m+(y0-y)*n+(z0-z)*l)/(m^2+n^2+l^2):
> x2:=2.*x-x0+2.*m*k:
> y2:=2.*y-y0+2.*n*k:
> z2:=2.*z-z0+2.*l*k:
> d01 := sqrt((x0-x)^2+(y0-y)^2+(z0-z)^2):
> d02 := sqrt((x2-x)^2+(y2-y)^2+(z2-z)^2):
> for t from 2 to 7 do
> X := simplify(x + (x2-x)*(2*t-d01) / d02, trig);
> Y := simplify(y + (y2-y)*(2*t-d01) / d02, trig);
> Z := simplify(z + (z2-z)*(2*t-d01) / d02, trig);
> GG[t] := plot3d([X,Y,Z], x=-Pi/2..Pi/2, y=0..2):
> od:
> gelob := plot3d(f(x), x=-Pi/2..Pi/2,
y=0..2,grid=[10,10]):
> display3d(
gelob,GG[2],GG[3],GG[4],GG[5],GG[6],GG[7]},
orientation=[130,80],scaling=CONSTRAINED,
shading=NONE, view=[-5.5..5.5,0..14,-1..14],
axes=BOXED); |
Рисунок 7.16 - Програма побудови сім’ї фронтів вибухової хвилі, яка утворилася після відбиття від циліндричної поверхні
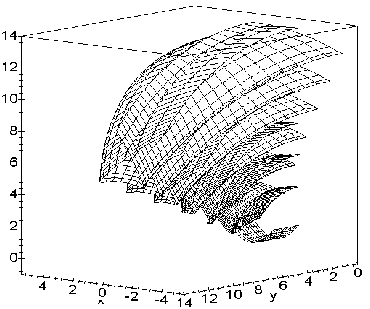
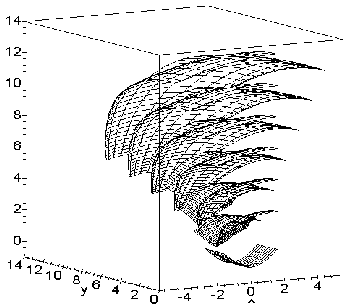
Співвідношення (7.9) покладено в основу програми (рис. 7.16) побудови наочних зображень елементів сім’ї фронтів вибухової хвилі. На рис. 7.17 для більш наочного сприйняття геометричної форми наведено два ракурси окремих фаз фронту хвилі вибуху.
|
|
|
|
Рисунок 7.17 - Два ракурси фронтів хвилі для циліндричної поверхні
z = 1- cos x і джерела променів в точці (0; 0; 1)
При цьому, як приклад, опис перерізу циліндричної поверхні мав вид z = 1 - cos x. Зображено лише симетричну половину фронтів, де джерелом є точка S(0; 0; 1).
Програма написана для середовища математичного процесора Maple V, що дозволило одержати й аналітичні описи сім’ї фронтів вибухової хвилі, в залежності від параметра t - як від шляху, пройденого елементами поверхні.
Твердження. Для циліндричної поверхні, рівняння профілю якої має вид z = k(1 - cos x), і точки S(0, 0, z0) як джерела променів описом фронтів ударної хвилі будуть вирази:
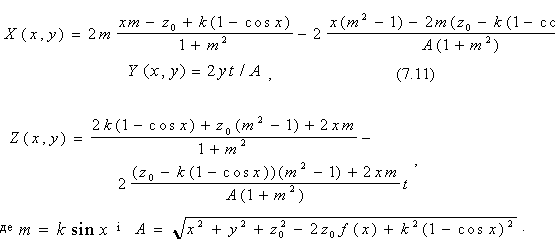
Твердження. Для циліндричної поверхні, профіль якої описано у виді z = - p cos x, і точки S(0, 0, z0) як джерела променів описом сім’ї фронтів ударної хвилі, що утворилася після відбиття від цієї поверхні, є:
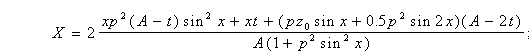

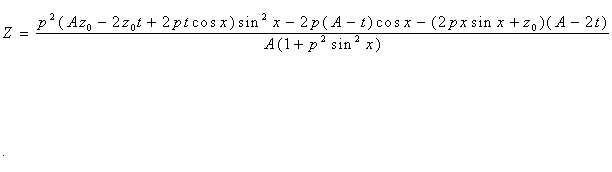
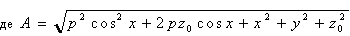
Конкретизуємо попередні твердження для випадку опису циліндричної поверхні у виді z = p (1- cos x) і коли p = z0 = 0,7072. Адже саме цей варіант викликає цікавість для розрахунку відбивальної системи, розглянутої в попередніх розділах. На рис. 7.18 наведено фрагмент програми (який необхідно використати для корекції програми рис. 7.16), а на рис. 7.19 зображено результати роботи відкорегованої програми.
Твердження. Для циліндричної поверхні з профілем у виді синусоїди z = 0,7072 (1- cos x) і точки S(0; 0; 0,7072) як джерела променів опис сім’ї фронтів ударної хвилі має вид:
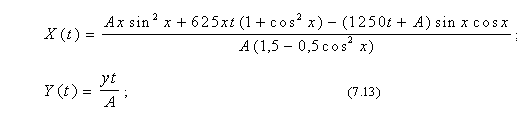
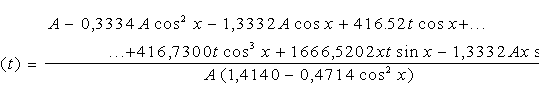
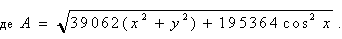
|
> A := sqrt(390625.*x^2+390625.*y^2+195364.*cos(x)^2);
> X := (x*A - x*A*cos(x)^2 + x*t*625 +
625.*x*t*cos(x)^2 - 1250.*sin(x)*cos(x)*t +
sin(x)*cos(x)*A)/A/(1.5 - 0.5*cos(x)^2);
> Y := y*t/sqrt(.25*x^2+.25*y^2+.1232517455*cos(x)^2);
> Z := (A-0.33339*A*cos(x)^2 -1.333216*cos(x)*A +
416.52019*cos(x)*t416.7399*cos(x)^3*t+
1666.52*x*sin(x)*t-.333216*x*sin(x)*A)
/A/(1.414027226-.4714252315*cos(x)^2); |
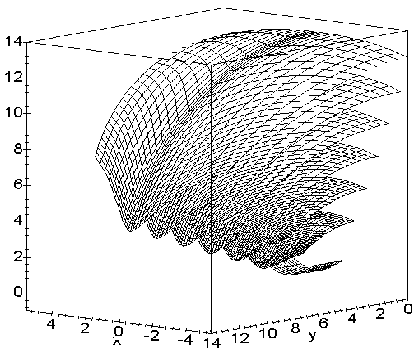
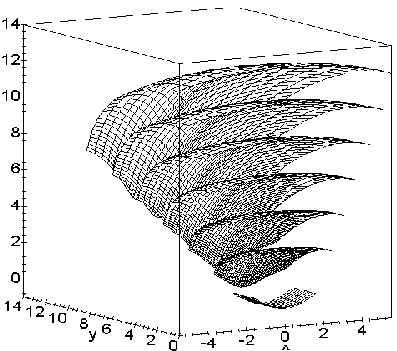
Рисунок 7.19 - Два ракурси симетричної частини фронтів хвилі для циліндричної поверхні z = 0,7072(1- cos x)
і джерела (0; 0; 0,7072)
До позитивних якостей графічного представлення поверхонь вибухових хвиль слід віднести те, що є можливість порівнювати інтенсивності дії хвилі за її конфігурацією та розмірами. На практиці зручно порівнювати площі елементарних просторових чотирикутників, які складають поверхню хвилі: чим більшою є площа чотирикутника, тим меншу інтенсивність дії хвилі він забезпечує.
Дійсно, наочно можна переконатися у тому, що інтенсивність ударної хвилі для параболічного циліндра буде більшою, порівняно з синусоїдальним циліндром. На це вказує “густина” координатних ліній поверхонь, яка припадає на одиницю об’єму простору. Переконатися в цьому можна, порівнюючи, наприклад, рисунки 7.17 і 7.19.
Наведене положення базується на тому, що ударна хвиля у необмеженому просторі матиме вид сфери радіусом R з центром в точці вибуху. Площа поверхні сфери дорівнюватиме 4p R2/3 одиниць. При цьому вся інтенсивність вибуху буде немов “розтерта”, розподілена по поверхні сфери. Тоді в певній точці поверхні сфери інтенсивність вибуху з точністю до множника можна оцінити величиною W = 1/(4p R2/3), тобто залежністю 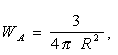
яка виражає залежність виду “обернено пропорційно квадрату відстані” і узгоджується з загальнофізичними законами ослаблення поля в залежності від відстані.
Розглянутий приклад дозволяє прийняти гіпотезу досліджень: інтенсивність дії ударної хвилі є величиною, оберненою до площі поверхні ділянок фронтів хвилі, які підпорядковані до закону гомотетії. На рис. 7.20 -7.22 наведено приклади поверхонь хвиль, відбитих від циліндричної поверхні, в залежності від положення джерела вибуху. Зображення дозволяють “якісно” порівнювати інтенсивності їх дії. Далі розглянуто кількісні характеристики
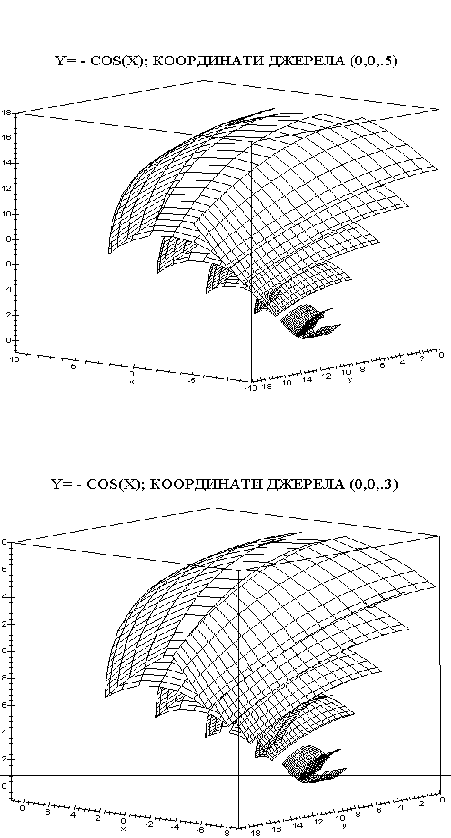
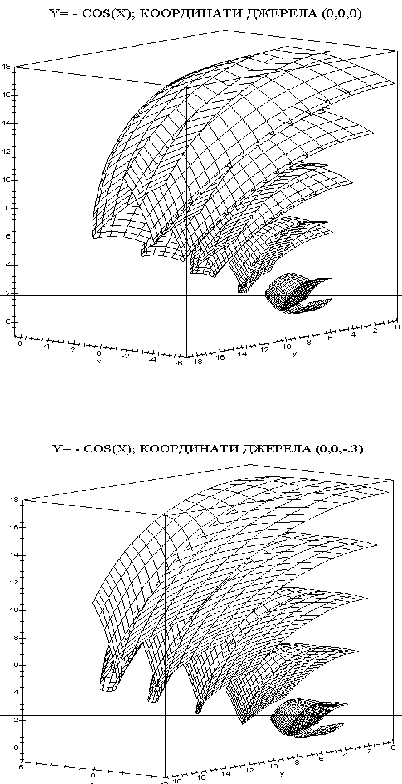
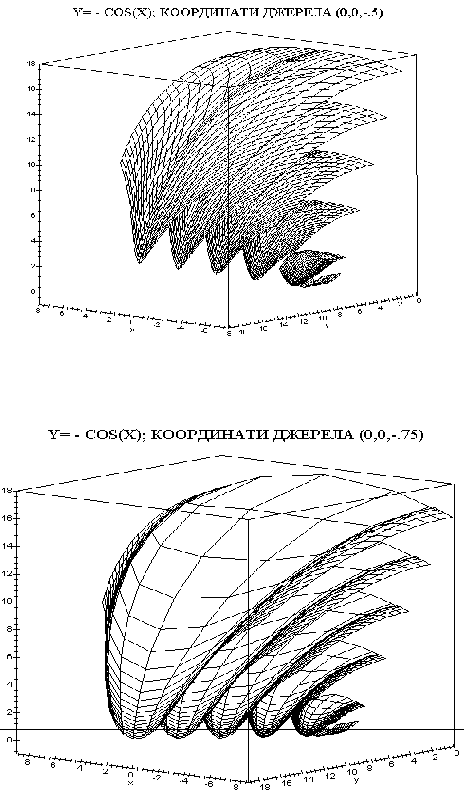
Рисунок 7.22 - Приклади хвиль, відбитих від циліндричної поверхні
|