|
|
4.2 Рух елементарної частки у центральному полі сил
Як відомо, задачу про рух двох тіл можна звести до задачі про рух одного тіла в “гравітаційному” полі другого тіла. В результаті чого виникає питання про визначення руху частки в зовнішньому полі, у якому її потенційна енергія залежить тільки від відстані r до визначеної нерухомої точки - джерела поля. Зазначимо, що таке поле називають центральним.
Сила 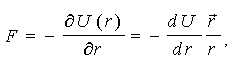 , яка , яка діє на частку, за абсолютною величиною залежить при цьому теж тільки від відстані r і спрямована в кожній точці уздовж радіуса-вектора ` r.
Також відомо, що при русі в центральному полі зберігається момент системи щодо центра поля. Для однієї частки це є M = [` r p ].
Оскільки вектори М і ` r взаємно перпендикулярні, сталість М означає, що при русі частки її радіус-вектор` r увесь час залишається в одній площині, яка є перпендикулярною до М.
Таким чином, траєкторія руху частки в центральному полі лежить цілком в одній площині. Ввівши в ній полярні координати r та j , напишемо функцію Лагранжа у виді
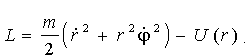 . (4.1) . (4.1)
Ця функція не містить у явному виді координату j . Всяку узагальнену координату qi , яка не входить явно в лагранжеву функцію, називають циклічною. Враховуючи рівняння Лагранжа для такої координати, маємо тотожність: 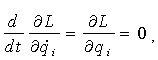 , тобто відповідний їй узагальнений імпульс , тобто відповідний їй узагальнений імпульс  є інтегралом руху. Ця обставина приводить до істотного спрощення задачі інтегрування рівнянь руху за наявності циклічних координат. є інтегралом руху. Ця обставина приводить до істотного спрощення задачі інтегрування рівнянь руху за наявності циклічних координат.
У даному випадку узагальнений імпульс 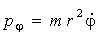 збігається збігається з моментом Mz = M, оскільки має місце закон збереження моменту:
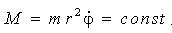 . .
(4.2)
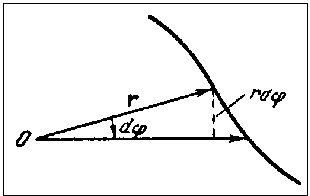
Рис. 4.5 - Параметри руху частки
Зазначимо, що для плоского руху однієї частки в центральному полі цей закон допускає просту геометричну інтерпретацію. Вираз 0,5` r r dj являє собою площу сектора, утвореного двома нескінченно близькими радіусами-векторами й елементом дуги траєкторії (рис. 4.5). Позначивши її як df, напишемо момент частки у вигляді:
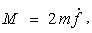 , (4.3) , (4.3)
де похідну 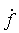 називають секторіальною швидкістю. Тому збереження моменту означає сталість секторіальної швидкості - за рівні проміжки часу радіус-вектор називають секторіальною швидкістю. Тому збереження моменту означає сталість секторіальної швидкості - за рівні проміжки часу радіус-вектор точки, що рухається, описує рівні площі (це є так званий другий закон Кеплера). Закон збереження моменту для частки, що рухається у центральному полі, іноді називають інтегралом площ.
Повний розв’язок задачі про рух частки у центральному полі найпростіше одержати, виходячи з законів збереження енергії і моменту, не виписуючи при цьому самих рівнянь руху. Виражаючи 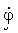 через M з (4.2) і підставляючи у вираз для енергії, одержимо: через M з (4.2) і підставляючи у вираз для енергії, одержимо:
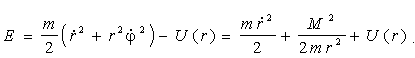 . (4.4) . (4.4)
Звідси
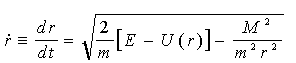 (4.5) (4.5)
або, розділяючи змінні й інтегруючи:
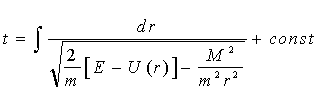 . (4.6) . (4.6)
Далі, записавши (4.2) у вигляді 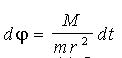 і підставивши сюди dt з (4.5) й інтегруючи, знаходимо: і підставивши сюди dt з (4.5) й інтегруючи, знаходимо:
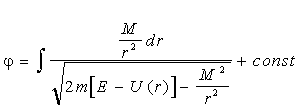 . (4.7) . (4.7)
Формули (4.6) і (4.7) дають розв’язок у загальному виді поставленої задачі. Друга з них визначає зв'язок між r і j , тобто рівняння траєкторії. Формула ж (4.6) визначає в неявному виді відстань r точки, що рухається, від центра як функцію часу. Відзначимо, що кут j змінюється у часі монотонним чином - з (4.2) видно, що  ніколи не змінює знака. ніколи не змінює знака.
Вираз (4.4) показує, що радіальну частину руху можна розглядати як одномірний рух у полі з “ефективною” потенційною енергією:
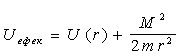 . (4.8) . (4.8)
Величину 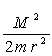 називають відцентровою енергією. Значення r, при яких називають відцентровою енергією. Значення r, при яких
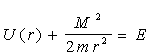 (4.9) (4.9)
визначають границі області руху по відстані від центра. При виконанні рівності (4.9) радіальна швидкість 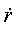 дорівнює нулю. Це не означає зупинки частки (як при “відвертому” одномірному русі), тому що кутова швидкість дорівнює нулю. Це не означає зупинки частки (як при “відвертому” одномірному русі), тому що кутова швидкість 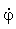 не перетворюється на нуль. Рівність не перетворюється на нуль. Рівність 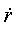 = 0 означає точку повороту траєкторії, у якій функція r(t) переходить від збільшення до зменшення чи навпаки. = 0 означає точку повороту траєкторії, у якій функція r(t) переходить від збільшення до зменшення чи навпаки.
Якщо область допустимої зміни r обмежена лише однією умовою r ³ rmin, то рух частки є інфінітним - тобто її траєкторія приходить з нескінченності й іде на нескінченність.
Якщо область зміни r має двi границi rmin і rmax, то рух є фінітним і траєкторія цілком лежить усередині кільця, обмеженого колами r = rmax і r = rmin. Це, однак, не означає, що траєкторія неодмінно є замкнутою кривою. За час, протягом якого r змінюється від rmax до rmin і потім знову до rmax, радіус-вектор повернеться на кут D j , рівний згідно (4.7):
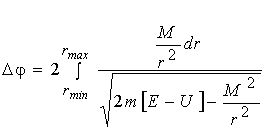 . (4.10) . (4.10)
Умова замкнутості траєкторії полягає у тому, щоб цей кут дорівнював раціональній частині від 2p , тобто можна записати D j = 2p n1/n2, де n1 , n2 - цілі числа. Тоді через n2 повторень цього періоду часу радіус-вектор точки, зробивши n1 повних оборотів, співпаде зі своїм первісним значенням, тобто траєкторія замкнеться.
Існують лише два типи центральних полів, у яких усі траєкторії фінітних рухів замкнуті. Це поля, у яких потенційна енергія частки пропорційна 1/r чи r2. Перший з цих випадків розглянемо далі. Він має назву Кеплерової задачі.
Найважливішим випадком є центральні поля, у яких потенційна енергія обернено пропорційна r. Сюди відносяться ньютонівські поля тяжіння і кулонівські електростатичні поля; перші, як відомо, мають характер тяжіння, а другі можуть бути як полями тяжіння, так і відштовхування.
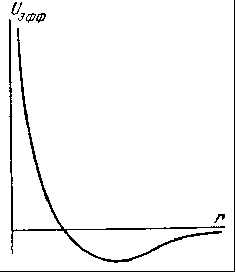
Рис. 4.6 – Графік потенційної енергії
Розглянемо поле тяжіння, у якому
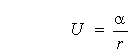 (4.11) (4.11)
с додатною постійною a . Графік “ефективної” потенційної енергії:
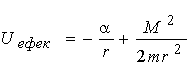 (4.12) (4.12)
має вид, зображений на рис. 4.8. При r ® 0 енергія прямує до +¥ , а при r ® ¥ енергія прямує до нуля; при r = M 2/a m — енергія має мінімум, рівний
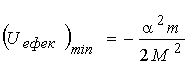 . (4.13) . (4.13)
З цього графіка відразу стає очевидним, що при Е ³ 0 рух частки буде і нфінітним, а при E < 0 — фінітним.
Форму траєкторії знаходять за допомогою формули (4.7). Підставляючи в неї U = -a / r і зробивши елементарне інтегрування, одержимо: 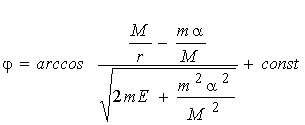 . Обираючи початок відліку кута j так, щоб const = 0, і вводячи позначення . Обираючи початок відліку кута j так, щоб const = 0, і вводячи позначення
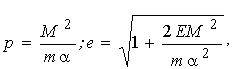 , (4.14) , (4.14)
перепишемо формулу для траєкторії у виді:
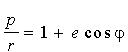 . (4.15) . (4.15)
Це рівняння конічного перетину з фокусом в початку координат; р і е - так звані параметр і ексцентриситет орбіти. Зроблений нами вибір початку відліку j полягає, як видно з (4.15), у тому, що точка з j = 0 є найближчою до центра.
В еквівалентній задачі двох тіл, які взаємодіють за законом (4.11), орбіта кожної з часток теж являє собою конічний перетин з фокусом у їхньому спільному центрі інерції.
З (4.14) видно, що при Е < 0 ексцентриситет е < 1, тобто орбіта є еліпсом (рис. 4.7) і рух є фінітним. Відповідно до відомих формул аналітичної геометрії, маємо формули опису великої і малої півосі еліпса:
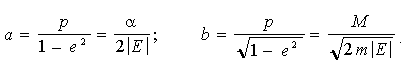 (4.16) (4.16)
Найменш допустиме значення енергії збігається з (4.13), при цьому е = 0, тобто еліпс перетворюється на коло. Відзначимо, що велика піввісь еліпса залежить тільки від енергії (але не від моменту) частки. Найменша і найбільша відстані до центра поля (фокуса еліпса) рівні:
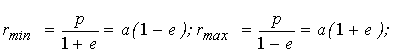 (4.17) (4.17)
Ці вирази (з а і е з (4.16) і (4.14)) можна було б, звичайно, одержати і безпосередньо як корені рівняння Uефек (r) = E.
Час обертання по еліптичній орбіті, тобто період руху Т, зручно визначити за допомогою закону збереження моменту у формі “інтеграла площ” (3). Інтегруючи цю рівність за часом від нуля до Т, одержимо 2mf = TM, де f - площа орбіти. Для еліпса маємо тотожність f = p ab і за допомогою формул (4.16) знаходимо:
 . (4.18) . (4.18)
Відзначимо, що період залежить тільки від енергії частки. При цьому квадрат періоду пропорційний кубу лінійних розмірів орбіти (це є так званий третій закон Кеплера).
|
|
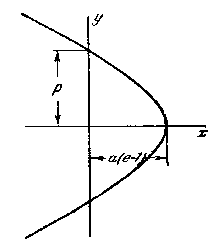
|
|
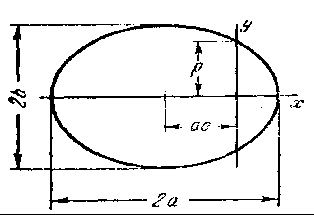
Рис. 4.7 - Параметри еліптичної траекторії |
Рис. 4.8 - Параметри гіперболи |
При Е ³ 0 рух є інфінітним. Якщо E > 0, то ексцентриситет e > 1, тобто траєкторія є гіперболою, що огинає центр поля (фокус), як показано на рис. 4.8. Найближча відстань до центра:
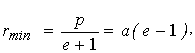 , (4.19) , (4.19)
де 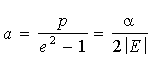 - “піввісь” гіперболи. - “піввісь” гіперболи.
У випадку ж Е = 0 ексцентриситет е = 1, тобто частка рухається по параболі, з мінімальною відстанню rmin = р/2. Цей випадок має місце, якщо частка починає свій рух зі стану спокою на нескінченності.
Далі розглянемо випадок руху частки у полі відштовхування:
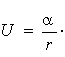 . .
(4.20)
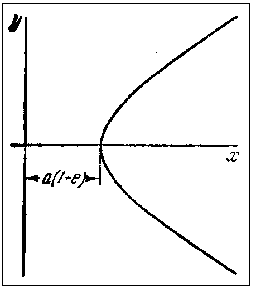
Рис. 4.9 - Гіперболічний трек
У цьому випадку (при a > 0) ефективну потенційну енергію можна обчислити за формулою 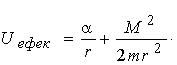 . Легко перевірити, що . Легко перевірити, що 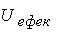 монотонно убуває від + ¥ до нуля при зміні r від нуля до ¥ . монотонно убуває від + ¥ до нуля при зміні r від нуля до ¥ .
Енергія частки може бути тільки додатною, і рух завжди є інфінітним. Всі обчислення для цього випадку в точності аналогічні зробленим вище. Траєкторія є гіперболою (чи параболою при E = 0) . (Тут р і е визначаються за формулами (4.14)) і проходить повз центр поля, як показано на рис. 4.11. Мінімальна відстань до центра 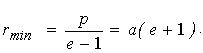 . .
Таким чином, ми дійшли висновку, що для побудови треку a - частки необхідно здійснити складний аналіз стосовно параметрів часток та параметрів їх переміщення. Далі буде показано, що можна уникнути цього аналізу, коли треки визначати за допомогою розв’язання диференціального рівняння.
|
|
|