|
При проектуванні шнекових пресів для роздрібнення вогнегасного порошку виникає задача профілювання пари насадок, кожна з яких має форму фігури постійної ширини - криволінійного трикутника Релло. При цьому мається на увазі, що пара насадок обертається синхронно (тобто в один і той же бік). Необхідно скласти алгоритм геометричного моделювання обертання пари трикутників Релло так, щоб в процесі обертання здійснювався лише точковий дотик.
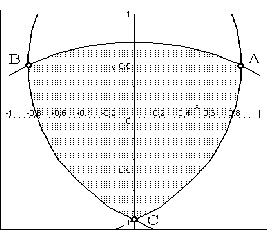
Рис. 3.3 - Трикутник Релло
Нагадаємо, що фігурою постійної ширини називається опукла фігура, для якої є однаковими відстані між довільними парами опорних (тобто дотичних до контуру) паралельних прямих.
Існує безліч фігур постійної ширини H, відмінних від кола з діаметром H. Найпростішою з фігур постійної ширини є трикутник Релло. Він утворений у результаті перетину трьох кругів радіуса H, центри яких розташовано у вершинах A, B i C рівностороннього трикутника зі сторонами H (рис.3.3).
Далі розглянуто метод опису трикутника Релло рівнянням у вигляді F(x, y) = 0. Для цього використовувалися як традиційні (бінарні) R-кон’юнкції, так і запропоновані тримісні R-кон’юнкції.
Нехай радіус кола, описаного навколо трикутника Релло, дорівнює a. Тоді легко переконатися у тому, що три кола, які складають периметр трикутника Релло, мають рівняння6
;
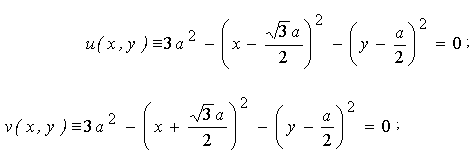 ; ( ; (
3.2)
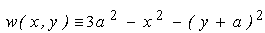
Опис трикутника Релло - як результату перетину трьох кругів - можна здійснити, двічі застосувавши R-кон’юнкцію вигляду:
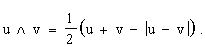 . .
Але ця R-операція є двомісною, адже вона залежить від двох величин u i v. Бінарний характер R-операцій сприяє нерівнозначному входженню компонентів опису у результуючу формулу. Дійсно, для R-кон’юнкції трьох величин u, v і w маємо вираз:
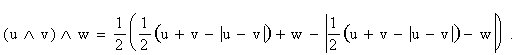 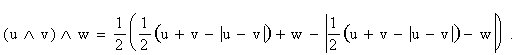 . (3 . (3
.3)
Недолік формули ( 3.3) виявляється у “несиметричному” входженні рівнозначних за смислом параметрів u, v і w. Крім того, на вигляд аналітичного виразу впливає і послідовність дій з обраними парами аргументів.
Приклад 1. Послідовність операцій (u Ù v) Ù w дає перший варіант рівняння трикутника Релло (тут і далі радіус описаного кола а = 1):
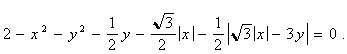 ( (
3.4)
Приклад 2. Послідовність операцій (v Ù w) Ù u дає другий варіант рівняння трикутника Релло
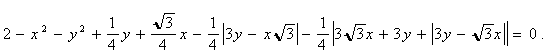 ( (
3.5).
Приклад 3. Послідовність операцій (u Ù w) Ù v дає третій варіант рівняння трикутника Релло
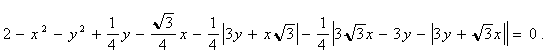 ( (
3.6)
Крім того, середнє арифметичне значення виразів, що містяться в лівих частинах рівнянь (4) - (6), дає можливість одержати “майже” симетричний опис трикутника Релло відносно входження величин u, v i w.
Приклад 4. Послідовність операцій
[((u Ù v) Ù w) + ( (v Ù w) Ù u ) + ((u Ù w) Ù v)] /3
дає четвертий варіант рівняння трикутника Релло:
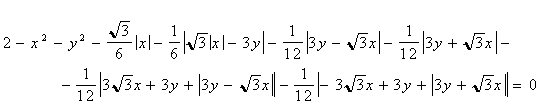 .( .(
3.7)
Наведені приклади неоднозначного опису трикутника Релло ілюструють недоліки опису трикомпонентних об’єктів за допомогою бінарної (двомісної) R-кон’юнкції.
Усунути зазначені недоліки в роботі пропонується за допомогою тримісних R-операцій.
Перш ніж визначити тримісну R-кон’юнкцію, нагадаємо, яким чином можна одержати бінарні R-кон’юнкцію 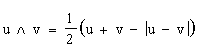 та R-диз’юнкцію та R-диз’юнкцію 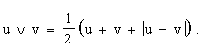 . .
В роботі [ 6] показано, що u Ù v = min(u, v) i u Ú v = max(u, v). Легко переконатися у тому, що виконуються співвідношення:
uv = min(u, v) max(u, v);
u + v = min(u, v) + max(u, v).
Тоді за теоремою Вієта можна скласти квадратне рівняння:
T2 - (u + v) T + u v = 0. ( 3.8)
Корені квадратного рівняння ( 3.8) визначаються формулами 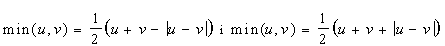 . Звідси маємо бінарні операції R-кон’юнкції та R-диз’юнкції. . Звідси маємо бінарні операції R-кон’юнкції та R-диз’юнкції.
За аналогією можна ввести і тримісні R-операції. Позначимо через min(u, v, w), max(u, v, w) та mid(u, v, w) відповідно мінімальне, максимальне та середнє за величиною серед чисел u, v та w. Знайдемо формули у вигляді функції трьох змінних, за якими можна обчислювати значення min, max та mid.
Легко переконатися у тому, що виконуються наступні тотожності:
min(u, v, w) + mid(u, v, w) + max(u, v, w) = u + v + w;
min(u, v, w) mid(u, v, w) + min(u, v, w) max(u, v, w) +
+ mid(u, v, w) max(u, v, w) = u v + uw + vw; ( 3.9)
min(u, v, w) mid(u, v, w) max(u, v, w) = u v w.
Тому за теоремою Вієта величини min(u, v, w), max(u, v, w) та mid(u, v, w) можна вважати мінімальним, максимальним та середнім за величиною коренями кубічного рівняння:
T3 - (u + v + w) T2 + (u v + uw + vw) T - u v w = 0. ( 3.10)
Зробимо заміну T = H + (u + v + w) / 3. Тоді рівняння ( 3.10) набуде вигляду:
(3 H + u + v - 2w)( 3 H + u + w - 2v)( 3 H + v + w - 2u) = 0 ( 3.11)
або
H3 + p H + q = 0, ( 3.12)
де p = (uv + uw + vw - u2 - v2 - w2) / 3
q = (2u - v - w)(2v - u - w)(2w - u - v) / 27.
Позначимо через S = - p / 27, тобто
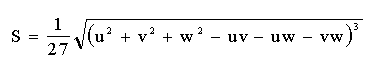 і через a = arccos(- q / (2 S)), тобто і через a = arccos(- q / (2 S)), тобто
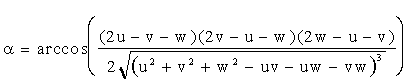 . .
В результаті маємо вирази для обчислення коренів кубічного рівняння ( 3.10):
max = 2 S1/3 cos(a / 3) + (u + v + w) / 3;
mid = 2 S1/3 cos((a +4p ) / 3) + (u + v + w) / 3; ( 3.13)
min = 2 S1/3 cos((a +2p ) / 3) + (u + v + w) / 3.
Або
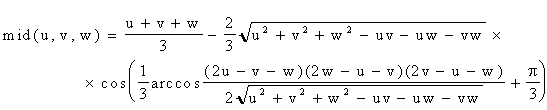 ; ;
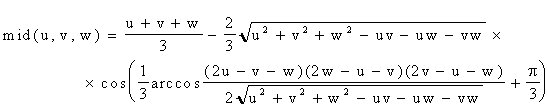 ; ;
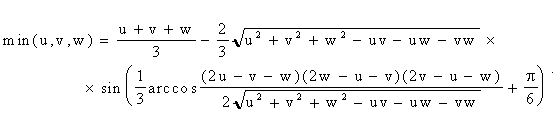 . .
Тримісну R-операцію mid, яка дозволяє визначати середнє за величиною серед трьох чисел, пропонується назвати R-мід’юнкцією.
Приклад 5.
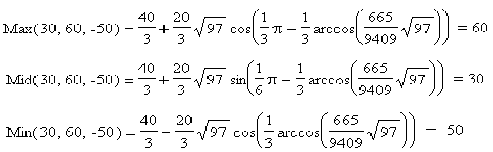
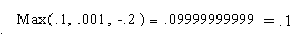
Приклад 6.

Звідси маємо основні твердження роботи.
Твердження 1. Опис тримісної R-кон’юнкції має вигляд:
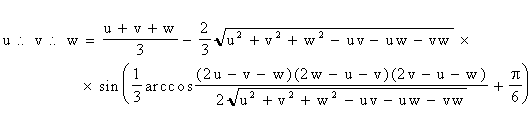 ( (
3.14)
Застосування тримісної операції R-кон’юнкції ( 3.14) дає рівняння трикутника Релло u(x, y) v(x, y) w(x, y) = 0.
Твердження 2. Нехай радіус кола, яке описано навколо трикутника Релло, дорівнює a, і полюс трикутника збігається з початком координат. Якщо трикутник Релло повернути проти напряму стрілки годинника навколо полюса на кут a , то його рівняння матиме вид:
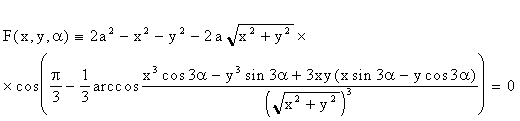 (3.15)
Приклад 8. При a = 1 і a = 0 маємо
 . .
Приклад 9. При a = 1 і a = p /6 маємо
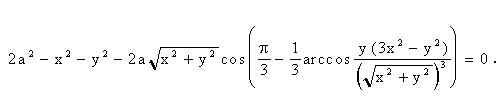
Для перевірки одержаної формули було складено програму мовою Maple V. На рис. 3.4 наведено програму побудови трикутника Релло та результат її виконання.
> restart: with(plots):
> a := 1: alpha := Pi/12:
> f :=
2*a^2-y^2-x^2-2*a*sqrt(x^2+y^2)*cos(Pi/3-
arccos((x^3*cos(3*alpha)+3*y*x^2*sin(3*alpha)-
3*x*y^2*cos(3*alpha)-y^3*sin(3*alpha))/
sqrt(y^6+3*x^2*y^4+3*x^4*y^2+x^6))/3):
> f:= simplify(f);
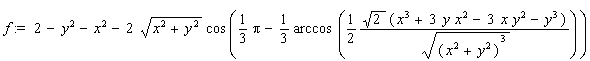
> implicitplot(f(x,y),x=-a..a,y=-a..a,
scaling=CONSTRAINED, thickness=3, grid=[25,25]);
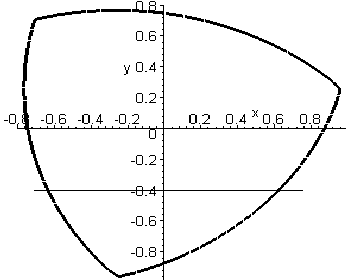
Рис. 3.4 - Програма побудови трикутника Релло
|