В перекладі слово сплайн означає “гнучка лінійка”, яку деформують так, щоб по ній можна було провести криву через задані точки (xi, yi). Будучи деформована таким чином, лінійка набуває форми, при якій запасена в ній пружна енергія є мінімальною. Використовуючи теорію згину бруса за малих деформацій, можна точно показати, що сплайн - це група сполучених кубічних многочленів, у місцях сполучення яких перша і друга похідні неперервні. Об’єднання таких функції і називають кубічними сплайнами. Для побудови сплайну необхідно задати коефіцієнти, що єдиним чином визначають кубічний многочлен у проміжку між даними точками.
У найпростішому випадку необхідно задати всі кубічні функції q1(x), q2(x), ..., qm(x). У найбільш загальному випадку ці многочлени мають вигляд qi(x) = k1i + k2ix + k3ix2 + k4ix3, i = 1, 2, ..., m, де kji — незмінні, обумовлені зазначеними вище умовами.
Перші 2т умов вимагають, щоб сплайни стикалися в заданих точках
qi(xi) = yi, i = 1, ..., m; qi+1(xi) = yi, i = 0, ..., m - 1.
Наступні 2т—2 умов вимагають, щоб у місцях зіткнення сплайнів були рівні перші і другі похідні:
q¢ i+1(xi) = q¢ i(xi), i = 1, ..., m - 1, q² i+1(xi) = q² i(xi), i = 0, ..., m - 1.
Щоб система алгебраїчних рівнянь мала розв’язок, необхідно, щоб число рівнянь точно дорівнювало числу невідомих. На даному етапі ми маємо 4m невідомих і 4m - 2 рівнянь. Отже, ми повинні знайти ще два рівняння. Звичайно використовують рівняння q² 1(x0) = 0 i q² m(xm) = 0.
Визначений таким чином сплайн називають звичайним кубічним сплайном. Знайшовши коефіцієнти сплайна, можна використовувати цю кусочно-гладку поліноміальну функцію для представлення даних при інтерполяції.
На перший погляд може показатися, що визначення коефіцієнтів зводиться до розв’язання 4m рівнянь з 4m невідомими. Однак, шляхом вибору виду кубічних многочленів цю задачу можна значно спростити. Так, коли окремі кубічні рівняння мають вид:
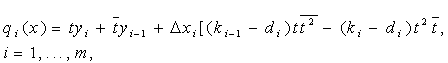(2.1)
де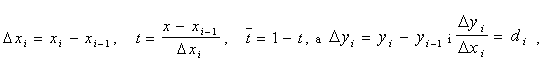 
,
то кожне з рівнянь qi(х) містить тільки два незмінних невідомих коефіцієнти. Після того, як перше рівняння qi(х) записано, з кожним наступним рівнянням додається тільки один новий невідомий коефіцієнт. При цьому при х = xi-1 t = 0,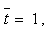 
, а при x =xi 
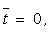, t = 1. При такому виборі кубічних многочленів автоматично задовольняються всі умови, крім умов, що накладаються на другі похідні. Для внутрішніх точок виконується співвідношення
ki-1D xi+1 + 2ki(D xi + D xi+1) + ki+1D xi = 3(diD xi+1 + di+1D xi), (2.2)
а для двох зовнішніх — співвідношення
2k0 + k1 = 3d1 i km-1 + 2km = 3dm . (2.3)
Таким чином, система рівнянь, що розв’язується, є лінійною, а її матриця є тридіагональною:
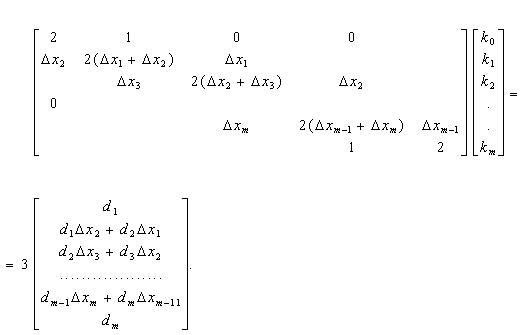
(2.4)
У системі рівнянь (2.4) число обумовлених коефіцієнтів дорівнює числу заданих точок. Тому розв’язок виявляється не більш складним, ніж у випадку апроксимації m+1 точок многочленом m-го степеня.
У багатьох роботах наголошується, що кубічний сплайн апроксимує функцію краще, ніж многочлен степеня т. Тому далі при розробці програмного забезпечення визначення форми розпорошення вогнегасної речовини ми будемо застосовувати саме сплайни.