|
|
Нехай струмінь води з пожежного ствола спрямовано під кутом a до горизонту за умови, що він рухається в середовищі, опір якого пропорційний швидкості v елементарної частки струменя (рис. 1.2). Необхідно визначити траєкторію руху цього струменя.
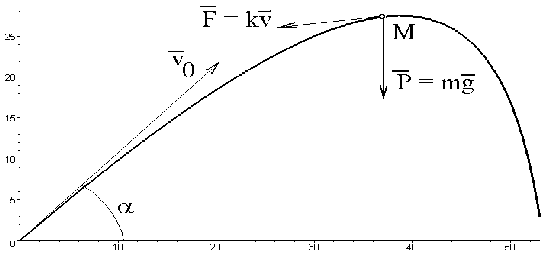
Рис. 1.2 - Траєкторія струменя з урахуванням опору повітря
Виберемо елементарну частку струменя. У будь-якій точці М (х,у) траєкторії руху частки на неї діють дві сили: вага частки Р = mg і опір середовища F = kv.
Складові їх рівнодіючої по осях координат:
X = Р cos (Р; х) + F cos (F; x), ( 1.11)
Y = P cos (Р; у) + F cos (F; y).
Але cos (Р; х) = 0, cos (Р; у) = 1, cos (F; х) = - dx / dS , cos (F; у) = - dy / dS. Отже,
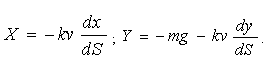 ; . (1.12) ; . (1.12)
Як відомо, v = dS / dt. Тоді система приймає остаточний вигляд:
;
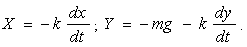 . (1.13) . (1.13)
Використовуючи другий закон динаміки, одержимо диференціальне рівняння руху:
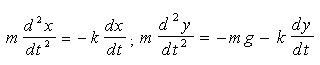
або
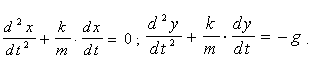 (1.14) (1.14)
Розв’язуючи перше рівняння системи як лінійне однорідне, а друге як лінійне неоднорідне рівняння другого порядку, одержимо загальний розв’язок системи:
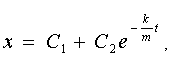 , (1.15) , (1.15)
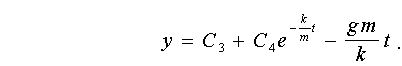
Використовуючи при t = 0 початкові умови
х = 0, у = 0, dx / dt = v0 cos a , dy / dt = у0 sin a , (1.16)
знайдемо значення довільних постійних:
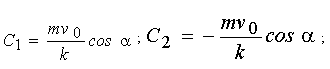
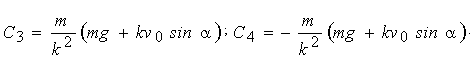 (1.17) (1.17)
Підставляючи знайдені значення C1, C2, С3, С4 у загальне рішення системи, одержимо часткове рішення:
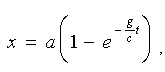 , (1.18) , (1.18)
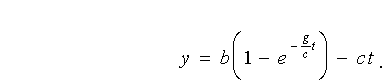
З виразу для x у формулі (1.18) маємо . Підставляючи замість 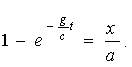 його значення x / a у вираз для у, одержимо його значення x / a у вираз для у, одержимо 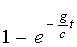 відкіля відкіля  . Вираз для часу t підставляємо у формулу для х і одержуємо: . Вираз для часу t підставляємо у формулу для х і одержуємо:
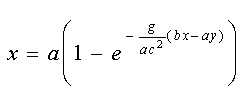 , (1.19) , (1.19)
відкіля
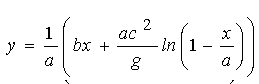 . (1.20) . (1.20)
Це і є остаточне рівняння траєкторії руху струменя з урахуванням фактору повітря, опір якого пропорційний швидкості v елементарної частки цього струменя. Зазначимо, що екстремальне значення висоти траєкторії
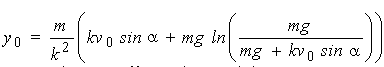 (1.21) (1.21)
досягається у точці
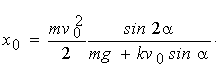 . (1.22) . (1.22)
Для перевірки формули (1.20) було складено Maple-програму (рис.1.3). Деякі результати розрахунків наведено на рис. 1.4 - 1.7.
restart: with(plots):
alf := 0.8: v0 := 50: g :=9.8:
k := 0.5: m := 0.8:
a := m*v0*cos(alf)/k;
b := m*(m*g+k*v0*sin(alf))/k^2;
c := m*g/k;
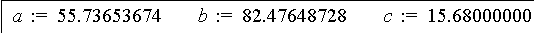
y := simplify((b*x+a*c^2*ln(1-x/a)/g )/a);
plot(y(x),x=0..53, scaling = CONSTRAINED,thickness=3);
df := diff(y,x);
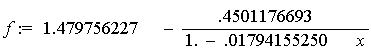
sol := solve({df},{x}): assign(sol): x0 := x;
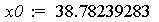
y0 := simplify(y(x));
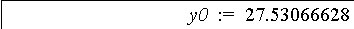
Рис.1.3 - Програма побудови траєкторії руху струменя води
з урахуванням опору повітря
Рис.1.4 - Траєкторії руху струменя води,
коли змінним є кут нахилу ствола
Рис.1.5 - Траєкторії руху струменя води,
коли змінним є коефіцієнт опору повітря
Рис.1.6 - Траєкторії руху струменя води,
коли змінною є маса елементарної частки струменя
Рис.1.7 - Траєкторії руху струменя води,
коли змінною є початкова швидкість вильоту струменя
|
|
|