|
Наведемо огляд деяких робіт, де пропонуються математичні моделі руху елементарної частки вогнегасної речовини, що базуються на розв’язанні системи диференціальних рівнянь. Ці моделі дозволяють більш адекватно описувати траєкторію струменя води з урахуванням опору повітря та інших факторів, які впливають на форму траєкторії.
В роботі Бикова С.О. [3] розглянуто ефективну технологію дальнього розпорошення вогнегасних речовин. При цьому аналіз особливостей руху елементарної частки вогнегасної речовини після вильоту зі ствола імпульсного вогнегасника показав, що можна використовувати таку схематизацію руху частки, при якій можна розглядати не хмару цих часток у цілому, а рух одиночної порошкової частки з аналогічними початковими умовами.
Рівняння, що описують рух порошкової частки, записані при наступних допущеннях: на порошкову частку діє сила тяжіння і сила аеродинамічного опору; розмір порошкової частки постійний; порошкова частка має сферичну форму; порошкова частка енергоізольована та ізотермічна; сила аеродинамічного опору визначається з умови обтікання порошкової частки газом у момент часу t 0; порошкова частка рухається в нерухомому газовому середовищі з параметрами, аналогічними атмосферним за нормальних умов.
Для математичного опису процесу прийнято наступне припущення: у початковий момент часу швидкість порошкової частки Vч = V0, кут нахилу вектора швидкості частки до обрію b = b о, діаметр частки dч = соnst.
Рівняння, що описує рух порошкової частки у векторній формі, має вид  , де а - прискорення порошкової частки, м /с2; G = Мg -сила тяжіння, Н; R - М-КWК2 - сила аеродинамічного опору повітря, що направлена по дотичній в бік, протилежний рухові, H; К -- коефіцієнт аеродинамічного опору, м -1. , де а - прискорення порошкової частки, м /с2; G = Мg -сила тяжіння, Н; R - М-КWК2 - сила аеродинамічного опору повітря, що направлена по дотичній в бік, протилежний рухові, H; К -- коефіцієнт аеродинамічного опору, м -1.
Траєкторію польоту частки порошку умовно розділили на дві ділянки (рис 1.7).
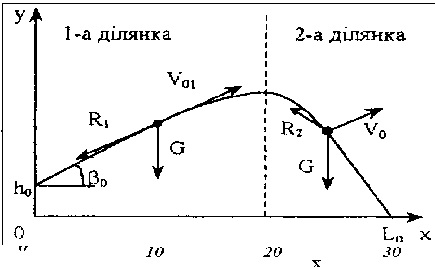
Рис.1.8 - Схема руху одиничної частки вогнегасної речовини
На різних ділянках траєкторія руху порошкової частки в проекціях на осі координат описується системами рівнянь:
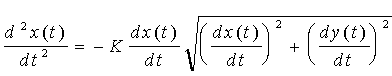 ; (1.23) ; (1.23)
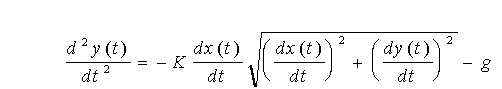
та 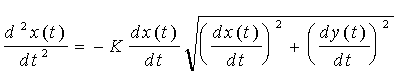 ; (1.24) ; (1.24)
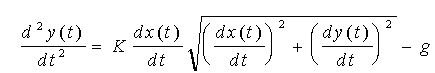
Початкові умови для рішення систем рівнянь (1.23) і (1.24), відповідно
q = b 0 p /180; x(0) = 0; y(0) = h0 ;
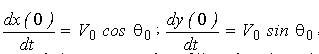 , (1.25) , (1.25)
та x(0) = xi ; y(0) = ymax 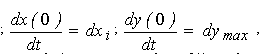 (1.26) (1.26)
де h0 - висота розташування імпульсного вогнегасника над рівнем земної поверхні, а коефіцієнт опору К визначається з виразу:
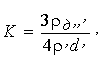 , (1.27) , (1.27)
у якому рг - щільність повітря;
рн, сн, - відповідно щільність і діаметр порошкової частки;
Сх - коефіцієнт аеродинамічного опору.
З урахуванням виразу (1.27), розв’язуючи спільно системи рівнянь (1.23) і (1.24) відносно х при у = 0, знаходять значення дальності подачі елементарної частки, оскільки Ln = х.
З розв’язання рівнянь (1.23) і (1.24) отримані кількісні оцінки впливу геометричних розмірів і щільності порошкових часток на дальність подачі частки (рис. 1.9).
а б
Рис. 1.9 - Залежність дальності подачі елементарнох частки
а) від кута нахилу ствола; б) від її початкової швидкості
Аналіз отриманих моделей показав, що визначальний вплив на дальність подачі частки буде справляти її початкова швидкість, максимальні значення дальності подачі досягаються в діапазоні початкових швидкостей (38-46) м/с і при кутах нахилу імпульсного вогнегасника, що знаходяться у діапазоні 5-10 градусів, а також те, що в діапазоні 0,5 - 1,5 м висота підйому імпульсного вогнегасника над рівнем землі практично не впливає на дальність подачі частки вогнегасної речовини.
У роботі Шаповалової О.О. [4] оцінювання параметрів руху розпорошеного потоку вогнегасної речовини відбувалося з застосуванням методу руху ізольованої краплі.
Рівняння записувалися в рамках таких допущень: рух розпорошеного струму рідини представлявся як політ крапель однакового розміру, що не взаємодіють між собою, з ідентичними траєкторіями; при витіканні з високою швидкістю струм розпадається безупинно поблизу сопла, перетворюючись на хмару розпорошеної рідини; розмір крапель зменшується на ділянці доставки їх до вогнища за рахунок природного випару; крапля до моменту контакту з фронтом полум'я зберігає половину свого початкового розміру; на краплю діють реактивна сила, сила опору середовища і сила ваги.
Система рівнянь, що описує рух одиночної краплі, має такий вид:
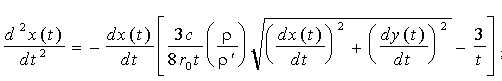 ; (1.28) ; (1.28)
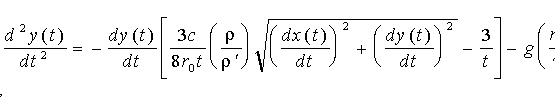 , ,
де с - аеродинамічний коефіцієнт; t = 1 - t g /r0 - безрозмірна змінна;
t - час, с;
r і r ` - щільності середовища і вогнегасної рідини відповідно, кг/м3, r0 - початкове значення радіуса краплі, м;
g - швидкість зменшення радіуса краплі, постійна для даної вогнегасної речовини, м/с;
g - прискорення руху вільного падіння, м/с2;
х, у - декартові координати, м.
Розв’язання цієї системи з використанням розкладання в ряд Тейлора до другого члена ряду для 0.5 < t < 1, що відповідає 0 <.t <g /r0 , дозволили одержати залежності дальності польоту краплі від початкової швидкості краплі і від фізичних характеристик рідини, радіуса крапель:
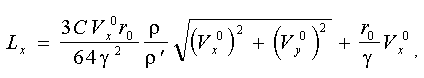 , (1.29) , (1.29)
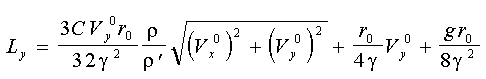 , (1.30) , (1.30)
причому  , ,  - початкові значення горизонтальної і вертикальної складової швидкості на зрізі, м/с; - початкові значення горизонтальної і вертикальної складової швидкості на зрізі, м/с;
Lx , Lу - горизонтальна і вертикальна складова дальності польоту краплі, м.
В роботі [4] показано, що залежність дальності подачі вогнегасної речовини від швидкості витікання ріди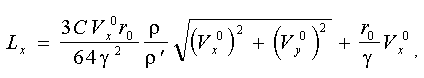 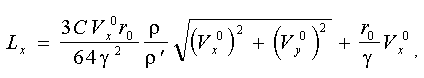 ни із сопла пожежного ствола має практично лінійний характер (рис.1.10). Це дозволило достатньо коректно перейти від максимальної дальності подачі як критерію оптимізації до максимальної швидкості на зрізі, і від розгляду фізичних процесів на ділянці доставки до гідродинамічних процесів усередині пожежного ствола. ни із сопла пожежного ствола має практично лінійний характер (рис.1.10). Це дозволило достатньо коректно перейти від максимальної дальності подачі як критерію оптимізації до максимальної швидкості на зрізі, і від розгляду фізичних процесів на ділянці доставки до гідродинамічних процесів усередині пожежного ствола.
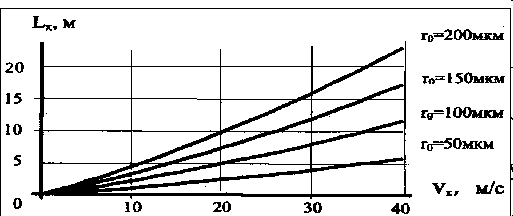
Рис. 1.10 - Залежність дальності польоту Lx від швидкості на вильоті Vx° при різноманітних значень радіуса краплі r0, g = 0.005 м/с
|