РОЗДІЛ 5. Оцінка теплового потоку від факелу полум’я до фігури площини
Рис. 5.1 - Схема розташування елементів теплообміну
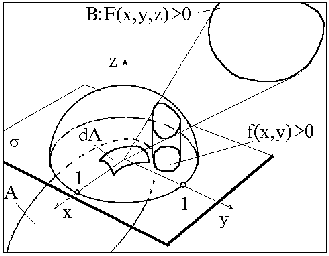
На рис. 5.1 зображено схему передачі тепла від випромінюючої поверхні А до сприймаючої поверхні В. Виберемо на поверхнях А і В елементарні ділянки dА і dВ. Позначимо через a і b гострі кути між нормалями до ділянок dA і dВ та напрямом випромінювання, а через r - відстань між центральними точками M і N ділянок dА і dВ відповідно.
Як відомо, відношення потоку випромінювання, що виходить з ділянки dA і падає на поверхню В, до всього потоку, який випромінюється ділянкою dA у півсферу, зветься локальним кутовим коефіцієнтом випромінювання (ККВ) і дорівнює значенню інтеграла:
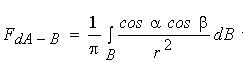. (5.1)
Для обчислення локальних ККВ зручно застосовувати метод сфери одиничного радіуса. Для пояснення суті методу оберемо площину s , що є дотичною до елемента dA і проходить через його центральну точку (рис. 5.2). З цієї ж точки будуємо півсферу радіуса 1, що спирається на площину s . З центра півсфери на її поверхню радіально проеціюємо поверхню В. Одержану радіальну проекцію поверхні В паралельно і ортогонально спроеціюємо на дотичну площину s . В результаті одержимо радіально-паралельну проекцію поверхні В (скорочено RP-проекцію В).
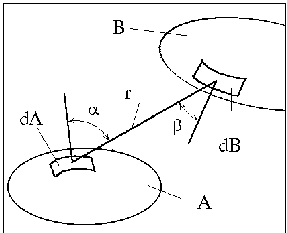
Рис. 5.2. Метод сфери радіуса 1
Значення локального ККВ дорівнює відношенню площі RP-проекції поверхні В до площі кола “екватора” сфери радіуса 1.
В роботах [В.М.Попова] оцінка площі RP-проекції здійснюється за допомогою опису RP-проекції поверхні В у вигляді нерівності f(x,y) > 0. Для цього площина Oxy суміщається з площиною s , а вісь Oz направляється у напрямі зовнішньої нормалі до елемента dA (рис. 5.2). Тоді, враховуючи знак функції f(x,y), засобами комп’ютерної графіки будується растрове зображення RP-проекції. Наближене значення локального ККВ дорівнює відношенню кількості растрових точок, що складають зображення RP-проекції та кола одиничного радіуса.
Наведений алгоритм має ряд недоліків, головним серед яких є необхідність обирати дрібний крок растра, в залежності від положення віддаленого і малого за розмірами об’єкта В. Тому подальші зусилля було направлено на точне обчислення площі RP-проекції. На хід міркувань не вплине те, що центральна точка елемента dA буде збігатися з початком координат, а дотична площина - з площиною 0xy. Тому рівняння півсфери радіуса 1 можна записати у вигляді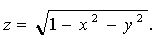 
Необхідно вказати алгоритм побудови функції f(x,y), щоб рівняння RP-проекції поверхні В мало вигляд f(x,y) = 0.
Легко перевірити, що коли поверхня В: F(x, y, z) = 0 має спільні точки з півсферою одиничного радіуса, то RP-проекцію лінії перетину вказаних поверхонь можна описати рівнянням F(x, y,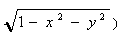 
= 0.
Нехай поверхня В “вироджується” у фігуру, що задана на довільній площині рівня відносно координатних площин.
Твердження. Якщо фігура В задана на площині рівня x = xp рівнянням F(y, z) = 0, то рівняння її RP-проекції має вид:
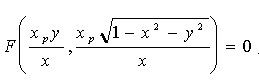. (5.2)
Приклад. Якщо еліпс 
задано на площині рівня x = p, то опис його RP-проекції має вид:
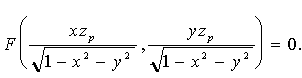(5.4)
Приклад. Якщо еліпс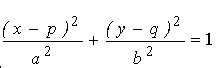 
задано на площині рівня z = w, то опис його RP-проекції має вид:
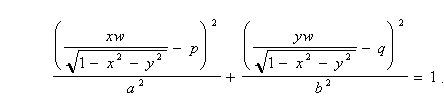. (5.5)
Далі розглянемо метод опису RP- проекції поверхонь другого порядку. Метод складається з двох етапів. Спочатку будується рівняння конуса з вершиною на початку координат, який огортає поверхню другого порядку. Потім визначається опис RP-проекції як проекції на координатну площину перетину зазначеного конуса з півсферою одиничного радіуса.
Твердження. Якщо рівняння поверхні другого порядку позначити
P(x, y, z) = a11x2 + a22y2+ a33z2 + 2a12xy + 2a13xz+ 2a23yz + 2a1x +2a2y +2a3z +a,
то рівняння конуса, який її огортає, при x0 = y0 = z0 = 0 має вид:
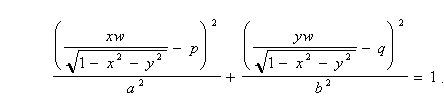(5.6)
Твердження. Рівняння RP-проекції поверхні другого порядку
P(x, y, z) = 0 має вид [98]:
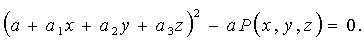(5.7)
Зазначимо, що рівняння (5.7) одержано за умови, що у рівняння (5.6) замість змінної z підставлено вираз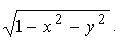 
.
Твердження. Рівняння RP-проекції сфери (рис. 5.3) з радіусом r і з центром у точці (a, b, c) має вид:
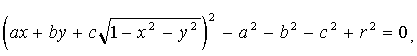, (5.8)
де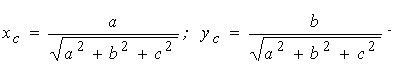 
- координати RP-проекції центра.
|
|
|
|
Рис. 5.3 - Схема променевого теплообміну між сферою і елементарною площадкою |
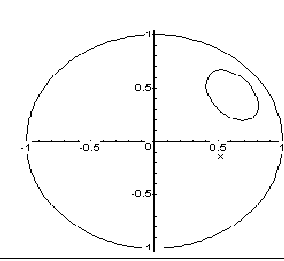
Рис. 5.4 - RP-проекція сфери та коло одиничного радіуса |
На рис. 5.4 наведено зображення RP-проекції сфери, яке побудовано за допомогою формули (5.8) і складеної Maple-програми, що наведено нижче.
restart: with (plots):
a:=7.: b:= 5.: c:= 7.: r:=3.:
f:=(a*x+b*y+c*sqrt(1.-x^2-y^2))^2-a^2-b^2-c^2+r^2;
s1:=implicitplot(f(x,y),x=-1..1,y=-1..1, color=0):
s2:=implicitplot(x^2 + y^2 = 1,x=-1..1,y=-1..1):
display(s1,s2);
Твердження. Рівняння конуса з вершиною у точці M(x0, y0, z0), який огортає зовні еліпсоїд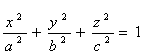 
, має вид:
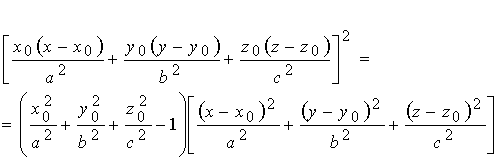(5.9)
Твердження. Рівняння конуса з вершиною у точці O(0, 0, 0), який огортає зовні еліпсоїд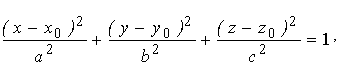 
, має вид:
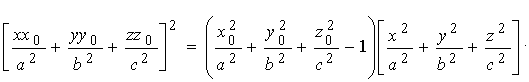. (5.10)
Твердження. Для еліпсоїда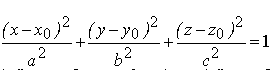 
рівняння його RP-проекції має вид
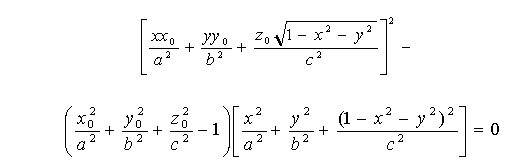. (5.11)
Далі розглянемо варіант побудови RP-проекції еліпса як плоскої фігури (рис. 5.5).
Рис. 5.5 - Схема променевого теплообміну між еліпсом
та перпендикулярною елементарною площадкою
Твердження. Рівняння RP-проекції еліпса має вид:
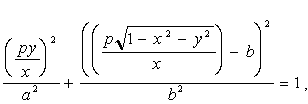, (5.12)
або, після очевидних перетворень, маємо
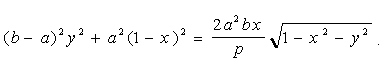. (5.13)
Для інтегрування необхідно з (5.13) вилучити змінну y. Після перетворень маємо
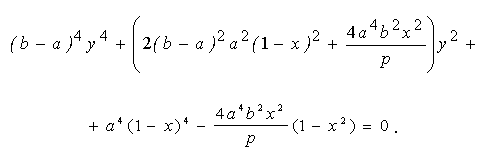. (5.14)
Розв’язавши квадратне рівняння (1.24) відносно y2, одержуємо:
, (5.15)
де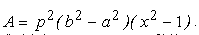 
. Проміжок інтегрування по змінній х визначається в результаті розв’язання відносно х рівняння y*(x) = 0:
.
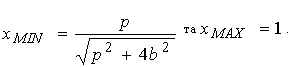(5.16)
Для визначення локального ККВ необхідно обчислити інтеграл:
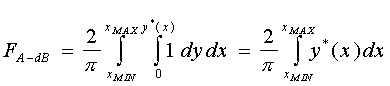. (5.17)
Формула (5.17) є основною для обчислення локальних ККВ, коли фігурою, що випромінює тепло, є еліпс (тобто осьовий перетин еліпсоїда).
Аналогічні формули знайдено і для випадку еліпсоїда.
Твердження. Якщо рівняння RP-проекції еліпса розв’яжемо відносно змінної y, то одержимо опис частини RP-проекції у виді:
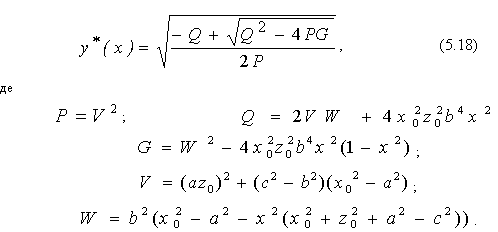
Для визначення локального ККВ необхідно обчислити інтеграл
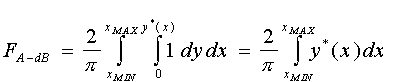. (5.19)
Формула (5.19) є основною для обчислення локальних ККВ, коли фігурою, що випромінює тепло, є еліпсоїд.
На рис. 5.6 наведено програму побудови RP-проекції та обчислення локального ККВ для еліпсоїда.
|
a := 5.: b:=5.: c :=70:
x0 := 50.: y0 := 0.: z0 := 75.:
ELPS := (x,y,z) -> 1.=((x-x0)/a)^2 +
((y-y0)/b)^2 + ((z-z0)/c)^2:
KONUS := (x*x0/a^2+y*y0/b^2+z*z0/c^2)^2 -
( ( (x0/a)^2+(y0/b)^2+(z0/c)^2-1. )*
( (x/a)^2 +(y/b)^2 +(z/c)^2 ) ):
f:=subs(z=sqrt(1 - x^2 - y^2),KONUS):
A1 := (a*z0)^2+(a*b)^2+(x0*c)^2-(x0*b)^2-(a*c)^2:
B1 := (x0*b)^2-(x0*x*b)^2+(z0*x*b)^2+
(x*a*b)^2 -(x*c*b)^2-(a*b)^2:
P1 := A1^2: Q1 := 2.*A1*B1+4.*z0^2*x0^2*b^4*x^2:
G1 := B1^2-4.*z0^2*x0^2*b^4*x^2*(1.-x^2):
y1 := sqrt((-Q1+sqrt(Q1^2-4.*P1*G1))/(2.*P1)):
sol := fsolve({y1},{x},0..x0/sqrt(x0^2+z0^2)):
x1 := evalf(subs(sol[1],x));
sol := fsolve({y1},{x},x0/sqrt(x0^2+z0^2)..1):
x2 := evalf(subs(sol[1],x));
p11 := plot(y1,x=x1..x2): p12 := plot(-y1,x=x1..x2):
display({p11,p12},scaling=CONSTRAINED,axes=BOXED);
simplify(int(1,y=0..y1)):
rab:= evalf(Int(%,x=x1..x2, 10)):
luki := Re(evalf(2.*rab/Pi));
|
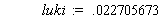
Рис. 5.6 - Програма обчислення локального ККВ для еліпсоїда