|
|
Cутність методу іміджевої екстраполяції полягає у розробці алгоритму (на базі алгоритму “інтерполяційного”) для відшукання (прогнозування) значення функції в деякій точці за межами доступного інтервалу визначення цієї функції за її значеннями у вузлових точках інтервалу. При цьому у словосполучення “значення функції” вкладено поняття “коренні функції”, тобто це множина точок, в яких функція приймає нульове значення, а також поняття, що екстрапольована точка розташована від доступного інтервалу на відстані не більшій, ніж максимальний крок дискретизації цього інтервалу.
Поліноміальна іміджева екстраполяція. Нехай на площині, де маємо декартову систему координат Oxy, рівняннями {Fi (x, y) = 0} (i = 1...N) в умовні моменти часу {t = ti} задана послідовність “концентричних” ліній, які не перетинають одна одну. Тобто для послідовності множин {Gi : Fi (x, y) ³ 0} нехай виконуються співвідношення G1 Ì G2 Ì ... Ì GN-1 Ì GN . Оберемо момент часу t = tN+1 за межами доступного інтервалу [t1 ... tN], тобто tN < tN+1 , при чому tN+1 - tN £ max (ti+1 - ti ), де i = 1...N.
Твердження. Рівняння сім’ї екстрапольованих ліній має вид:
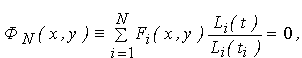 (6.24) (6.24)
де Li (t) = (t - t1) ... (t - ti - 1)(t - ti + 1) ... (t -tN).
Твердження. Рівняння екстрапольованої для моменту часу t = tN+1 лінії, має вид:
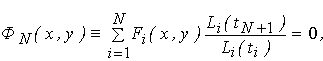 (6.25) (6.25)
де Li (t) = (t - t1) ... (t - ti - 1)(t - ti + 1) ... (t -tN).
Найпростішим видом формули (6.25) є лінійна іміджева екстраполяція, в основі якої лежить апроксимація кривої на ділянці між точками (tk, tk) і (tk+1, tk+1) прямою, що проходить через ці точки.
У результаті маємо опис сім’ї ліній, які здійснюють екстраполяцію за вузловими лініями Fk (x, y) = 0 i Fk+1 (x, y) = 0 в моменти часу t = tk i t = tk+1
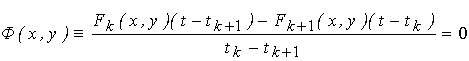 . (6.26) . (6.26)
Тобто за допомогою формули (6.26) можна знайти опис лінії для будь-якого значення t як в інтервалі [tk, tk+1], так і за його межами.
Конкретно при t = tk+2 з (6.26) маємо опис екстрапольованої лінії:
 . (6.27) . (6.27)
У випадку однакового кроку розбиття інтервалу D = tk+1 - tk = tk+2 - tk+1 з (6.27) маємо опис екстрапольованої кривої Ф (x, y) º 2 Fk+1 (x, y) - Fk (x, y)=0.
При N=3 з виразу (6.25) можна одержати “трилінійну” екстраполяційну формулу для трьох точок t = t1, t = t2 та t = t3 і для трьох ліній, описаних відповідними рівняннями F1 (x, y) = 0, F2 (x, y) = 0 і F3 (x, y) = 0.
Твердження. Трилінійне рівняння екстраполяційної лінії для моменту часу t = t4 за умови рівномірного розбиття інтервалу має вид:
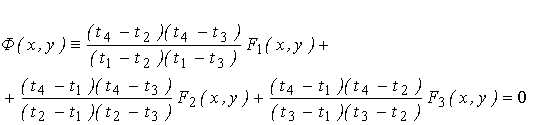 (6.28) (6.28)
Наприклад, для точок з координатами t1 = 1; t2 = 2 і t3 = 3 t4 = 4 маємо:
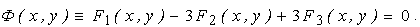 . (6.29) . (6.29)
Таким чином, щойно було показано, до чого зводиться екстраполяція засобами поліноміальної інтерполяції. Аналогічне можна було б показати і у випадку сплайн-інтерполяції. До недоліків згаданих методів слід віднести те, що при складанні алгоритму екстраполіція не враховується “внесок” у зміну форми екстрапольованої кривої, який здійснюють окремі вузлові елементи. Це удалося розв’язати за допомогою векторної екстраполяції.
Побудова екстраполяційної формули на векторній основі. Нехай в точках xi задано відповідні значення функції yi (i = 1...N). Задача “поточкової” екстраполяції полягає у визначенні значення функції yN+1 в точці xN+1, яка знаходиться за межами інтервалу [x1...xN]. Традиційно цю задачу розв’язують за допомогою інтерполяційних формул (Лагранжа, сплайнів). Але, як було показано на реальних прикладах в пп. 3.1 і 3.2, згаданим формулам притаманні певні недоліки, які випливають з їх поліноміальної структури. Тому побудову екстраполяційних формул здійснимо на векторній основі.
Для визначення функції за межами доступного інтервалу [x1...xN] виберемо послідовність векторів qi, що сполучають точки з координатами (xi, yi) i (xi+1, yi+1), де i = 1...N-1 (рис. 6.17).
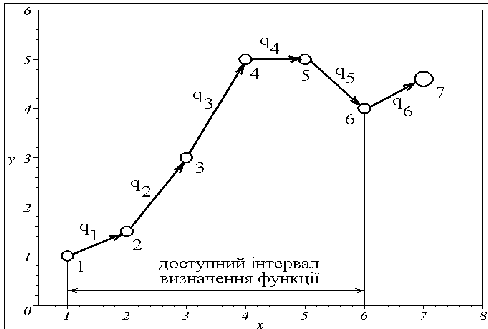
Рис. 6.17 - Схема визначення векторної екстраполяції
За допомогою цієї послідовності визначимо результуючий вектор як суму 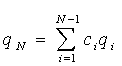 , де сi - вагові коефіцієнти, що вказують “вагу” впливу на екстраполяційний процес попередніх варіацій значень функції. Координати вектора qN дозволяють скласти рівняння відрізка, що сполучає точки з координатами {(xN, yN) ¾ (xN+1, yN+1), }; звідки маємо вираз для обчислення значення yN+1 даної функції в точці xN+1: , де сi - вагові коефіцієнти, що вказують “вагу” впливу на екстраполяційний процес попередніх варіацій значень функції. Координати вектора qN дозволяють скласти рівняння відрізка, що сполучає точки з координатами {(xN, yN) ¾ (xN+1, yN+1), }; звідки маємо вираз для обчислення значення yN+1 даної функції в точці xN+1:
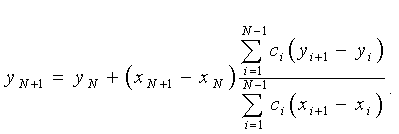 . (6.30) . (6.30)
У залежності від вибору величин сі (і = 1...N-1), одержуємо різновиди екстраполяцій. Так, коли необхідно, щоб при формуванні значення yN+1 на цей процес впливали однаково всі попередні варіації значень yi , то необхідно обрати сі = 1. Якщо необхідно перевагу віддати варіаціям значень функції з правої частини інтервалу [x1...xN], то в якості сі необхідно обрати якусь зростаючу функцію, наприклад степеневу сі = i k (де k - ціле додатнє число). Коли ж переважати повинні варіації значень функції з лівої частини інтервалу [x1 ... xN], то в якості сі необхідно обрати якусь спадаючу функцію, наприклад, також степеневу сі = i k (де k - ціле від’ємне число). Значення показника степеня k пропонується обрати у якості регулюючого параметра екстраполяції.
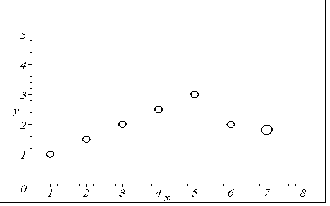
Приклад 1. Нехай п’ять точок деякої функції розташовано за лінійним законом, а шоста (остання) точка нехай імітує “викид”.
Було складено Maple-програму, що реалізує векторну екстраполяцію.
|
restart: with(plots):with(plottools): N := 6: k :=-2:
xx[1] := 1: yy[1] := 1: xx[2] := 2: yy[2] := 2.5:
xx[3] := 3: yy[3] := 2: xx[4] := 4: yy[4] := 2.5:
xx[5] := 5: yy[5] := 3: xx[6] := 6: yy[6] := 2:
for i from 1 to N do
pnt[i] := circle([xx[i],yy[i]], 0.15, color=black,
scaling=CONSTRAINED, thickness=3):
end do: # i
a := 0: b := 0:
for i from 1 to N-1 do
a := a + i^k*(xx[i+1] - xx[i]);
b := b + i^k*(yy[i+1] - yy[i]);
end do: # i
yy[N+1] := (xx[N+1] - xx[N])*b/a + yy[N]:
pntN1 := circle([xx[N+1],yy[N+1]], 0.2, color= blue,
scaling=CONSTRAINED, thickness=3):
display({seq(pnt[i],i=1..N), pntN1},
scaling=CONSTRAINED, axes=boxed, view=[0..N+2, 0..5]); |
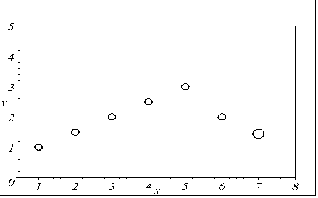
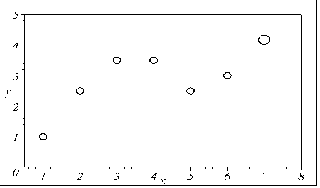
У результаті виконання програми екстраполяції за формулою (6.30) маємо варіанти положення сьомої точки в залежності від значення k (рис. 6.18). Це положення вказує на тенденцію "поведінки" функції за межами доступного інтервалу [1...6]. На рис 6.18 а зображено випадок, коли варіації всіх попередніх точок однаково впливають на формування положення сьомої точки. Коли ж переважають варіації точок правої частини інтервалу (де наявний “зрив” лінійності), то маємо такі зображення, як на рис. 6.18 б та рис. 6.18 в. При цьому останній випадок більше залежить від згаданого зриву. І, нарешті, на рис. 6.18 г показано випадок, коли при формуванні положення сьомої точки переважає вплив варіації точок, які знаходяться на лівому кінці інтервалу.
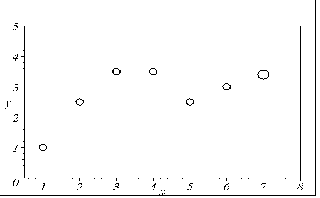
Приклад 2. Нехай п’ять точок деякої функції розташовано за “параболічним” законом, а шоста (остання) точка нехай знову імітує “викид”. У результаті екстраполяції за формулою (6.30) одержимо варіанти положення сьомої точки в залежності від значення k (рис. 6.19).
Аналіз наведених зображень також переконує у тому, що за допомогою формули (6.30) можна здійснити екстраполяцію і нелінійної функції з урахуванням степеня впливу на кінцевий результат варіацій певної групи точок з доступного інтервалу її зміни.
|

|
|
|
а) k = 0; |
б) k = 2; |
|
|
|
|
в) k = 5; |
г) k = -2. |
Рис. 6.18 - Схема визначення значення “лінійної” функції
за межами
доступного інтервалу в залежності від параметра екстраполяції
Використання векторної екстраполяції для визначення кромок вигоряння за межами доступного часового інтервалу. Формулу (6.30) використаємо для опису прогнозованих кромок вигоряння.
Твердження. Нехай маємо N рівнянь {Fi (x, y) = 0}, які є описом послідовності вузлових кромок вигоряння в моменти часу t = ti. Тоді екстрапольовану криву в момент часу t = tN можна описати рівнянням:
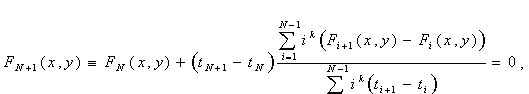 , (6.31) , (6.31)
де k - регулюючий параметр екстраполяції.
|
|

|
|
а) k = 0; |
б) k = 2; |
|
|
|
|
в) k = 5; |
г) k = - 2. |
Рис. 6.19 - Схема визначення значення “параболічної” функції
за межами доступного інтервалу
в залежності від параметра екстраполяції
Приклад (тестовий) . Нехай маємо чотири абстрактні вузлові контури вигоряння (наприклад, коло та три квадрати), які в умовні моменти часу t1 = 1, t2 = 2, t3 = 3 та t4 = 4 описані рівняннями:
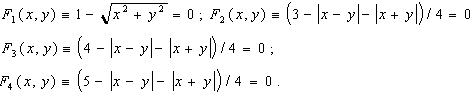 (6.32) (6.32)
Складено Maple- програму іміджевої екстраполяції.
|
restart: with(plots): k := - 2:
f1 := 1 - sqrt(x^2 + y^2):
f2 := (3 - abs(x-y) - abs(x+y))/2:
f3 := (4 - abs(x-y) - abs(x+y))/2:
f4 := (5 - abs(x-y) - abs(x+y))/2:
f5 := f4 + ((f2 - f1)*1^k + (f3 - f2)*2^k +
(f4 - f3)*3^k)/(1^k+2^k+3^k);
implicitplot({f1,f2,f3,f4,f5},x=-5..5,y=-5..5,
axes=BOXED, grid=[100,100], scaling=CONSTRAINED); |
У результаті одержуємо рівняння екстраполяційної кривої на момент часу t5 = 5:
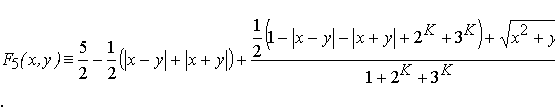 . .
(6.33)
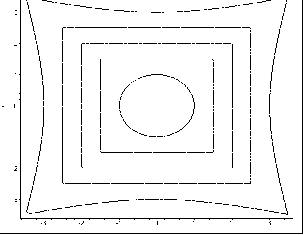
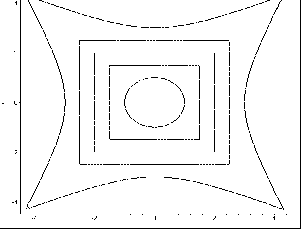
На рис. 6.20 наведено зображення екстраполяційної кромки вигоряння (зовнішня лінія) в залежності від вузлових кромок вигоряння та значення k.
При цьому, варіанту k = -2 відповідає випадок, коли на екстраполяційну кромку переважає вплив варіації форми кривих “коло - внутрішній квадрат”, що характерно для початкової фази лісової пожежі.
Варіанту k = 2 відповідає випадок, коли на екстраполяційну кромку переважає вплив тенденції зміни форми зовнішніх квадратів - це відображає прикінцеву фазу лісової пожежі.
|

|
|
|
а) k = 0;
|
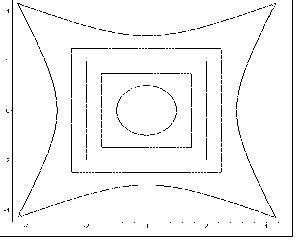
б) k = 2;
|
|
|
|
|
в) k = -2; |
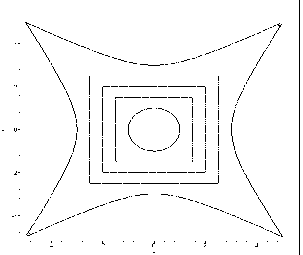
г) k = - 5. |
Рис. 6.20 - Екстраполяційні криві в залежності
від параметра екстраполяції
Тобто для тестового прикладу має місце таке спостереження - від’ємні значення k при екстраполяції за формулою (6.33) відповідають початковій фазі пожежі (при цьому “відчувається” вплив зміни форми кола на квадрат), а додатні значення k відповідають її прикінцевій фазі.
|