|
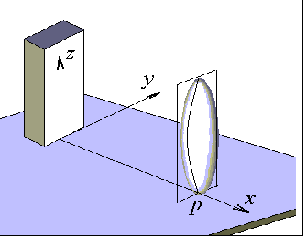
З метою складання більш ефективних алгоритмів обчислення локальних ККВ? доцільно застосувати наступний прийом. Будемо вважати, що тепловий потік, який надходить від поверхні факела полум’я до поверхні теплоприймача (рис. 5.16), мало відрізняється від теплового потоку, який надходить від абстрактного осьового перетину поверхні факела полум’я (на рис. 5. 17 зображено перетин площиною x = p). Таке припущення дозволить спростити математичне забезпечення відповідних алгоритмів.
|
|
|
|
Рис. 5.16 - Взаємне положення факела і теплоприймача |
|
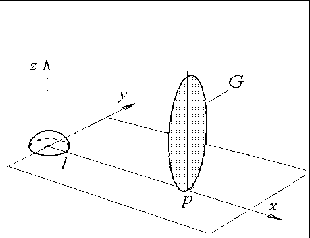
Рис. 5.17 - Осьовий перетин факела і сфера радіуса 1 | |
Для реалізації зазначеного підходу необхідно розробити метод опису RP-проекції осьового перетину. Але спочатку необхідно описати сам осьовий перетин. Для цього доцільно застосувати полярні координати.
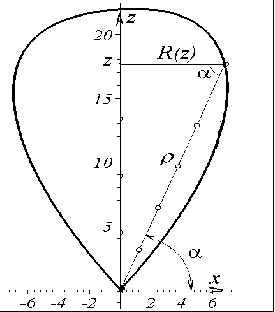
Наведемо формули зв’язку між декартовими і полярними координатами 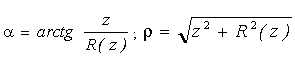 (рис. 5.18). При цьому здійснюється перехід від системи координат “висота факела – радіус факела” до системи координат “полярний кут – полярний радіус”. На рис. 5.19 у якості прикладу наведено зображення осьового перетину, який при значеннях кута 0,9 £ a £ 2,24 описано полярним рівнянням: (рис. 5.18). При цьому здійснюється перехід від системи координат “висота факела – радіус факела” до системи координат “полярний кут – полярний радіус”. На рис. 5.19 у якості прикладу наведено зображення осьового перетину, який при значеннях кута 0,9 £ a £ 2,24 описано полярним рівнянням:
 (5.20) (5.20)
|
|
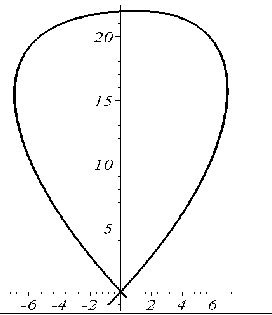
|
|
Рис. 5.18 - Зв’язок між системами координат |
Рис. 5.19 - Зображення осьового перетину факела |
Твердження. Нехай R = R(a ) є полярним рівнянням осевого перетину, що розташовано на площині рівня x = p. Тоді описом його RP-проекції будуть вирази:
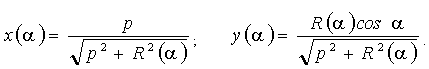 . (5.21) . (5.21)
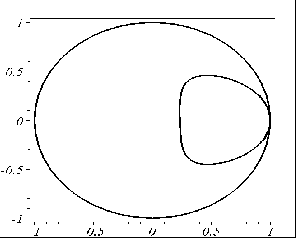
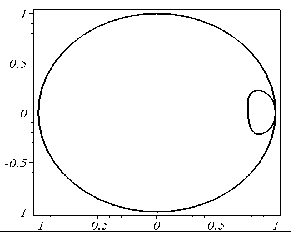
На рис. 5.20 наведено програму побудови RP-проекції осьового перетину у залежності від відстані p. На рис. 5.21 наведено приклади виконання програми для різних значень p.
Рис. 5.20 - Програма побудови RP-проекції осьового перетину
|
|

|
|
P = 5 |
P = 10 |
|
|
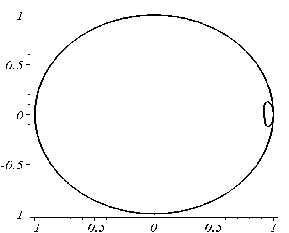
|
|
P = 25 |
P = 50 |
Рис. 5.21 - Приклади виконання програми для різних значень p
Складена програма дозволяє одержати аналітичний опис RP-проекції осьового перетину.
Твердження . Аналітичний опис RP-проекції осьового перетину при p = 10 (як приклад) має вид:
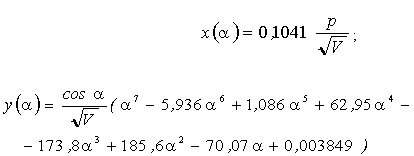
, (5.22)
де
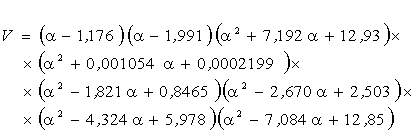 . .
Аналогічні результати можна одержати і у випадку, коли осьовий перетин розташований у площині рівня z = q. Це буде тоді, коли теплоприймач розташовано паралельно осі обертання факела полум’я.
Твердження. Нехай R = R(a ) є полярним рівнянням осьового перетину, що розташовано на площині рівня z = q, причому полюс має координати (x0, y0). Тоді описом RP-проекції осьового перетину будуть вирази:
; (5.23)
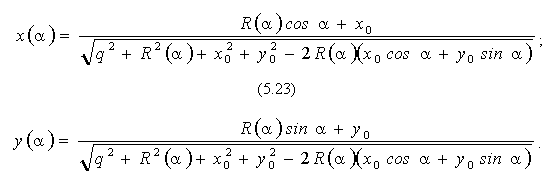
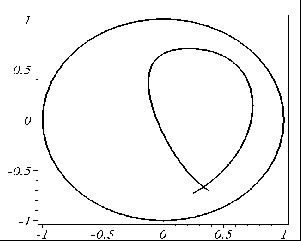
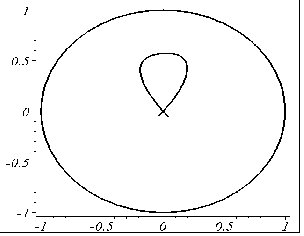
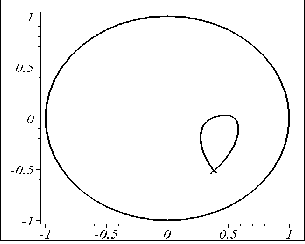
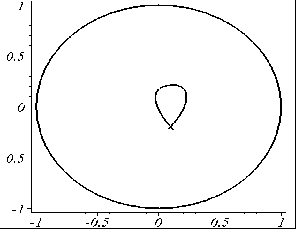
На рис. 5.22 наведено програму аналітичного опису та побудови зображень RP-проекції для розглянутого випадку. На рис. 5.23 наведено приклади виконання програми.
|
q := 10: x0 := 5: y0 := -10:
R := a -> 9.608*a^7-57.022*a^6+10.43*a^5+604.7*a^4-
1670.*a^3+1783.*a^2-673.1*a+.03697:
x := R(a)*cos(a) + x0: y := R(a)*sin(a) + y0:
znam := sqrt(x^2 + y^2 + q^2):
xrp := evalf(factor(simplify(x / znam)),4);
|
Рис. 5.22 - Програма аналітичного опису та побудови зображень RP-проекції
|
|
|
|
q=10: x0=5: y0=-10: |
q=30: x0=0: y0=0: |
|
|
|
|
q=30: x0=15: y0=-20: |
q=50: x0=5: y0=-10: |
Рис. 5.23 - Приклади виконання програми
|