|
|
Як було вже зазначено вище, повне визначення результату зіткнення двох часток (визначення кута х) вимагає рішення рівнянь руху з урахуванням конкретного закону взаємодії часток.
Відповідно до загального правила, будемо розглядати спочатку еквівалентну задачу про відхилення однієї частки з масою т у поле U(r) нерухомого силового центра (розташованого в центрі інерції часток).
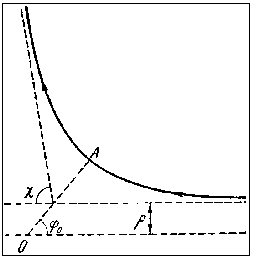
Рис. 4.10 - Трек розсіяння
Траєкторія частки в центральному полі симетрична стосовно прямої, проведеної в найближчу до центра точку орбіти ( ОА на рис. 4.10). Тому обидві асимптоти орбіти перетинають зазначену пряму під однаковими кутами. Якщо позначити ці кути за допомогою j 0, то кут c відхилення частки при її прольоті повз центр є, як видно з рисунка,
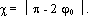 . (4.21) . (4.21)
Кут же j 0 визначається згідно (4.7) інтегралом:
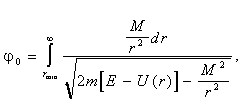
(4.22)
узятим між найближчим до центра і нескінченно віддаленим положенням частки. Нагадаємо, що rmin є коренем виразу, що знаходиться під знаком радикала.
При і нфінітному русі, з яким ми маємо тут справу, зручно ввести замість постійних Е і М інші - швидкість v¥ частки на нескінченності і так звану прицільну відстань r . Останнє являє собою довжину перпендикуляра, опущеного з центра на напрямок v¥ , тобто відстань, на якій частка пройшла б повз центр, якби силове поле було відсутнє (рис. 4.12). Енергія і момент виражаються через ці величини згідно
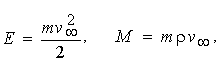 (4.23) (4.23)
а формула (4.22) приймає вид:
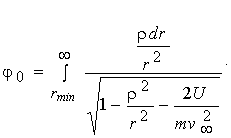 . (4.24) . (4.24)
Разом з (4.21) вона визначає залежність c від r .
У фізичних застосуваннях приходиться звичайно мати справу не з індивідуальним відхиленням частки, а, як говорять, з розсіюванням цілого пучка однакових часток, що падають на центр, що розсіює, з однаковою швидкістю v¥ . Різні частки в пучку володіють різними прицільними відстанями і відповідно розсіюються під різними кутами c . Позначимо за допомогою dN число часток, що розсіюються в одиницю часу на кути, що лежать в інтервалі між c i c + dc . Саме по собі це число незручне для характеристики процесу розсіювання, тому що воно залежить від щільності падаючого пучка (пропорційно їй). Тому введемо відношення
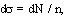 (4.25) (4.25)
де n - число часток, що проходять в одиницю часу через одиницю площі поперечного перерізу пучка (ми припускаємо, природно, що пучок однорідний по усьому своєму перетину). Це відношення має розмірність площі і називається ефективним перетином (чи просто перетином) розсіювання. Воно цілком визначається видом поля, що розсіює, і є найважливішою характеристикою процесу розсіювання.
Будемо вважати, що зв'язок між c і r - взаємно однозначний; це так, якщо кут розсіювання є монотонно спадаючою функцією прицільної відстані. У такому випадку розсіюються в заданий інтервал кутів між c і c + dc лише ті частки, що летять із прицільною відстанню у визначеному інтервалі між r (c ) і r (c ) + d r (c ). Число таких часток дорівнює добутку п на площу кільця між колами з радіусами r і r + dr , тобто dN = 2p r dr n. Тому ефективний перетин
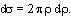 (4.26) (4.26)
Щоб знайти залежність ефективного перетину від кута розсіювання, досить переписати цей вираз у виді:
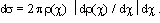 (4.27) (4.27)
Ми пишемо тут абсолютне значення похідної dr (c ) / dc , маючи на увазі, що вона може бути негативною (як це звичайно буває). Часто відносять ds не до елемента плоского кута dc , а до елемента тілесного кута do. Тілесний кут між конусами з кутами розчину c i c + dc є do = 2p sinc dc . Тому маємо з (4.27):
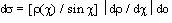 (4.28) (4.28)
Повертаючись до фактичної задачі про розсіювання пучка часток не на нерухомому силовому центрі, а на інших частках, які спочатку були нерухомими, ми можемо сказати, що формула (4.28) визначає ефективний перетин у залежності від кута розсіювання в системі центра інерції. При цьому виходять вирази як для перетину розсіювання падаючого пучка часток (c виражене через 6,), так і для часток, які спочатку були нерухомими (c виражене через 64).
Одне з найважливіших застосувань отриманих вище формул — розсіювання заряджених часток у кулонівському полі. Дійсно, поклавши в (4.24) U = a / r і роблячи елементарне інтегрування, одержимо:
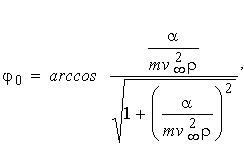 , ,
відкіля 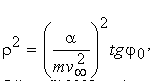 , або уводячи згідно (4.21) j 0 = , або уводячи згідно (4.21) j 0 = (p - c ) / 2:
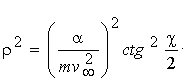 . (4.29) . (4.29)
Диференціюючи цей вираз по c і підставляючи в (4.27) чи в (4.28), одержимо:
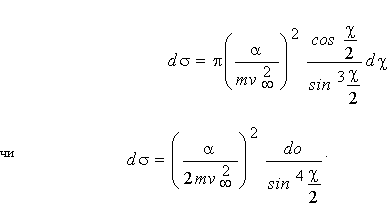 . (4.30) . (4.30)
Це так звана формула Резерфорда. Відзначимо, що ефективний перетин не залежить від знака a , тому отриманий результат відноситься в однаковій мірі до кулонівського поля відштовхування і притягання.
Далі нагадаємо [18] елементи теорії опису траєкторії переміщення першої частки в силовому полі другої (нерухомої) частки з потенціалом U = - k / r, де константа k > 0, якщо маємо випадок притягання часток, і k < 0 - у випадку відштовхування; r - радіус-вектор частки. Тоді рівняння руху першої частки має вид:
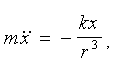 , (4.31) , (4.31)
де m - маса частки, x - координата переміщення.
Оскільки момент імпульсу частки визначається як 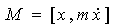 і являє собою постійний вектор, ми введемо ще один вектор Q, визначивши його в такий спосіб: і являє собою постійний вектор, ми введемо ще один вектор Q, визначивши його в такий спосіб: 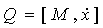 . .
Оскільки вектор Q перпендикулярний вектору М, то він лежить в орбітальній площині. Якщо взяти до уваги рівність 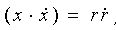 , що випливає з тотожності r2 = (х • х), то можна знайти вираз для похідної за часом від Q:
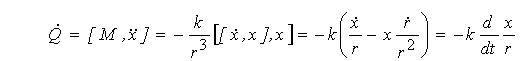
або
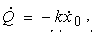 , (4.32) , (4.32)
де через x0 позначений одиничний вектор, спрямований уздовж радіуса-вектора x0 = х/r.
Рівняння (4.32) легко проінтегрувати; у результаті одержимо:
Q + k x0 = - B, (4.33)
де В — постійний вектор.
Склавши скалярний добуток на х0 обох частин рівності (4.33) і скориставшись перетворенням:
 , (4.34) , (4.34)
одержимо тотожність:
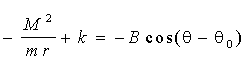 , (4.35) , (4.35)
причому В = ½ В½ ; тут передбачається, що вектор В утворить кут q 0 з віссю х (в орбітальній площині), а вектор x0 — кут q з тією ж віссю х.
Рівняння (4.35) описує траєкторію частки, що являє собою конічний перетин (для спрощення варто взяти В = АМ 2 / т).
Піднесемо до квадрату обидві частини рівності (4.33). Оскільки вектор М перпендикулярний 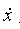 , ми одержимо, що Q2 дорівнює , ми одержимо, що Q2 дорівнює 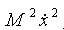 , отже , отже
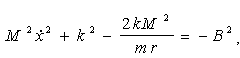 , (4.36) , (4.36)
де прийняті до уваги тотожності (4.34).
Рівняння (4.36) можна записати ще й у такому виді:
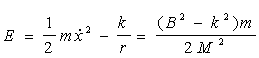 . (4.37) . (4.37)
Таким чином, ми одержали вираз для позначення енергії частки. З (4.37) видно, що якщо k позитивно, то знак Е, а значить і характер траєкторії визначається завбільшки (якщо ж k негативно, Е завжди позитивно, а траєкторія завжди буде гіперболою). Якщо B > k, то частка може піти на нескінченність з кінцевою швидкістю; ми маємо справу з гіперболою (крива 1 на рис. 4.11).
Підкреслимо , що отримано тільки одну з двох гілок гіперболи, оскільки r - істотно позитивна величина. Початок координат буде внутрішнім фокусом, якщо k > 0, і зовнішнім, якщо k <0.
Якщо B = k, то швидкість на нескінченності обертається в нуль, а траєкторією є парабола (крива 2). Якщо B < k, траєкторією буде еліпс (крива 3). Нарешті якщо В = 0, енергія досягає найменшого значення, сумісного з заданим значенням М, і траєкторія перетворюється в коло.
|
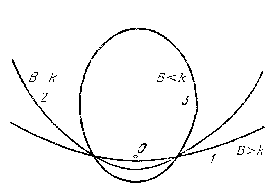
|
|
|
Рис. 4.11 - Можливі траєкторії часток із заданим моментом імпульсу (О-центр силового поля) |
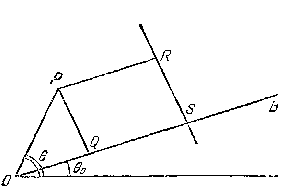
Рис. 4.12 - Геометричне місце точок Р є конічним перетином, якщо відношення½ OP½ до ½ PR½ постійно |
Скориставшись М 2 А/т = В і перетворивши тотожність (4.35) на
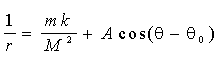 , (4.38) , (4.38)
ми виявляємо, що умови B > k, B = k і B < k відповідають варіантам відношення ½ ОР½ до ½ PR½ у формулі:
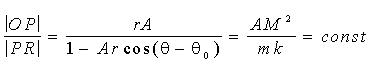 (4.39) (4.39)
як більшому, рівному і меншому одиниці. Що ще раз підтверджує класичні результати - ці умови відповідають гіперболічним, параболічним і еліптичним траєкторіям.
На рис. 4.12 довжина відрізка OS дорівнює А -1. При цьому легко помітити, що
½ OQ½ = r cos (q - q 0); ½ PR½ = [ 1 - Ar cos (q - q 0)] / A.
Вищевикладене переконує в тому, що буде безперспективним трасування потоку a - часток на основі отриманого опису конічних перетинів (4.38). При алгоритмічній реалізації це приведе до складного аналізу геометричної форми визначеної ділянки відповідного елемента треку.
|