|
|
Трасування струменя води будемо здійснювати за допомогою розв’язання системи диференціальних рівнянь:
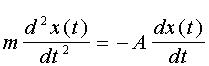 ; (1.31) ; (1.31)
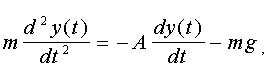 , ,
де А - коефіцієнт опору повітря;
massa - маса частки;
g - константа тяжіння.
Для виконання складених програм необхідно задати вхідні параметри: V0 - початкову швидкість частки води та alpha - кут вильоту цієї частки. Тоді початкові умови для розв’язання системи рівнянь матимуть вид:
x(0)=0, D(x)(0)=Vox, y(0)=0, D(y)(0)=Voy ,
де Vox := V0*cos(alpha): Voy := V0*sin(alpha):
В програмах передбачено для порівняння будувати траєкторію струменя води без урахуванням опору повітря (тобто опір повітря дорівнює нулю), а також з урахуванням опору повітря (наприклад, А = 0,1). Для цього для зручності використаємо вектор A := [0.1, 0].
На рис.1.11 наведено програму розрахунку траєкторії струменя із пожежного ствола з урахуванням опору повітря в залежності від кута, який вісь ствола утворює з горизонталлю.
В результаті виконання програми на диску С буде сформовано файл name.gif з кадрами анімаційного фільму траєкторії струменя води в залежності від кута, який вісь ствола утворює з горизонталлю.
V0 := 20: massa := 0.2:
A := [0.1, 0]: g:=9.8:
ramka := curve([[0,0], [50,0], [50,20], [0,20],[0,0]],
color=red, linestyle=3, thickness=2):
for i from 1 to 50 do
alpha := evalf(i*Pi/2/50):
alf := convert(evalf(360*alpha/2/Pi,2), string):
txt[i] := textplot({[40,18,"alpha = "], [47,18,`alf`]}, font=[TIMES,ROMAN,16]):
Vox := V0*cos(alpha): Voy := V0*sin(alpha):
sys1 := massa*diff(x(t),t$2)=-A[1]*diff(x(t),t),
massa*diff(y(t),t$2)=-A[1]*diff(y(t),t)-massa*g:
sys2 := massa*diff(x(t),t$2)=-A[2]*diff(x(t),t),
massa*diff(y(t),t$2)=-A[2]*diff(y(t),t)-massa*g:
p1 := dsolve({sys1, x(0)=0, D(x)(0)=Vox,
y(0)=0, D(y)(0)=Voy}, {y(t), x(t)},
type=numeric, output=listprocedure):
p2 := dsolve({sys2, x(0)=0, D(x)(0)=Vox,
y(0)=0, D(y)(0)=Voy}, {y(t), x(t)},
type=numeric, output=listprocedure):
a1 := odeplot(p1, [x(t), y(t)],
view=[0..50,0..25], thickness=3,numpoints=300):
a2 := odeplot(p2, [x(t), y(t)],
view=[0..50,0..25], thickness=3,numpoints=300):
Gr[i] := display({a1,a2,ramka,txt[i]},
scaling=CONSTRAINED,labels=[t,H], labelfont=[TIMES,BOLD,14],axesfont=[TIMES,ITALIC,16]);
end do:
for i from 1 by 5 while i < 50 do Gr[i]; od;
plotsetup(gif, plotoutput= `с:name.gif`);
display(seq(Gr[i],i=1..50), scaling=CONSTRAINED,
axes=NONE,insequence=true);
Рис. 1.11 - Програма побудови траєкторії струменя води в залежності від кута, який вісь ствола утворює з горизонталлю
На рис. 1.12 наведено приклади кадрів анімаційного фільму.
Рис. 1.12 - Приклади траєкторії струменя води в залежності
від кута нахилу
На рис.1.13 наведено програму розрахунку траєкторії струменя із пожежного ствола з урахуванням опору повітря, в залежності від маси елементарної частки води (тобто від витрачання води).
В результаті виконання програми на диску С буде сформовано файл name.gif з кадрами анімаційного фільму траєкторії струменя води, в залежності від маси елементарної частки води (тобто від витрачання води). На рис.1.14 наведено приклади кадрів траєкторії струменя із ствола.
restart: with(plots): with(plottools):
V0 := 20: A := [0.1, 0]: alpha := Pi/4: g:=9.8:
ramka := curve([[0,0],[50,0],[50,20],[0,20],[0,0]],
color=red, linestyle=3, thickness=2):
for i from 1 to 50 do
massa := evalf(2*i/50):
mas := convert(evalf(massa,2), string):
txt[i] := textplot({[40,18,"massa = "],
[47,18,`mas`]}, font=[TIMES,ROMAN,12]):
Vox := V0*cos(alpha): Voy := V0*sin(alpha):
sys1 := massa*diff(x(t),t$2)=-A[1]*diff(x(t),t),
massa*diff(y(t),t$2)=-A[1]*diff(y(t),t)-massa*g;
sys2 := massa*diff(x(t),t$2)=-A[2]*diff(x(t),t),
massa*diff(y(t),t$2)=-A[2]*diff(y(t),t)-massa*g;
p1 := dsolve({sys1, x(0)=0, D(x)(0)=Vox,
y(0)=0, D(y)(0)=Voy}, {y(t), x(t)},
type=numeric, output=listprocedure);
p2 := dsolve({sys2, x(0)=0, D(x)(0)=Vox,
y(0)=0, D(y)(0)=Voy}, {y(t), x(t)},
type=numeric, output=listprocedure);
a1 := odeplot(p1, [x(t), y(t)],
view=[0..50,0..25], thickness=3,numpoints=300):
a2 := odeplot(p2, [x(t), y(t)],
view=[0..50,0..25], thickness=3,numpoints=300):
Gr[i] := display({a1,a2,ramka,txt[i]},
scaling=CONSTRAINED,labels=[t,H], labelfont=[TIMES,BOLD,14],axesfont=[TIMES,ITALIC,14]);
end do:
for i from 1 by 5 while i < 50 do Gr[i]; od;
display(seq(Gr[i],i=1..50), scaling=CONSTRAINED,
axes=NONE,insequence=true);
plotsetup(gif, plotoutput= `c:name.gif`);
display(seq(Gr[i],i=1..50), scaling=CONSTRAINED,
axes=NONE,insequence=true);
Рис. 1.13 - Програма побудови траєкторії струменя води в залежності від витрачання води
Рис. 1.14 - Приклади зображення траєкторії струменя води в залежності від її витрачання w
|
|
|